Hur se injektivitet och surjektivitet i funktionen?

Hej!

Kan det var så att du låser dig till att $x$ måste vara heltal? Eller varför tänker du att 3 eller -3 inte kan nås? Funktionen är ett polynom (alltså kontinuerligt) som antingen går mot $\pm \infty$ beroende på riktning. Alla tal kommer nås. 

Även om det inte hjälper dig i en tentasituation kan man försäkra sig om detta genom att plotta grafen

.

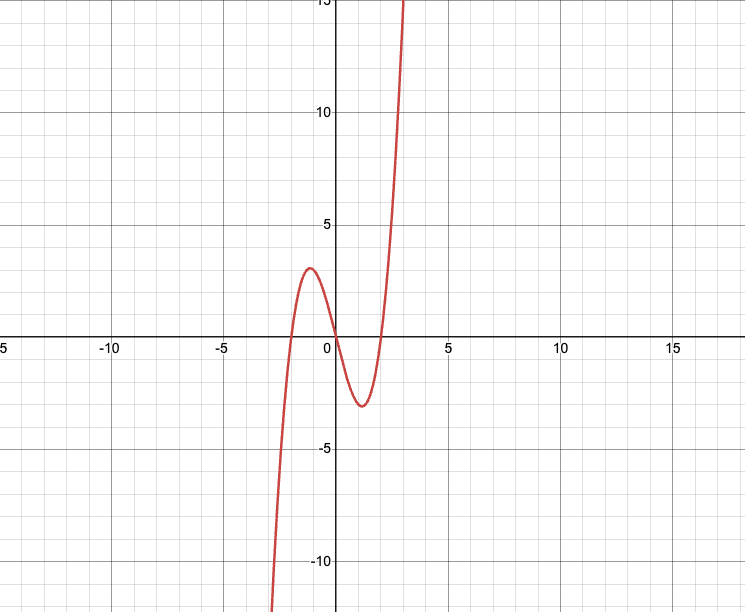MrPotatohead skrev:

Hej!

Kan det var så att du låser dig till att $x$ måste vara heltal. Eller varför tänker du att 3 eller -3 inte kan nås? Funktionen är ett polynom (alltså kontinuerligt) som antingen går mot $\pm \infty$ beroende på riktning. Alla tal kommer nås. 

Även om det inte hjälper dig i en tentasituation kan man försäkra sig om detta genom att plotta grafen

.

Aahh... Ja! Var fortfarande inne i talteori-tänket!

Tack för svaret! En lite dum fråga möjligen, men hur kan man förstå att tillägget med "-4x" inte orsakar några hopp i funktionen och att den fortfarande är surjektiv? (Om man tillfälligt ignorerar att alla polynom är kontinuerliga)

Jag köper tex verkligen att x³-4 är kontinuerlig då x³:an täcker in allt och -4 innebär bara en förskjutning. Men när 4x hänger på x och är knuten till x³ så blir jag lite osäker på hur man tänker där...

-4x är en kontinuerlig funktion och summan av två kontinuerliga funktioner är kontinuerlig. Tidigare inlägg i tråden visar att f —>-oändl när x—>- oändl och att f—> oändl när x—>oändl. Den antar därför varje värde däremellan dvs att den är surjektiv. Däremot är f inte injektiv.

Tomten skrev:

-4x är en kontinuerlig funktion och summan av två kontinuerliga funktioner är kontinuerlig. Tidigare inlägg i tråden visar att f —>-oändl när x—>- oändl och att f—> oändl när x—>oändl. Den antar därför varje värde däremellan dvs att den är surjektiv. Däremot är f inte injektiv.

I see! Tack för svaret, bra att veta att man kan dela upp dom på det sättet!