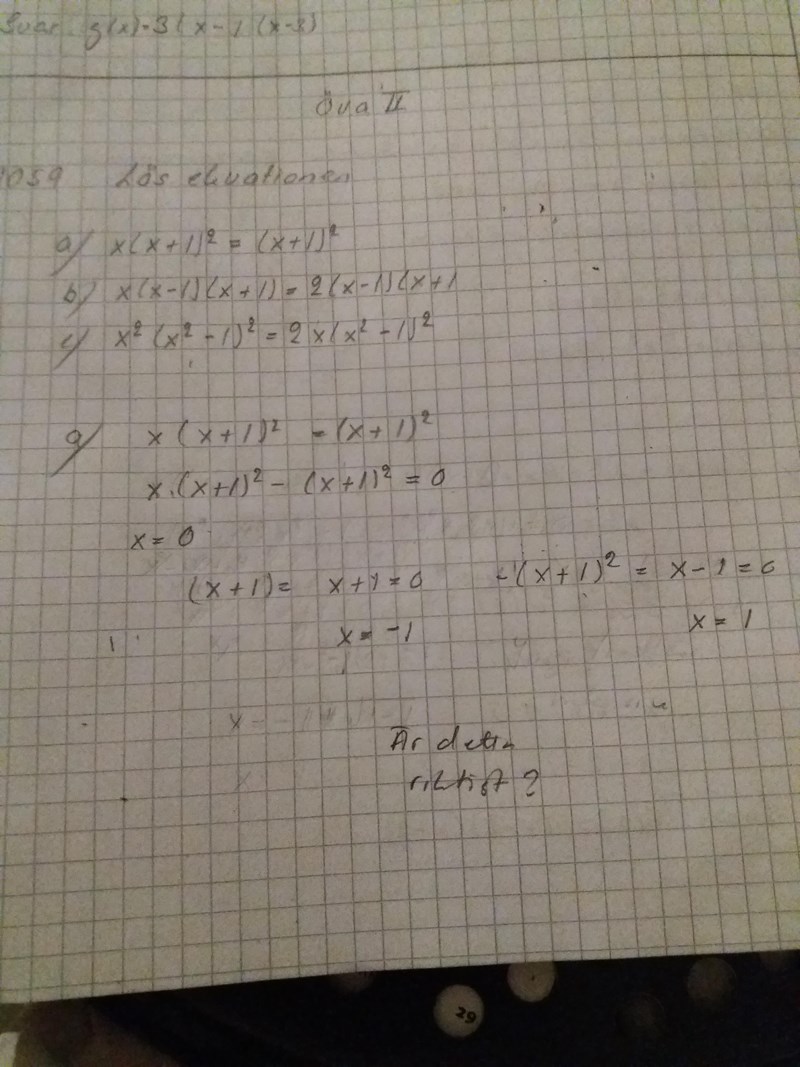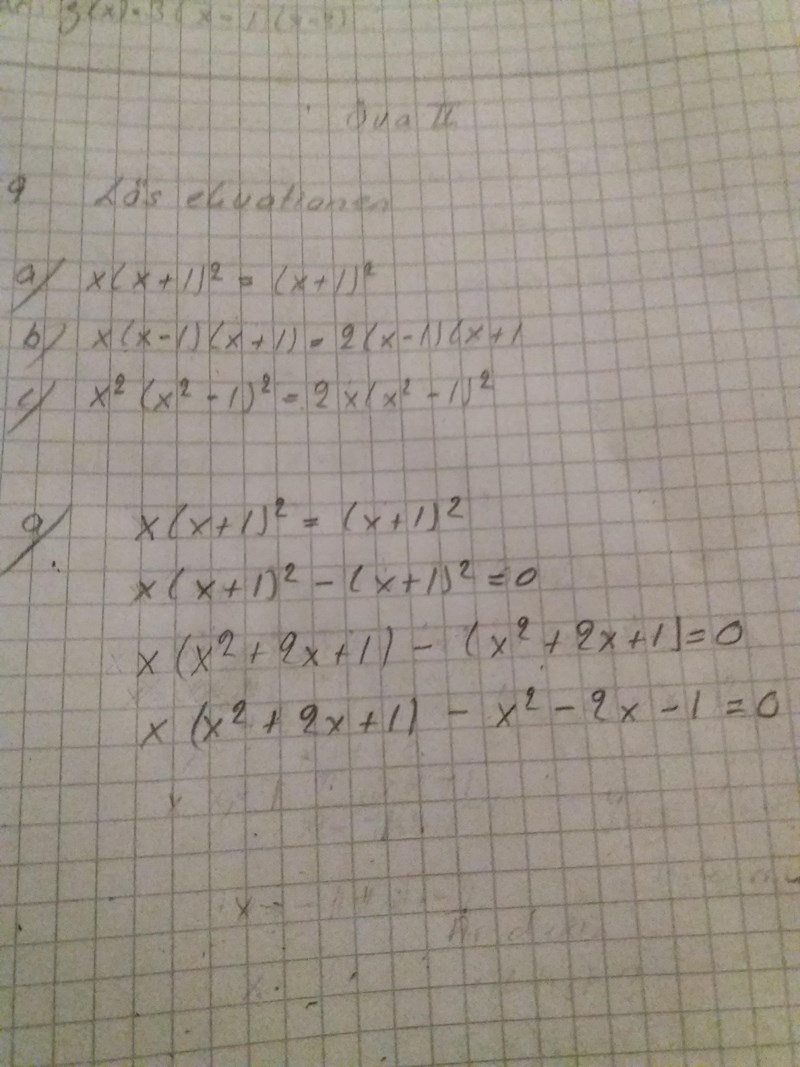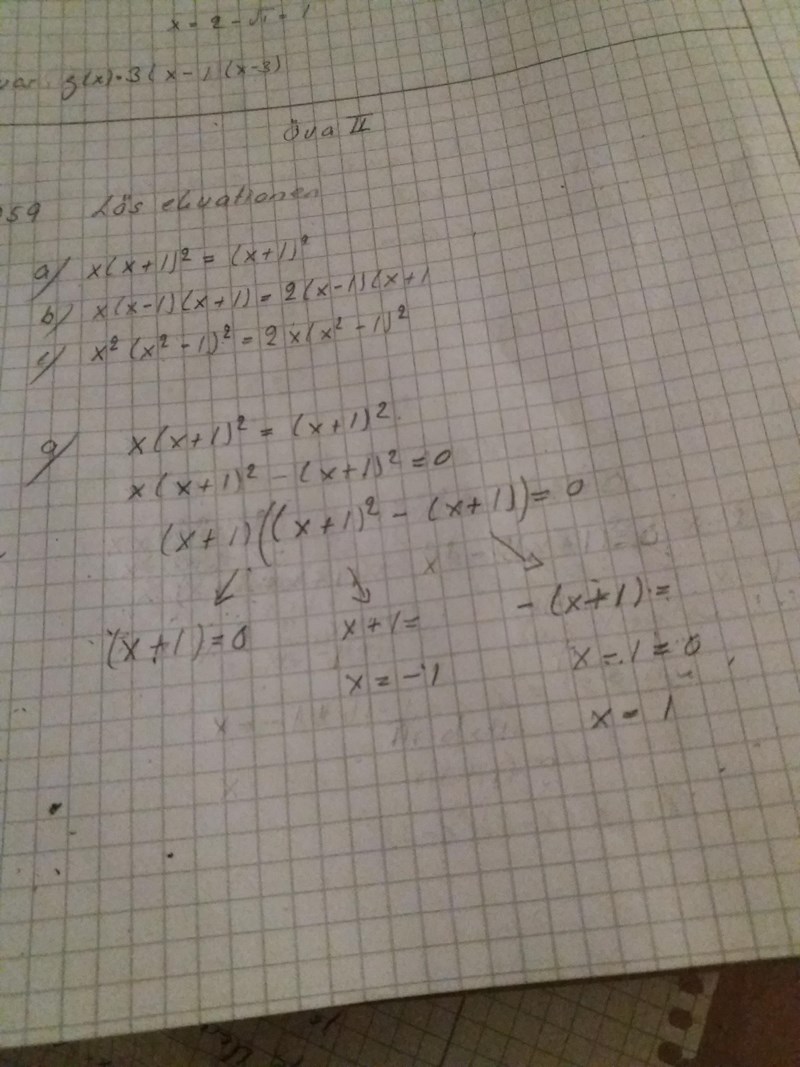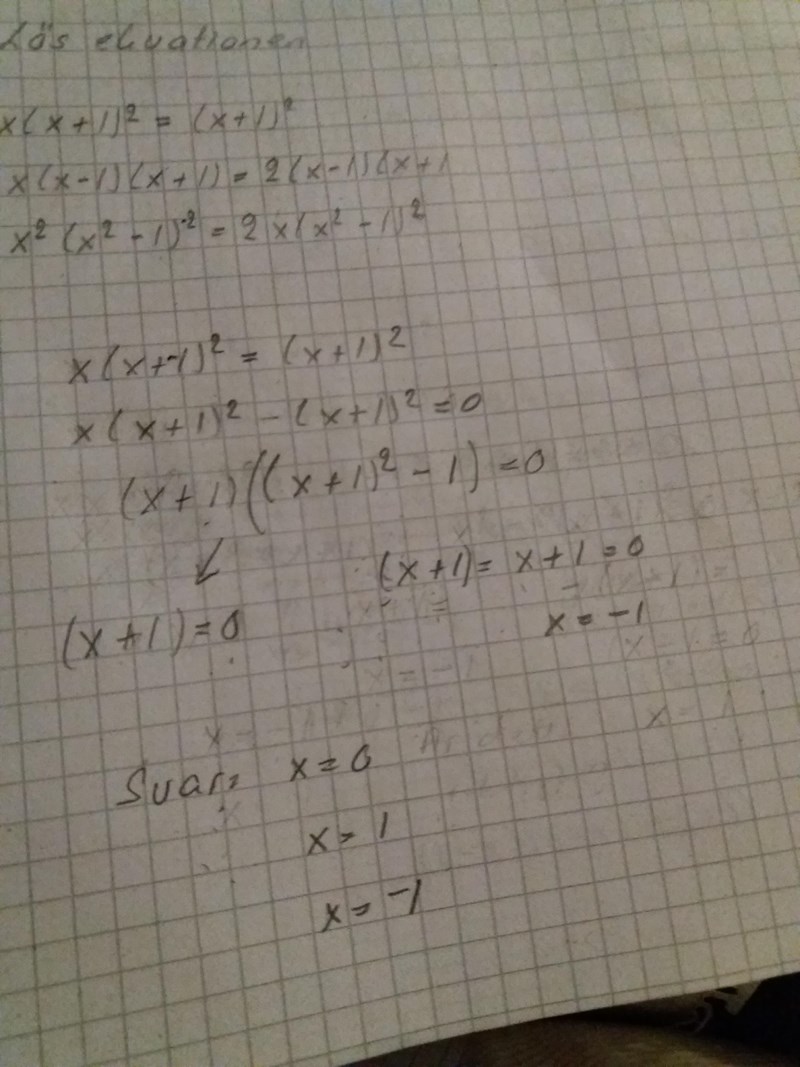Hur ska jag göra

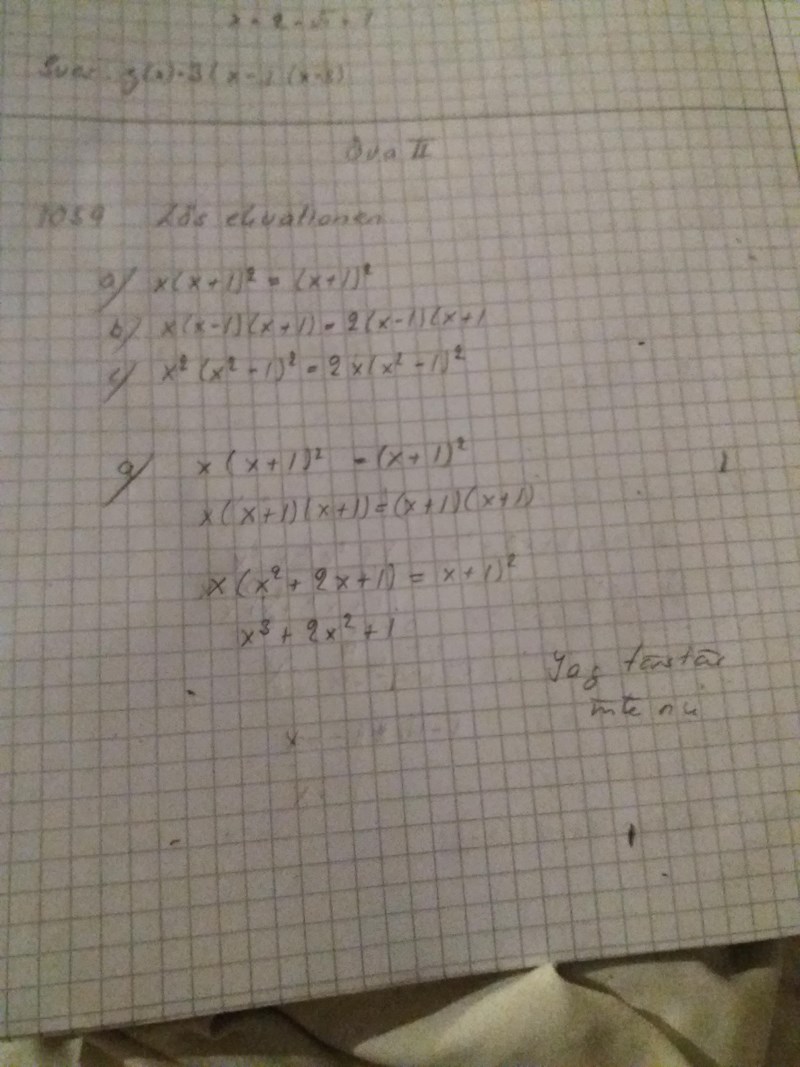
A)
x(1+1)^2=(x+1)^2
x(x+1)^2-(x+1)^2=0
(x-1)(x+1)^2=0
nollproduktregeln ger två svar
x=1 och x=-1
Päivi skrev :
Du ser direkt att om så är ekvationen uppfylld. Det ger dig en lösning.
Om däremot så kan du dividera bort den faktorn och får då en enkel ekvation för att hitta övriga lösningar.
Skriv om ekvationerna så att du har 0 i HL.
Faktorisera.
Använd nollproduktsmetoden.
EDIT - dubbelpost
Nu förstår jag inte vad ska jag dividera med?
Mera ledtråd
Päivi skrev :
Det går inte att följa dina tankegångar när du skriver så sporadiska anteckningar Päivi.
Du måste förklara hur du tänker och varför du skriver som du gör.
Det går inte göra så här heller.
Päivi skrev :Det går inte göra så här heller.
Hej Päivi.
OK, du vill fortsätta att följa vägen som Joculator och Dr. G pekade ut. Det går alldeles utmärkt.
Efter första steget, när du har samlat alla termer på vänster sida, har du två termer som båda innehåller en gemensam faktor. Du kan bryta ut den faktorn och på så sätt få en produkt av två faktorer i vänsterledet. Jag har gulmarkerat de två faktorerna i denna bild:

Om du tycker att det är krångligt med komplicerade faktorer så tycker jag absolut att du ska våga pröva att ersätta (substituera) det gulmarkerade med en symbol ett litet tag.
Kalla till exempel för .
Ekvationen kan då skrivas . Nu ser du att du kan bryta ut A ur vänsterledet.
Gör det och byt sedan tillbaka A till .
Du har inte kontrollerat din faktorisering (rödmarkerad i bilden) genom att följa rådet jag gav dig i denna kommentar Päivi. Gör det.
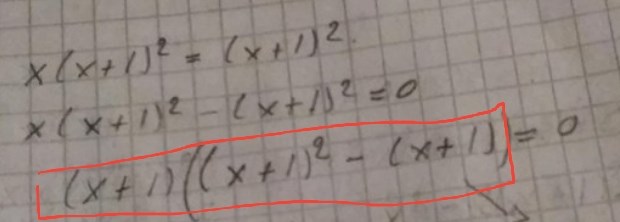
När du har gjort det tycker jag att du ska följa rådet du fick i denna kommentar och ersätta med A innan du faktoriserar.
Har just vaknat upp
Det ska stå ett istället.
Har du kontrollerat din faktorisering genom att följa mitt råd?
Det här var krångligare än jag anade alltså.
Varför svarar du inte på min fråga?
Varför följer du inte mina råd?
Jo, jag har tittat på det, Yngve!
Det var krångligare än så. Det finns x utanför parentesen också.
Päivi skrev :Jo, jag har tittat på det, Yngve!
Visa då det!
- Visa hur du ersätter med A innan du faktoriserar.
- Visa hur du kontrollerar om din faktorisering är korrekt.
Det här var värre än vad jag är van vid. Jag kan vänta med det här också till den 16/1
Päivi skrev :Det här var värre än vad jag är van vid. Jag kan vänta med det här också till den 16/1
Om du tycker att faktorisering är besvärligt så kan vi vänta med det Päivi.
Vi kan börja om från början på denna uppgift och istället välja den väg som jag föreslog i mitt första svar.
--------------------------------------------------
Töm hjärnan nu så börjar vi om från början.
Ekvationen lyder
Vi ser att uttrycket finns som faktor i både vänsterledet och i högerledet.
Om denna faktor är lika med 0 så lyder ekvationen och ekvationen är därmed uppfylld. Är du med på det?
Att den faktorn är lika med 0 innebär att , vilket är samma sak som att , vilket är samma sak som att . Är du med på det?
Så en lösning till ekvationen är alltså .
Om vi nu antar att så kommer faktorn att vara skild från 0. Är du med på det?
Det betyder att det är OK att dividera med den faktorn, så då gör vi det:
Nu kan vi förkorta med på båda sidor och vi får då endast följande kvar:
, Är du med på det?
Så en annan lösning till ekvationen är alltså .
Denna ekvation har alltså två lösningar, nämligen och .
För säkerhets skull kontrollerar vi våra lösningar:
ger följande vänsterled:
ger följande högerled:
Vänsterledet = Högerledet, alltså är lösningen OK.
ger följande vänsterled:
ger följande högerled:
Vänsterledet = Högerledet, alltså är lösningen OK.
--------------------------------------
Hängde du med på detta Päivi?
On du vill kan du sedan göra på samma sätt även på b- och c-uppgiften.
Vänta lite Yngve! Jag ska öppna den här sidan med den andra telefonen
Första är jag med på, ja
Nr. 2 är jag med på, ja
nr3 vänta. Är jag inte med på det.
Att något är skilt från noll, är jag inte med på än.
Jag
Päivi skrev :Första är jag med på, ja
Nr. 2 är jag med på, ja
nr3 vänta. Är jag inte med på
Vilken är nummer 3 för dig? Och vad i det är det du inte är med på?
När du frågar är du med på det?
Då räknar jag neråt på det viset. Första fråga är nr 1. Nu förstår jag dig fram till fråga 3.
Jag läser vidare och berättar vad jag förstår och inte förstår. Svarar på det här sättet att jag redigerar.
Päivi skrev :När du frågar är du med på det?
Då räknar jag neråt på det viset. Första fråga är nr 1.
OK så det du inte är med på är alltså följande:
Om vi nu antar att så kommer faktorn att vara skild från 0.
Vad är det du inte förstår med det?
Jag förstår att det blir -1. Att den ska vara skilt från noll.
Jag har börjat förstå, när du skrev till mig, där man kan läsa, om du förstår vad jag menar. Säger inte namnet på området.
Vi fick fram att x var -1 och nu skulle det vara skilt från noll.
Nu ligger jag här redan.
För säkerhets skull kontrollerar vi våra lösningar:
x=−1x1 ger följande vänsterled: (−1)(−1+1)2=(−1)(02)=0
x=−1x1 ger följande högerled: (−1+1)2=(−1)(02)=0
Vänsterledet = Högerledet, alltså är lösningen (x=−1)x1 OK.
Päivi skrev :Vi fick fram att x var -1 och nu skulle det vara skilt från noll.
Nej, x kan vara vad som helst.
För vissa värden på x så är ekvationen uppfylld och det är dessa värden vi letar efter.
Vi har sett att om x = -1 så är ekvationen uppfylld.
Då kan vi gå vidare och leta efter andra värden på x som också uppfyller ekvationen. Om det finns sådana andra värden på x som även de uppfyller ekvationen så är de inte lika med -1. Därför kan vi fortsättningsvis säga att vi letar vidare endast bland alla de x-värden som är skilda från -1.
--------
Med andra ord:
I det fall där x = -1 så har vi hittat en lösning.
I de andra fallen, dvs där x är skilt från -1 så fortsätter vi att leta efter lösningar.
-----------
Och det var inte x som var skilt från 0 om x är skilt från -1 utan det var faktorn som i så fall är skild från 0.
Det här var nytt sätt som jag inte var van vid. Det här är jätte bra att jag får se lite annat också än jag är van med, Yngve!
Jag skriver till Dig läs
Bra Päivi, nu har du räknat rätt och kommit fram till rätt svar.
------------
Men tyvärr är det är svårt att följa dina tankegångar och hur de leder fram till svaret.
Det framgår inte vad du gör eller varför. Det står inte varför du helt plötsligt dividerar med eller varför det är OK att göra det.
Jag vet att du siktar på de högre betygen. Om du ska kunna nå dem bör du träna på att presentera dina resonemang så att de går att följa.
Jag tycker att du noga ska läsa våra förslag till lösningar och då speciellt lägga märke till det resonemang vi för. Sedan tycker jag att du ska försöka härma oss genom att fortsättningsvis ha med förklarande resonemang i dina egna lösningar.
Jag borde alltså bli en papegoja. Det dröjer nog inte länge, innan jag är en goja. Jag har en hemma redan. Min härmar som bara den mig och hittar på egna meningar också. Jag försökte sätta mycket till dator, men misslyckades. Titta på c uppgift, Yngve
Päivi skrev :Jag borde alltså bli en papegoja. Det dröjer nog inte länge, innan jag är en goja. Jag har en hemma redan. Min härmar som bara den mig och hittar på egna meningar också. Jag försökte sätta mycket till dator, men misslyckades. Titta på c uppgift, Yngve
Haha. Jag menar nog inte riktigt att härma ord för ord utan istället att härma vårt sätt att presentera och förklara lösningarna.