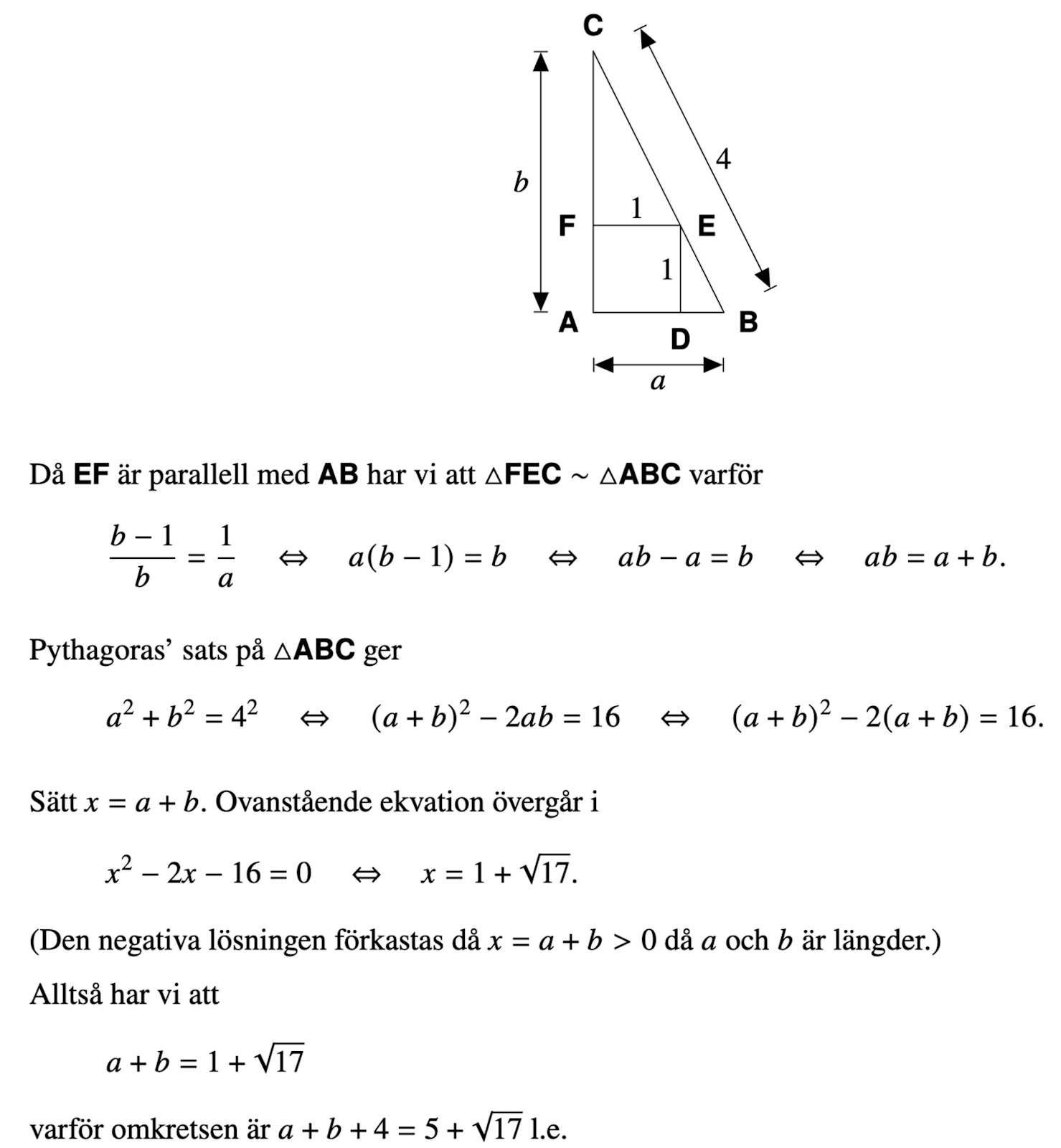
Hur skulle likformighet kunna användas ?
Är det rimligt att kalla ett av triangelns sidor för x-1 innan tillämpning av likformighet ?
Arup skrev:Är det rimligt att kalla ett av triangelns sidor för x-1 innan tillämpning av likformighet ?
Viken triangel är det du pratar om? Jag skulle kalla de okända sidorna i den stora trianglen för a och b.
jag skulle föredra x och y
Jag tönkte på att Pythagoras sats brukar skrivas a2+b2 =c2
Smaragdalena skrev:Jag tönkte på att Pythagoras sats brukar skrivas a2+b2 =c2
ok du har nog rätt. Jag tänkte mer på likformighet
Man behöver både Pythagoras och likformighet. Man kan kalla sina variabler vad man vill (och det var det jag gjorde, och du också).
Kommer du vidare på uppgiften?
varför skall man använda Pythagoras lilla stats, räcker det inte enbart med likformighet
Arup skrev:varför skall man använda Pythagoras lilla stats, räcker det inte enbart med likformighet
Hur då?
typ att ställa upp ett förhållande mellan de okända sidorna
Skall det bli 5+sqrt(17)?
japp
Den är lite lurig. Står det någon bra ledtråd i facit?
Om inte: Låt vertikal katet = b och horisontell = a
Topptriangeln är likformig med den stora och du kan få ett förhållande mellan a och b.
Anv. sedan detta förhållande i Pythagoras' sats som leder fram till en andragradsekvation.
Lös denna och du har (nästan) svaret. Addera 4 och du har svaret.
Uppgiften tillhör ej den vanliga typen utan är lite knepigare då a och b ej skall beräknas var för sig.
Nej. Det stod enbart att bara leta efter likformiga trianglar
Det är det lätta. Om jag nu inte har missat någon trivialt enkel lösning
Det stod enbart att bara leta efter likformiga trianglar
Går även smidigt utan likformighet.
Dra diagonal i kvadraten från nedre vänstra hörnet. Den delar stora triangeln i två delar.
Stora triangelns area kan skrivas på två sätt: .
a + b = ab (fast samma får man lika enkelt med likformighet)
a2 + b2 = 16 (Pythagoras)
a2 + b2 + 2ab = 16 + 2(a + b) (andra ekv + 2 gånger första)
(a + b)2 = 16 + 2(a + b) (a+b --> t)
t2 = 16 + 2t
t =
Omkretsen t + 4 = 5 +
snygg lösning ska kika på denna med ett kladdpapper
Det är nog samma eller liknande som Trinity2 skrev om i #12.
Det där med att gå på areor var egentligen ingen fördel,
visar bara hur man ofta kan göra på lite olika sätt.
Louis om man antar att en av länderna =a
är det fel att anta att kvadratens sida är a-1 eller ?
På så sätt skulle man kunna ställa upp ett förhållande
Kvadratens sida är 1. Sidan i en mindre triangel är a-1.
Du kan då ställa upp en likformighetsekvation som ger att a+b=ab.
Louis skrev:Det är nog samma eller liknande som Trinity2 skrev om i #12.
Det där med att gå på areor var egentligen ingen fördel,
visar bara hur man ofta kan göra på lite olika sätt.
Japp, din lösning (snygg) var så jag tänkte.
Jag skrev den själv så här: