Hur snabb måste rymdraketen vara om astronauten ska hinna fram på 10 år?

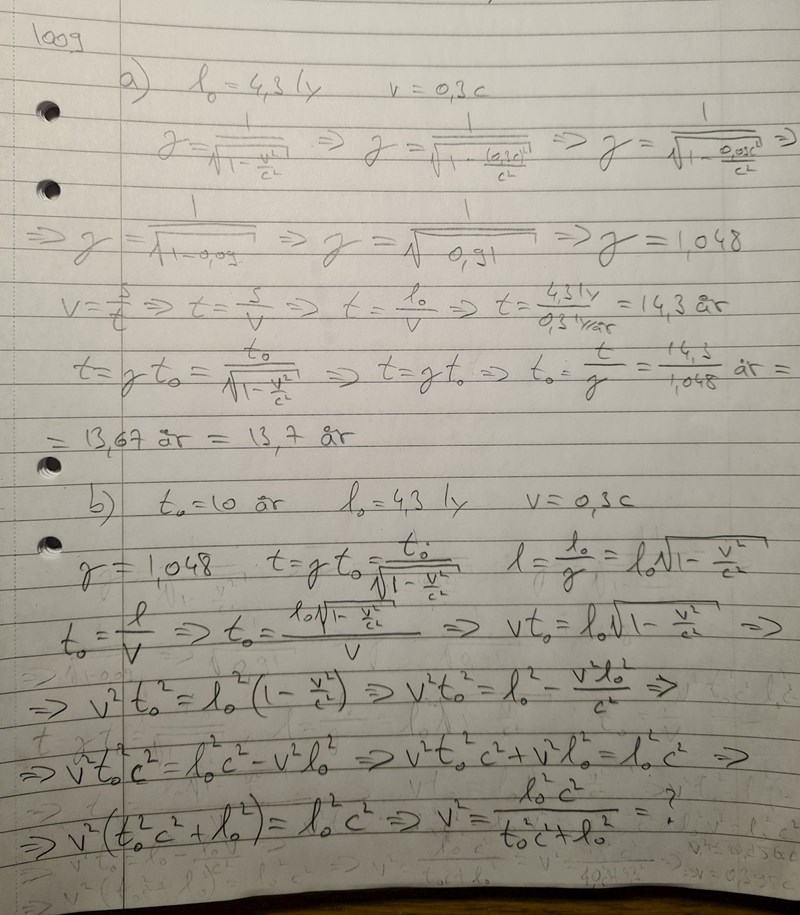
Du har iaf slagit fel på räknaren. Om man håller tungan rätt i munnen bör man få $v\approx0.395c$ med din formel. Testa att slå igen får du se :)

Tack för svaret, problemet är att jag har ett extra c^2 i nämnaren som du ser, vilket gör det svårt att uttrycka svaret i procent av c. Hur kom du fram att till att svaret ska vara 0,395c med ett extra c^2? 

Om du vill kan du slå in ditt uttryck precis som det står och får då $v^2\approx1.404\cdot 10^{16}\mathrm{m^2/s^2}$

$l_0\approx 4.068\cdot 10^{16}\mathrm{m}$

$t_0\approx 3.1536\cdot 10^8\mathrm{s}$

$c\approx 3\cdot 10^8 \mathrm{m/s}$

Jag tänkte också visa dig två sätt att förenkla räkningarna. Ett trick är att inse att det du kallar $l_0$ innehåller ljusets hastighet. Om $T_y$ är antalet sekunder på ett år är

$l_0=4.3\cdot T_y\cdot c$

Ditt uttryck för $v^2$ blir då

$v^2=\frac{4.3^2\cdot T_y^2c^2c^2}{t_0^2c^2+4.3^2\cdot T_y^2c^2}=\frac{4.3^2\cdot T_y^2c^2}{t_0^2+4.3^2\cdot T_y^2}$

Delar vi båda sidor med $c^2$ och drar roten ur får vi

$v=\frac{4.3\cdot T_y}{\sqrt{t_0^2+4.3^2 \cdot T_y^2}}\approx 0.395$

För att göra räkningarna riktigt enkla kan man räkna sträckan i  ljusår, tiden i år samt sätta ljushastigheten till 1, dvs $c=1$. Det förenklar uttrycket för $\gamma$ och tar bort alla tråkiga $c^2$ överallt.

Givet problemet får vi ekvationen (boosta astronauten $v$)

$\displaystyle l=tv\gamma$

med $\gamma=\frac{1}{\sqrt{1-v^2}}$ har ekvationen den positiva roten

$\displaystyle v=\frac{l}{\sqrt{l^2+t^2}}=\frac{4.3}{\sqrt{4.3^2+10^2}}\approx 0.395$

Edit: Fixade $t_0$

Tillägg: 21 nov 2022 23:27

Det ska självklart vara ett $c$ på slutet, dvs $v=0.395c$ för alla $v$ utom när vi använder $c=1$.

Tack för förklaringen, och ursäkta sent svar. Räknade med SI-enheterna meter och sekund och fick till sist rätt svar gällande ditt första exempel. Skulle du bara kunna förklara hur du kom fram till att l° kan uttryckas som 4,3•Ty•c? Kan man tolka det som att om 1 ljusår kan uttryckas Ty•c, så kan kan 4,3 ljusår uttryckas som 4,3•Ty•c?

Och kan l° respektive l i allmänheten uttryckas som du nämnt ovan? Knappar man in antalet sekunder för ett år för Ty och ljushastihhetens fulla värde för c, eller är värdet för c 1 i ditt andra exempel, eftersom c^2 försvann när du drog roten ur c^2 i täljaren? 

Partykoalan skrev:

 Kan man tolka det som att om 1 ljusår kan uttryckas Ty•c, så kan kan 4,3 ljusår uttryckas som 4,3•Ty•c?

Ja, exakt så.  Om man knappar in hela uttrycket för $l_0$ blir det:

$l_0=4.3\cdot T_y\cdot c=4.3\cdot (3.15\cdot 10^7\mathrm{s})\cdot (3\cdot 10^8\mathrm{m/s})$

Tanken är att du ska hitta ett $c$ i $l_0$ som du kan förkorta bort. Eftersom $t_0=10 T_y$ kan du förenkla det slutliga uttrycket ännu mer om du vill!

Det ska självklart vara ett $c$ på slutet, dvs $v=0.395c$ för alla $v$ utom när vi använder $c=1$. Först i mitt sista exempel visar jag hur man kan sätta $c=1$ och få väldigt enkla räkningar.

Som du märker är det ofta väldigt stora tal med massa kvadreringar i omlopp. Därför kan man tjäna på att använda andra enheter än SI. Men det får inte bli så att enheterna blir svårare att förstå än själva fysiken :)

Ja, precis. Jag börjar greppa det nu. Däremot får jag fel svar när jag knappar in de enheterna som du angav. Om t° är 10 år, c är 3,0×10^8 m/s Ty är antalet sekunder per år så borde svaret vara 0,395 eller hur?

En sak till, borde 4,3 ljusår anges som sträckan i meter, dvs 4,3× 9,461×10^15 m eller bara uttryckas som 4,3 ly? Det har blivit en röra och jag har försökt knappa in rätt värden flera gånger nu så att svaret ska bli rätt. Och där jag har markerat med pilen borde ett c stå i täljaren, som du sa eller hur? Efter rottecknet så finns bara ett c kvar där? 

Det du vill göra är att få ett förhållande mellan $v$ och $c$ alltså ett uttryck för $\frac{v}{c}$

Vi har uttrycket

$\displaystyle v^2=\frac{4.3^2T_y^2c^2}{t_0^2+4.3^2T_y^2}$

Delar vi båda sidor med $c^2$ får vi

$\displaystyle \frac{v^2}{c^2}=\frac{4.3^2T_y^2}{t^2_0+4.3^2T_y^2}$

Drar vi roten ur båda sidor får vi

$\displaystyle \frac{v}{c}=\frac{4.3T_y}{\sqrt{t^2_0+4.3^2T_y^2}}$

Slår vi in det på räknaren med $T_y\approx 3.15\cdot 10^7$ samt $t_0\approx 3.15\cdot10^8$ får vi

$\displaystyle \frac{v}{c}\approx 0.395$

Detta är samma sak som att säga $v\approx 0.395c$ eller 39.5% av ljushastigheten.

Okej, jag förstår. En sak till, vad är skillnaden mellan den digitala lösningen som exkluderar Ty och ditt förslag som inkluderar Ty? 

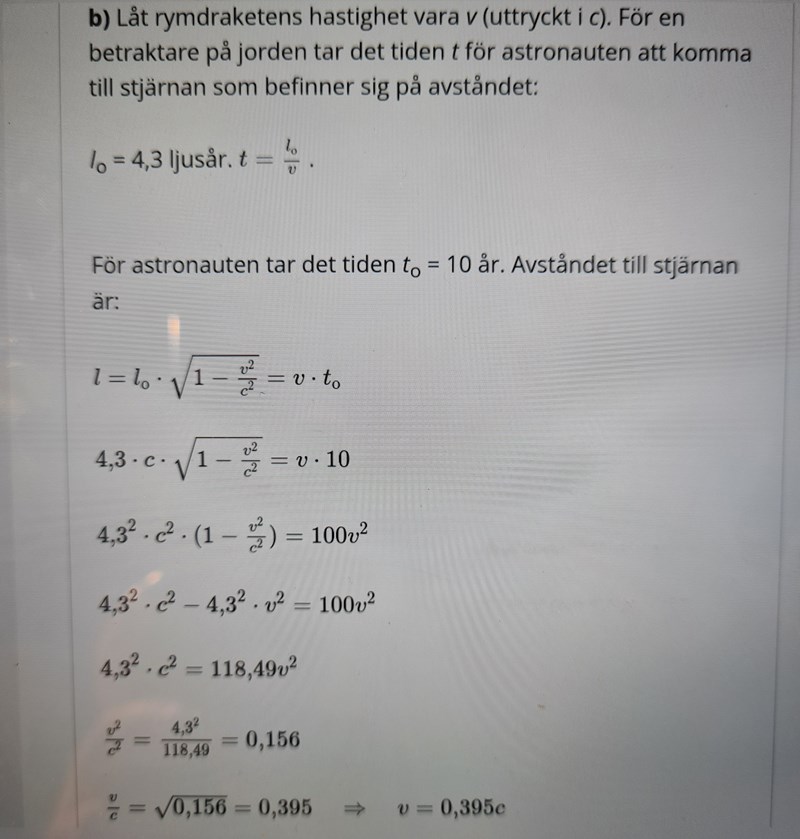
Istället för SI-enheter och sekunder har de räknat med tidsenheten år. Det innebär att $T_y=1$

Tack för hjälpen!