Hur snabbt växer kubens volym vid den tidpunkt volymen är 27 cm^3?

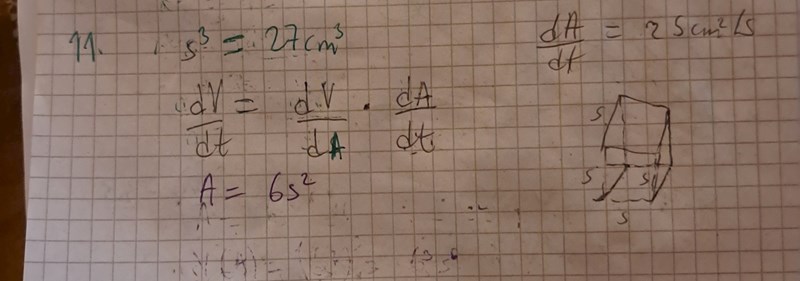
Du kan skriva om volymfunktionen V(s) till en funktion som är beroende av arean A. Begränsningsarean av en kub är $A=6s^2$. Om vi löser ut s därifrån, får vi:

$$\begin{gathered} A=6s^2 \\ s={\left(\frac{A}{6}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} \end{gathered}$$

Detta A kan du sedan sätta in i volymformeln för kuben, och sedan derivera med avseende på A. :)

Smutstvätt skrev:

Du kan skriva om volymfunktionen V(s) till en funktion som är beroende av arean A. Begränsningsarean av en kub är $A=6s^2$. Om vi löser ut s därifrån, får vi:

$$\begin{gathered} A=6s^2 \\ s={\left(\frac{A}{6}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} \end{gathered}$$

Detta A kan du sedan sätta in i volymformeln för kuben, och sedan derivera med avseende på A. :)

Då får jag dV/dA=A/2.

V(s)=s^3. dV/ds=3s^2=3*A/6=A/2.  Hur man skriver V(s) till V(A) vet jag ej. 

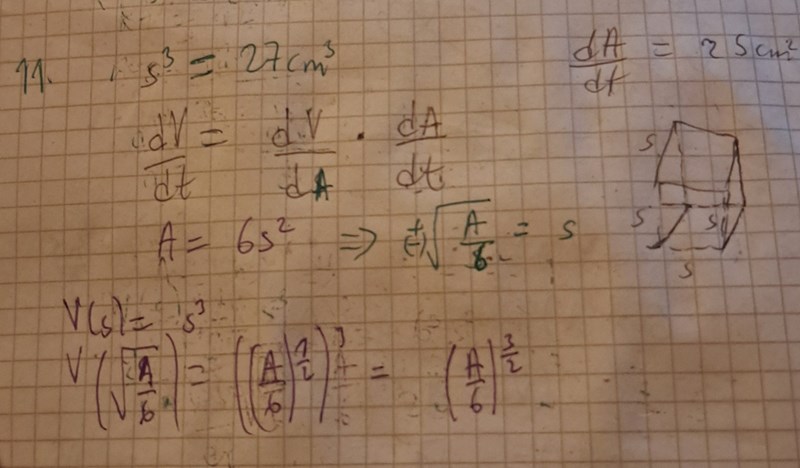
Är det inte precis det du har gjort på sista raden?

Laguna skrev:

Är det inte precis det du har gjort på sista raden?

Aa jo det måste vara rimligt. Men om vi deriverar detta så har vi ingen aning vad A är ? dV/dA=3/2*sqrt(A/6). Jag vet ej om det är tänkt att lösa ut s ur s^3=27 cm^3 för då får vi s=3. då vet vi att A(3)=6*3^2=54 cm^2. Jag får dock 

dV/dt= 3/2*3*25=225/2. Facit håller ej med 

När du deriverar (A/6)^3/2 så har du en inre derivata också: 1/6.

Laguna skrev:

När du deriverar (A/6)^3/2 så har du en inre derivata också: 1/6.

Juste det glömde jag.