Hur stor andel av figuren är färgad?

Det var bra start, men det blev fel när två bråk adderades.

(Försök 1) Hur fick du en 3:a här?

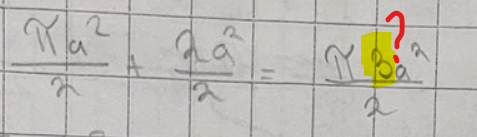
Det stämmer ju inte att $\pi + 2 = 3\pi$ eftersom $\pi + 2 \approx 3,14 + 2 = 5,14$ medan $3\pi \approx 3 \cdot 3,14 = 9,42$.

Därmed stämmer det inte att $\pi\,a^2 + 2\,a^2 = 3\pi\,a^2$.

Däremot kan man bryta ut $a^2$, vilket ger $\pi\,a^2 + 2\,a^2 = (\pi + 2)\,a^2$

(Försök 2) Hur fick du en 2:a här?

Det stämmer ju inte att $\underbrace{\pi + 1}_{\approx 4,14} = \underbrace{2\pi}_{\approx 6,28}$, så det stämmer inte heller att $\pi\,a^2 + a^2 = 2\pi\,a^2$.

Notera dock att redan bråket $\dfrac{a^2}{8a^2}$ inte var korrekt. När $\dfrac14$ förlängs så att nämnaren blir $8a^2$, så förlänger man med $2a^2$. Bråket 1/4 efter förlängningen borde ha varit $\dfrac{2a^2}{8a^2}$.

Notera också att det vore enklare att förkorta $\dfrac{\pi\,a^2}{8\,a^2}=\dfrac{\pi}{8}$ och sedan förlänga $\dfrac14 = \dfrac28$

(Försök 3) Här blev förenklingen av det sammansatta bråket fel:

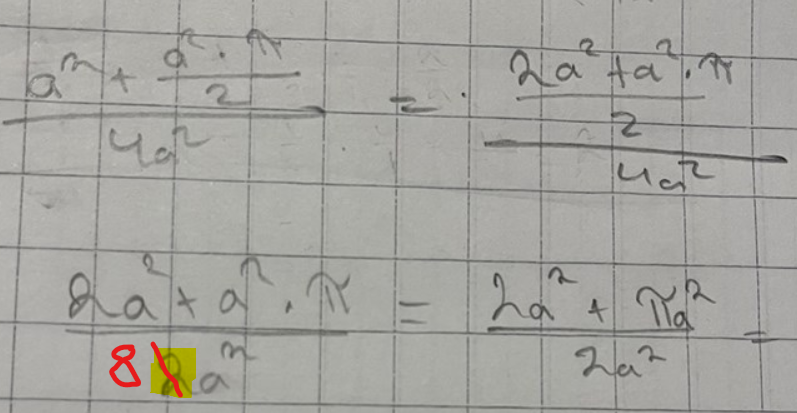
I nämnaren borde man ha fått $2 \cdot 4a^2 = 8a^2$.

Tack för ditt utförliga svar! Det var väldigt hjälpsamt. 
Jag gav det ett till försök:

Där svaret äntligen blev korrekt. Ser utlösningen okej ut?