Hur vet man om en funktion är sned eller horisontell
Hej! Jag förstår inte hur man vet om en funktion är en sned asymptot eller bara en noll horisontell asymptot.
jag trodde att när det blev noll kvar i en funktion när man gör lim x går mot oändligheten att det betydde direkt att funktionen är en sned asymptot och man måste göra liggande stolen. Men sen gjorde jag denna uppgiften
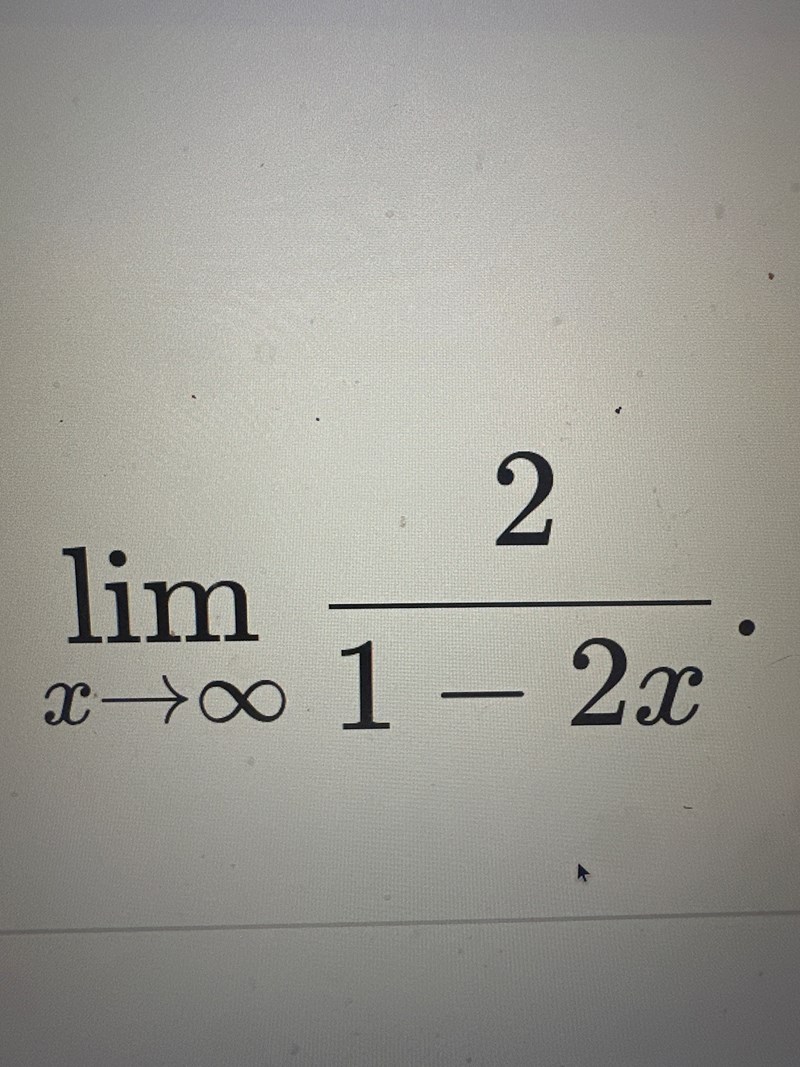
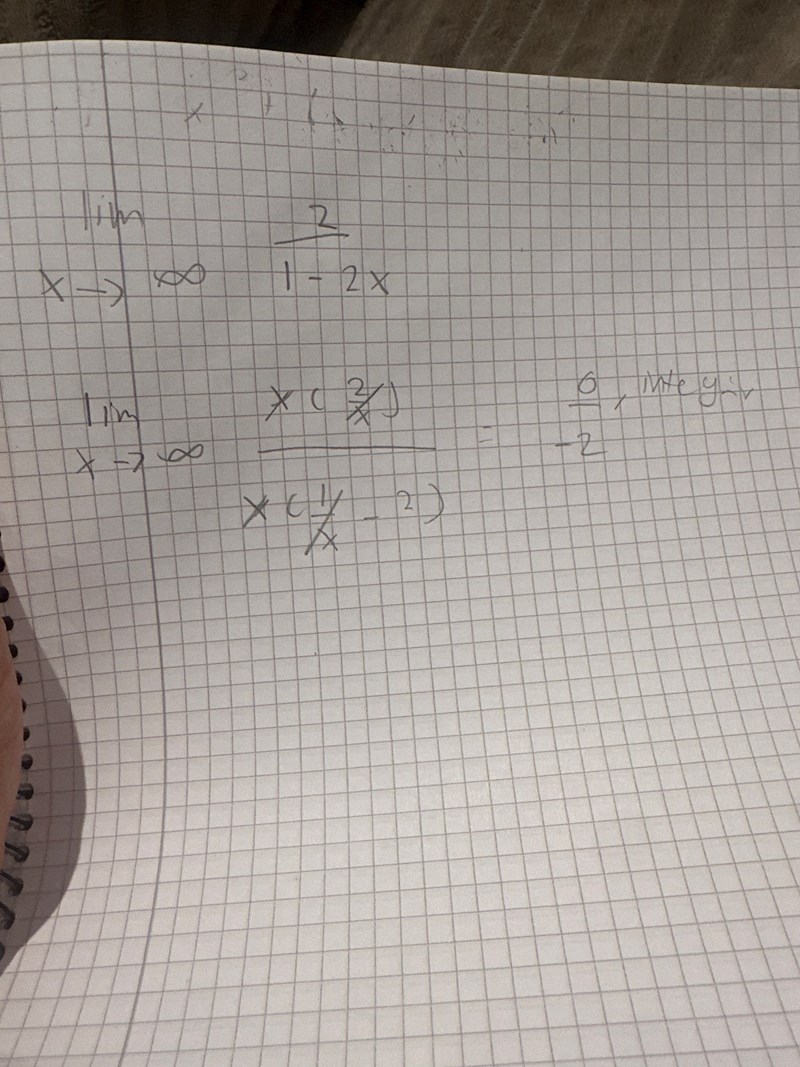
Jag kollade på facit och det stig att den är en horisontell asymptot som har värdet noll
så hur vet man genom att göra en lim x går mot x är funktionen är sned? Vad är det som indikerar det. Jag har försökt kolla på videos men hittade inget som gav svar på min fråga
"lim x går mot oändligheten att det betydde direkt att funktionen är en sned asymptot"
Det är sant. Om asymptoten inte är horisontell har den inget gränsvärde och lim = +oo eller -oo då x->+oo eller -oo.
Ditt gräsnvärde existerar och är 0, alltså är asymptoten horisontell.
Notera att lim=+oo (eller -oo) då x->a betyder att det finns en vertikal asymptot, x=a.
Detta är dock inte detsamma som lim=+oo eller -oo då x->+oo eller -oo.
Rita lite kurvor så ser du det klarare. T.ex.
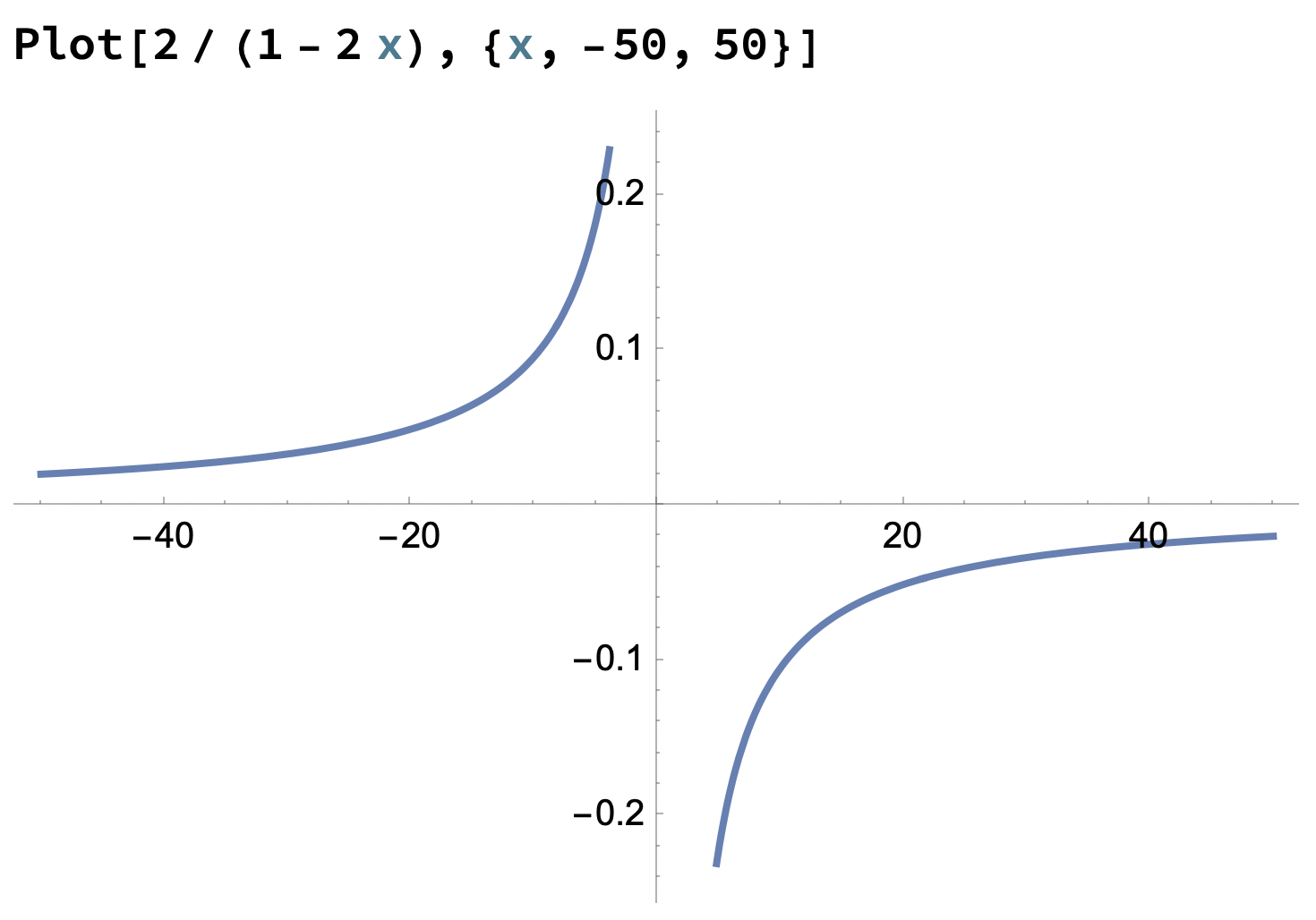
Det är alltså en funktions Asymptot som kan vara sned inte funktionen. Den aktuella funktionen hade alltså ingen sned asymptot. Om vi t ex ändrar den till f(x)= 2/(1-2x) + x, så kommer |f(x)-x| —>0 när x—> oändl och då blir linjen y=x en sned asymptot.
Så om man utför en lim x går mot oändlighet beräkning och det finns ett X kvar i täljare eller nämnare som inte kan förenklas bort så betyder det att funktionen har en sned asymptot ?
Tror jag förstår hur du menar, men du uttrycker det inte helt rätt. När x—> oändl så går alla x:en i uttrycket mot oändl. Då blir inga x ”kvar”.
En funktion f(x) har den sneda asymptoten y=kx+m om och endast om |f(x)-(kx+m)|—>0 när x—>oändl.
Jag menar typ så här
 Det är här jag hade lagt denna funktion i lim x går mot oändlighet
Det är här jag hade lagt denna funktion i lim x går mot oändlighet
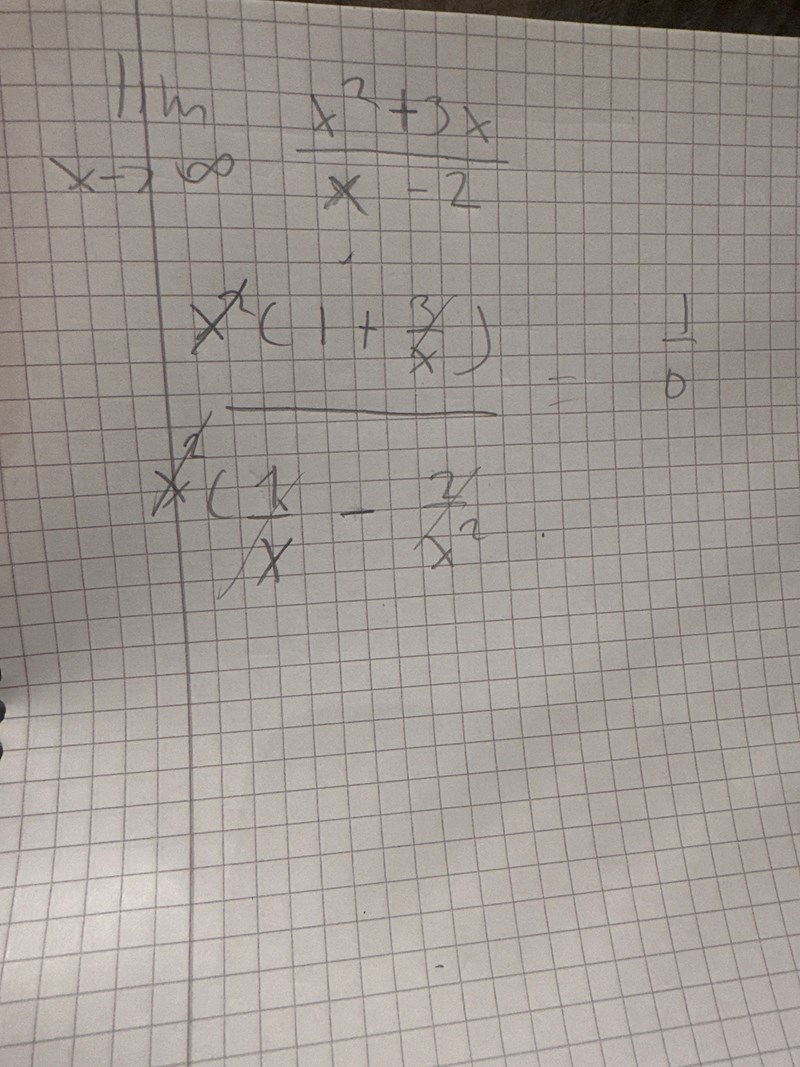
här blir det också noll om jag inte har gjort något fel. Hur vet jag om jag inte har fått information innan om vilken typ av asymptot funktionen är
den vertikala kollar jag i nämnaren på vad som gör att den inte blir definerad
medan om jag kollar om den är horisontell eller sned asymtot gör jag detta genom lim x går mot oändlighet- fast nu är jag förvirrad i hur jag ska veta när den är sned och när den är horisontell utan med hjälp av en grafritate
På det sättet gör du det svårare än det behöver vara. Om uppgiften bara ges som en funktion i form av ett bråk mellan två polynom, skulle jag råda dig att rita fknen till dig själv utan att ta med figuren i lösningen (såvida inte detta krävs). Om du ritar någorlunda korrekt, så ser du snart vart det barkar hän och då vet du vad du behöver visa. Om täljarens gradtal överstiger nämnarens med +1, så räkna med att leta efter sned asymptot. Om inte så är asymptoterna parallella med koordinataxlarna. Men även funktioner som INTE är polynom kan ha asymptoter, vågräta, lodräta eller sneda.
I din hantering ovan ser jag ett par fel när du bryter ut: x2+3x= x(x+3) och x-2=x(1-2/x), och kvoten däremellan går mot oändl när x går mot oändl, (det är x et framför +3 som går mot oändl.) så asymptoten syns inte. Håll fast vid regeln jag gav dig i mitt förra inlägg, så undviker du en onödig felkälla.
R.zz skrev:Jag menar typ så här
Det är här jag hade lagt denna funktion i lim x går mot oändlighet
här blir det också noll om jag inte har gjort något fel. Hur vet jag om jag inte har fått information innan om vilken typ av asymptot funktionen är
den vertikala kollar jag i nämnaren på vad som gör att den inte blir definerad
medan om jag kollar om den är horisontell eller sned asymtot gör jag detta genom lim x går mot oändlighet- fast nu är jag förvirrad i hur jag ska veta när den är sned och när den är horisontell utan med hjälp av en grafritate
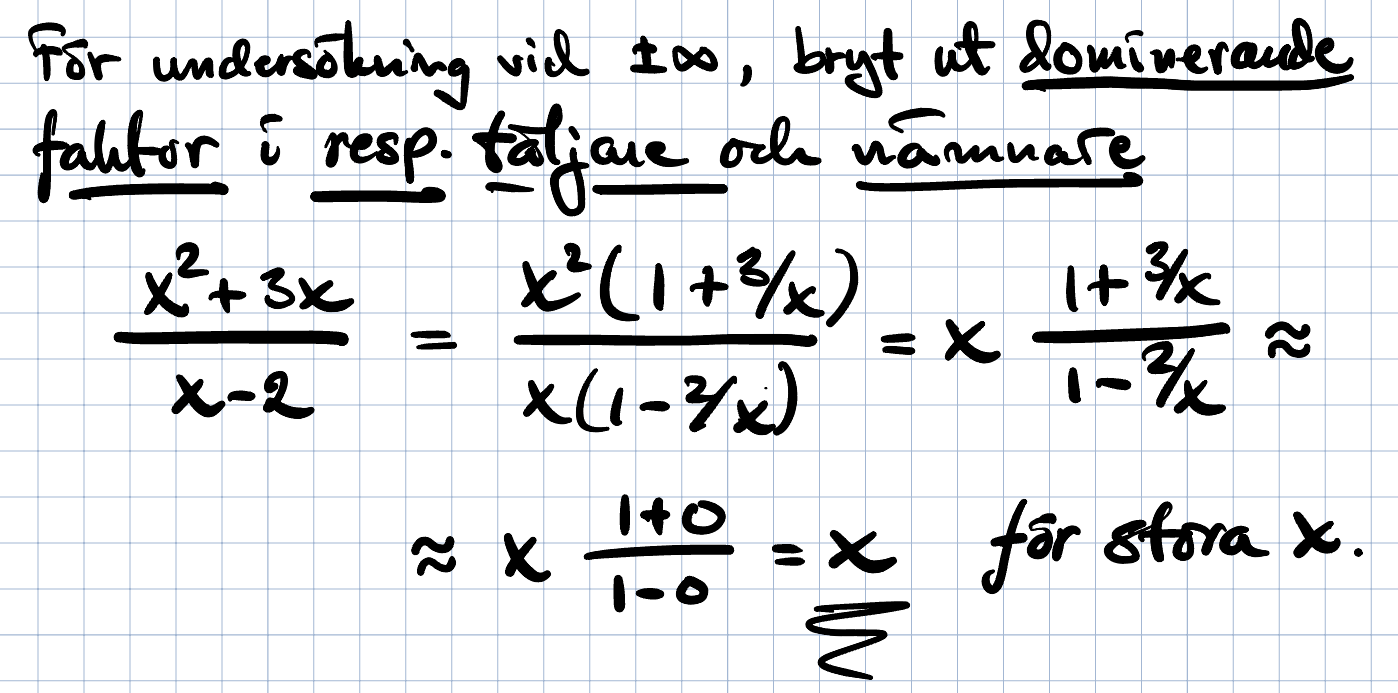
I det senaste exemplet är f(x) = (x2+3x)/(x-2) som kan skrivas x + 5 + 10/(x-2). Den sneda asymptoten är alltså x+5.
Tomten skrev:På det sättet gör du det svårare än det behöver vara. Om uppgiften bara ges som en funktion i form av ett bråk mellan två polynom, skulle jag råda dig att rita fknen till dig själv utan att ta med figuren i lösningen (såvida inte detta krävs). Om du ritar någorlunda korrekt, så ser du snart vart det barkar hän och då vet du vad du behöver visa. Om täljarens gradtal överstiger nämnarens med +1, så räkna med att leta efter sned asymptot. Om inte så är asymptoterna parallella med koordinataxlarna. Men även funktioner som INTE är polynom kan ha asymptoter, vågräta, lodräta eller sneda.
I din hantering ovan ser jag ett par fel när du bryter ut: x2+3x= x(x+3) och x-2=x(1-2/x), och kvoten däremellan går mot oändl när x går mot oändl, (det är x et framför +3 som går mot oändl.) så asymptoten syns inte. Håll fast vid regeln jag gav dig i mitt förra inlägg, så undviker du en onödig felkälla.
hur menar du att gradtalen ska överstiga nämnaren, hur hade detta fungerat?
de uppgifter vi har blivit tilldelade är då en funktion som man ska bestämma asymptotererna, och man bestämmer då de om den andra asymtoten är horisontell eller sned. Och man ska göra detta utan att behöva rita upp någon graf
fast jag förstår ännu inte hur jag kan se om när funktion läggs i x lim går mot oändlighet- hur man ser om den är horisontell eller sned. Min lärare sa att när funktionen inte går att göra lim går mot x så är den sned sen ska man utföra liggande stolen , fast när är det ”fel”, är det när x finns kvar i täljare eller nämnare ?
Om den är horisontell så är y= m konstant. Då har f(x) gränsvärdet m när x—>oändl.


