I det dunkla månskenet blinkar två fyrar. Bevisa hur de blinkar vid en viss tidpunkt.

Jag kan inte se att det du kommit fram till skulle vara ett circelresonemang.  $\frac{1}{\alpha }+\frac{1}{\beta }=1$ är givet i uppgiften. Det kan du alltså använda i ditt bevis.

(Intervallen är irrationella, annars borde man kunna visa att dom kommer att blinka precis vid ett minutskifte, och därmed även visa att dom kommer kunna blinka vid samma tidpunkt. Det skulle ha inneburit två blink den minuten.)

Inte? Hmm, det känns som en för lätt lösning, med tanke på att uppgiften ska vara "extra klurig", men det får väl duga för nu, åtminstone. Tack så mycket, och välkommen till Pluggakuten!

Jag tycker inte att det är ett giltigt bevis för mina ögon eftersom det utgår från andelar av intervall mellan blinkningar  och inte säger mig något om hela blinkningar. Det ger heller ingen ny förståelse av problemet vilket är vad jag generellt vill se i bevis såsom exempelvis förklara varför det inte kan ske någon blinkning under det första intervallet eller att fallet då två blinknigar sker infinitessimalt nära varandra alltid sker på olika sidor om ett heltal. 

Tag följande stegning med $\alpha = \sqrt{7}$ och $\beta = (7 + \sqrt{7})/6$ för illustration av fenomenet med tajta blinkningar vid 8

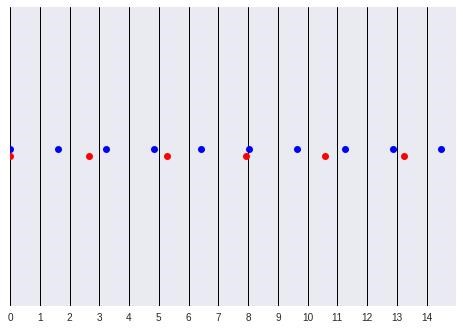
Jag överaskas dock av att jag själv verkligne inte kommer någon vart med något jag själv skulle tycka var ett tillfredställande bevis. 

Jag tycker ungefär samma sak; det känns som att jag bara vispar runt lite, kommer tillbaka på ruta ett, och sedan säger "titta, jag fick samma sak, beviset är klart!", men det är det enda jag kommer på, tyvärr. Om du kommer på något, skriv gärna en kommentar! Jag får fråga någon lärare i veckan. :) Tack för en fin bild och ett bra försök!

Jag håller med om att det inte är något bevis. Jag var skeptiskt till huruvida det var ett cirkelresonemang men där kanske jag har fel.

Det är en intressant uppgift. Det känns som att det borde gå att lösa med induktionsbevis.

Man kan visa att det gäller för grundfallet n=2. Frågan är hur man skulle gå tillväga med att visa att det gäller för n+1 givet att det gäller för n.

Izor skrev:

Jag håller med om att det inte är något bevis. Jag var skeptiskt till huruvida det var ett cirkelresonemang men där kanske jag har fel.

Det är en intressant uppgift. Det känns som att det borde gå att lösa med induktionsbevis.

Man kan visa att det gäller för grundfallet n=2. Frågan är hur man skulle gå tillväga med att visa att det gäller för n+1 givet att det gäller för n.

Hmm, vi ska gå igenom induktionsbevis nästa vecka, så jag tror inte att det är tanken men det är värt ett försök! Det får bli imorgon, dock. :)

https://jsfiddle.net/spaztj5e/38/

Jag gjorde en liten JS fiddle för att illustrera förhållandet mellan alpha och beta.

Det blir tydligt att påståendet stämmer, nu är det bara beviset som återstår :)

Hej!

Fyrarna Alfa och Beta är synkroniserade för första gången vid tidpunkten 0 och nästa synkronisering sker vid tidpunkten $t$. Vid tidpunkten $t$ blinkar Alfa för p:te gången och Beta för q:te gången, där $p$ och $q$ är relativt prima (om fyrarnas frekvenser är olika). Det gäller att $t = p\alpha$ och även att $t=q\beta$, vilket innebär att kvoten $\alpha/\beta$ är lika med det rationella talet $q/p$.

Kan man använda denna observation till något?

Hmm, nja inte riktigt. Det medför att jag kan skriva ekvationen $p\alpha+q\beta=2t$, alternativt $\frac{p\alpha}{q\beta}=\frac{t}{t}=1$, men det ger inte heller riktigt något. Kan man få en till ledtråd? :)

@Albiki. Det är möjlit att det där är någon smart ledning som leder oss in i något intressant men vill ändå påminna tråden om att vi har kriteriet i uppgiften att $\alpha$ och $\beta$ är irrationella så de kommer aldrig faktiskt att bli synkroniserade igen. Om så ska kunna ske måste $\alpha / \beta$ vara rationellt men utifrån kriteriet $1/\alpha + 1/\beta = 1$ så måste denna kvot istället vara irrationell eftersom

$1/\alpha + 1/\beta = 1$

$1 + \alpha/\beta = \alpha$

$\alpha/\beta = \alpha- 1$ och HL är irrationellt. 

Det kan förstås finnas någonting man kan göra med detta ändå med approximationsargument men det andra  synkroniseringstilllfället finns inte. 

Hej!

Fyren Alfa blinkar vid tidpunkterna $a_k = k\alpha$ och fyren Beta blinkar vid tidpunkterna $b_k = k\beta$, där $k \in \mathbb{N}$. Blink-frekvenserna $1/\alpha$ och $1/\beta$ är irrationella tal i intervallet $(0,1)$; det medför att under ett tidsintervall av längd $1$ kommer Alfa att blinka högst en gång och Beta att blinka högst en gång och att under ett sådant tidsintervall kommer det sammanlagda antalet blinkningar att vara 0, 1 eller 2. 

Anta att det finns ett heltal $n>1$ sådant att det sammanlagda antalet blinkningar under tidsintervallet $(n-1,n)$ är $0$ eller $2$. Om man kan visa att detta leder till en motsägelse så blir slutsatsen att det sammanlagda antalet blinkningar under varje heltals-intervall $(n-1,n)$ är exakt $1$.

Fall 0. Det sammanlagda antalet blinkningar under tidsintervallet $(n-1,n)$ är lika med noll. Det är bara möjligt om $1/\alpha$ och $1/\beta$ båda är nära noll. Men kravet $1/\alpha + 1/\beta =1$ gör att åtminstone en av termerna måste ligga nära $1$.

Fall 2. Det sammanlagda antalet blinkningar under tidsintervallet $(n-1,n)$ är lika med två. Det är bara möjligt om $1/\alpha$ och $1/\beta$ båda är nära $1$. Men kravet $1/\alpha + 1/\beta =1$ gör att åtminstone en av termerna måste ligga nära $0$.

Aha, då förstår jag! Tack så mycket! 

Jag känner också att beviset borde se ut som något liknande det du formulerat Albiki men jag är skeptisk då du inte använder faktumet att n är ett heltal någonstans. Du använder ju bara att intervallets bredd är 1 men det går ju att hitta andra intervall $(n + \epsilon, n + 1 + \epsilon)$ som har bredd 1 men som har 0 eller 2 blinkningar under perioden perioden så var används heltalsegenskapen?

Sedan är nära 0 lite  oklar för mig men jag antar att 'nära 0' avser att ligga i intervallet (0,1/2) och 'nära 1' att ligga i intervallet (1/2, 1).

Heltalsegenskapen göms i formuleringen "[...] Det medför att under ett tidsintervall av längd 1 kommer Alfa att blinka högst en gång "

Jag menar att intervallet börjar på ett heltal, inte att intervallets bredd är ett heltal. 

Tror att jag har ett alternativt bevis nu. Utgår från att representera talen på formen 

$\alpha = 1+a$

$\beta = 1 + 1/a$

där a är ett positivt tal mindre än 1 och är ganska enkellt och konstruktivt snarare än genom induktion eller mortsägelse. Ska dock sova på den så att formuleringen blir klarare än vad som lär flöda ur mina fingrar 0:00.

Vi följer SeriousCephalopods notation och inför

$\alpha= 1+a$

$\beta = 1 + 1/a$.

Påståendet är ekvivalent med att visa att det inte existerar heltal $m, n > 0$ så att

$\left \lfloor{m+m/a}\right \rfloor=\left \lfloor{n+na}\right \rfloor$

för irrationella $a$. Fixera $m,n$.

Fall 1: $a>m/n$. I detta fall är V.L. $<>$ (eftersom V.L. är en avtagande funktion) medan H.L. $\geq m+n$ (eftersom H.L. är en växande funktion).

Fall 2: $m/n>a>0$. I detta fall är V.L. $\geq m+n$ medan H.L. $<>$.

Notera att vi inte betraktar $a=m/n$ eftersom detta inte är ett irrationellt tal! Således finns det för godtyckliga $m,n$ inget irrationellt tal $a$ som uppfyller likheten.

Byrackans bevis är en betydligt koncisare och klarare version av det jag skisserade igårkväll så postar inte något eget utan ger bara tummen upp till den.