I en triangel är ena sidan = a. De övriga sidorna förhåller sig 2:3 . Vilken är max- arean?

Är triangeln rätvinklig alltså? Har du en bild av uppgiften?

Triangeln är Inte rätvinklig , har ingen bild.

Ett sätt som ger lösningen direkt är att utnyttja herons formel. Om vi ansätter att de andra två sidorna har längden $2x$ och $3x$ respektive ger formeln arean uttryckt som en funktion i $x$. Den kan vi sedan ta derivatan av och få fram maximipunkten. Däremot är detta inte särskilt rolig algebra!  (Det blir faktiskt rätt trevligt, jag hade fel!)

Det ger oss vår lösning av $3a^2/5$. Har inte kommit på något som använder ma4 formler, låt mig tänka lite.

Med ma4:

Om vi döper vinkeln mittemot sidan med längden $a$ till $\alpha$ har vi figuren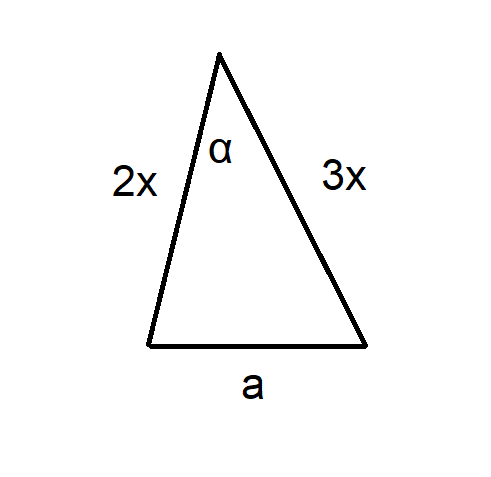

Areasatsen ger oss att arean, $A$ kan skrivas som en funktion av $x$ som

$\displaystyle A\left(x\right) = 3x^2 \sin \alpha$

Sedan kan vi använda cosinussatsen på $a$, som ger oss att

$a^2 = 13x^2 - 12x^2\cos \alpha$ 

Vi löser ut $\cos \alpha$ och använder förhållandet $\sin \alpha = \pm \sqrt{1-\cos^2 \alpha}$

Insättning i $A(x)$ ger oss (arean måste vara positiv)

$\displaystyle A\left(x\right)=3x^2\sqrt{1-\left(\frac{13x^2-a^2}{12x^2}\right)^2}$

Detta ska vara exakt samma funktion som man får fram från herons formel då cosinussatsen och herons är besläktade. Denna funktion kan man sedan maximera. 

Herons formel fås genom att kombinera areasatsen, trig:ettan och cosinussatsen (och dessa finns i Ma3c faktiskt).

Givet att triangeln har sidorna $a$, $2x$ och $3x$ så ger areasatsen att
$A(x) = \frac{1}{2} 2x \cdot 3x \cdot \sin v = 3x^2 \sin v$,
där vinkeln $v$ ligger mellan sidorna $2x$ och $3x$.

Enligt cosinussatsen är 
$a^2 = (2x)^2 + (3x)^3 - 2\cdot 2x \cdot 3x \cdot \cos v$,  så  $\cos v = \dfrac{a^2 - 13x^2}{12x^2}$.

Här ser man att rimlighetsvillkoret $-1 < \cos v < 1$ är uppfyllt endast om $a/5 < x < a$. Här ser man alltså definitionsmängden för funktionen $A(x)$ vars maximum sökes.

Enligt trigonometriska ettan är
$\sin^2 v + \cos^2 v = 1$,  så  $\sin v = \sqrt{1 - (\dfrac{a^2 - 13x^2}{12x^2})^2 } = \dfrac{\sqrt{26 a^2 x^2 - 25 x^4 -a^4}}{12x^2}$

Detta sätts in i $A(x)$ som fåtts via areasatsen:
$A(x) = 3x^2 \cdot \dfrac{\sqrt{26 a^2 x^2 - 25 x^4 -a^4}}{12x^2} = \dfrac{1}{4} \sqrt{26 a^2 x^2 - 25 x^4 -a^4}$.

Det återstår att hitta maximumet för uttrycket $- 25 x^4 + 26 a^2 x^2 -a^4$. Substitutionen $t = x^2$ ger ett andragradsuttryck $g(t) = - 25 t^2 + 26 a^2 t -a^4$, vars maximum bestäms genom att lösa ekvationen $g^\prime(t) = 0$, d.v.s. $-50 t + 26a^2 = 0$, så $t = 13 a^2 / 25$, så $x^2 = 13a^2/25$, så $x = \sqrt{13}a /5$.

Detta värde på $x^2$ sätts in i $A(x) = \dfrac{1}{4} \sqrt{26 a^2 x^2 - 25 x^4 -a^4}$, vilket ger

$A( \sqrt{13}\,a/5 ) = \dfrac{1}{4} \sqrt{26 a^2 \cdot 13a^2/25 - 25 \cdot 169\,a^4/625 - a^4} = \dfrac{1}{4}\,\sqrt{144 a^4 / 25} = \dfrac{1}{4}\cdot \dfrac{12\,a^2}{5} = \dfrac{3\,a^2}{5}$.

Metoder från Matematik 4 räcker, men uppgiften (som den är formulerad) är på en helt galet hög svårighetsnivå.

Tack alla för bra och uttömmande svar!

Svaneke skrev:

Tack alla för bra och uttömmande svar!

Går att göra mkt enklare. Pythagoras' x2.