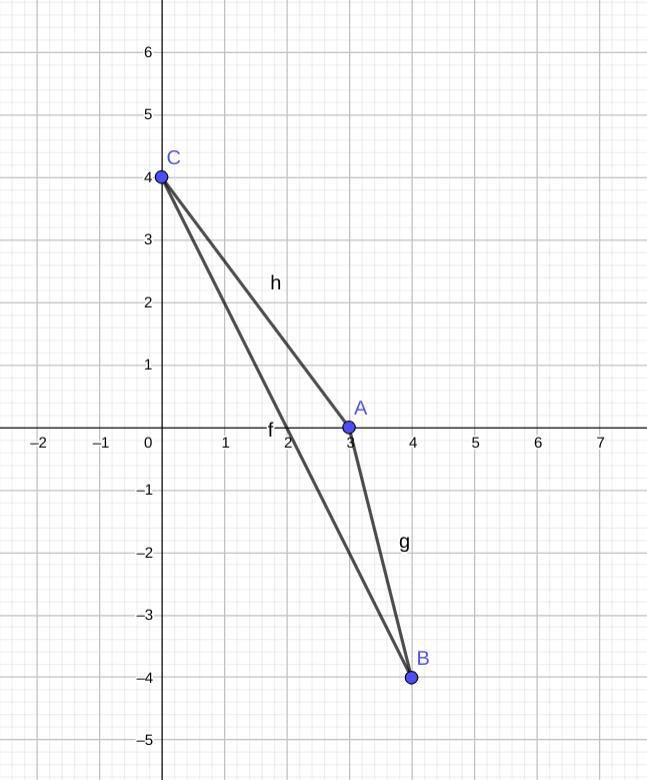
I vilken punkt skär höjden från hörnet A motstående sida?

Det är inte säkert att höjden skär mittpunkten.

Rita en figur och visa oss.

OK snyggt.

Kan du nu även rita in höjden mot A?

Tips: Höjden är vinkelrät mot BC.

Såhär?

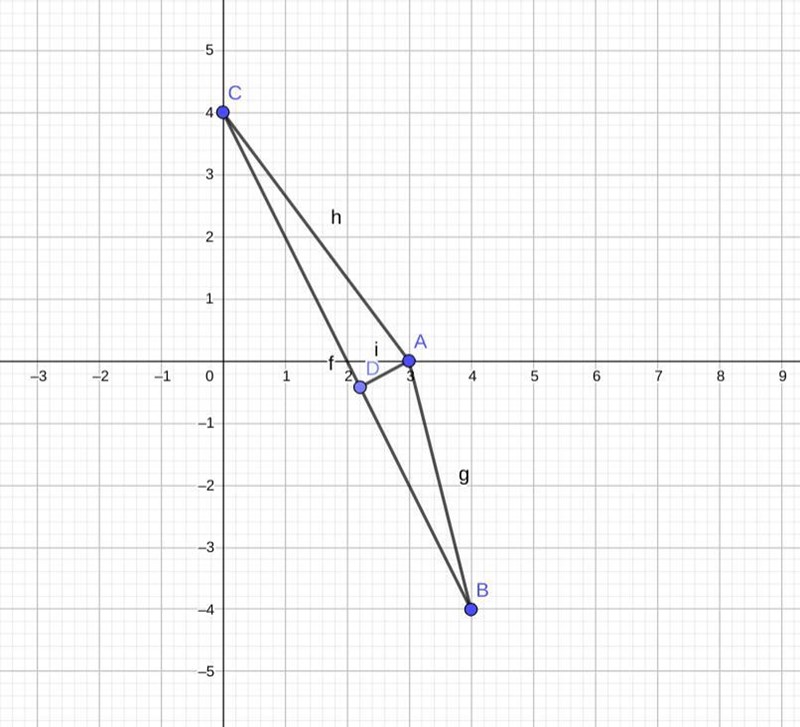
Ja. Snyggt.

Nu ska du ta reda på koordinaterna för skärningspunkten.

Då vore det ju bra att känna till ekvationen för linjen som BC sammanfaller med och ekvationen för linjen som höjden sammanfaller med, eller hur? 

Hur räknar man ut det?

Tips: utnyttja att höjden alltid är vinkelrät mot basen. Om du visste vad riktningskoefficienten för linjen genom punkterna B och C var, så skulle du kunna räkna fram riktningskoefficienten för triangelns höjd, eller hur?

Kalla ekvationerna $y=k_1x+m_1$ och $y=k_2x+m_2$

För den ena linjen känner du till de två punkterna B och C. Därmed kan du räkna ut linjens lutning $k_1$. Eftersom du vet var linjen skär $y$-axeln kan du direkt bestämma $m_1$.

För den andra linjen vet du att den är vinkelrät mot den första, vilket ger dig linjens lutning $k_2$ eftersom det för två vinkelräta linjer gäller att $k_1\cdot k_2=-1$. Du kan sedan beräkna $m_2$ genom att du känner till en punkt på linjen, nämligen punkt A.