Icke slutna kurvor med Green och Stoke
Hej!
Jag har inte fattat hur man använder greens formel och stokes sats på icke slutna kurvor. Jag fattar att en uppdelning behövs, men fattar inte hur man gör.
Hur tar man sig tillväga? Eller finns det något bra ställe på nätet som förklarar metodiken på ett förståerligt sätt.? ):
Det brukar se ut såhär:
Man har en arbetsintegral över en konstig kurva som söks. Om vektorfältet som utför arbetet är i 3 dimensioner används Stokes sats där randen på området är det viktiga. Två helt olika ytor kan kräva samma arbete om de har samma rand. När man delar upp ett området så är det randen man tar hänsyn till. Exempelvis kan en sluten cylinder beräknas med 3 kurvintegraler: 2 för locken och 1 för sidan.
Ett specialfall av Stokes sats är Greens sats som är applicerbar när vektorfältet råkar vara i 2D. Här blir det:
[Det som söks (svår)] + [kurvstycke(n)] = [Greens]
För att använda Greens krävs att kurvan är sluten. När du inser att du har en svår arbetsintegral vill du alltså skapa ett område genom att lägga till kurvstycken. Det viktiga här är att du skapar ett område som är lätt integrera över (i Greens) och att dina kurvstycken är lätta att parametrisera. Detta ger:
[Svår integral] = [Greens (lätt)] - [kurvstycken (lätt)]
,vilket är en ”lätt” ekvation.
Notera att Greens och Stokes har andra specifika krav sett till orientering som behöver följas.
Jag har fattat att när du har en icke-sluten kurva och vill använda Green's sats, så kan du skapa ett område genom att lägga till extra kurvstycken (kurvintegraler ?) så att du får en sluten kurva. När kurvan är sluten, kan du använda Green's sats på hela området, som om kurvan vore sluten från början. Sedan, för att få den ursprungliga linjeintegralen över den icke-slutna kurvan, subtraherar du helt enkelt de extra kurvstyckenas integraler från resultatet av Green's sats på den slutna kurvan. Så, i princip beräknar du Green's sats för den sluta kurvan och drar bort de delar som inte ingår i den ursprungliga icke-slutna kurvan.
Dock fattar jag inte riktigt hur man tolkar dem delar som "inte ingår" i kurvan. Hur ser jag det i en upg? Får jag bara lära mig att se det självt?
Till exempel funktionen x2 plus y2 = 1. Likhetstecknet medger att det är endast randen som "gills". Hur tänker jag här, vid tillämpning av greens eller stoke?
"Dock fattar jag inte riktigt hur man tolkar dem delar som "inte ingår" i kurvan. Hur ser jag det i en upg? Får jag bara lära mig att se det självt?"
Angående den här biten brukar det vara att man själv väljer hur man vill utöka kurvan, det finns trots allt många sätt att sätta ihop kurvan på, men vissa sätt kommer ge enklare areor och kurvintegraler. Tänk dig att vi ska räkna med ett vektorfält över kurva 1 och vill använda greens sats. Två sätt att bilda den slutna kurvan skulle kunna vara att göra utökningen mha kurva 2 eller att fortsätta på cirkeln tills den sluts med kurva 3.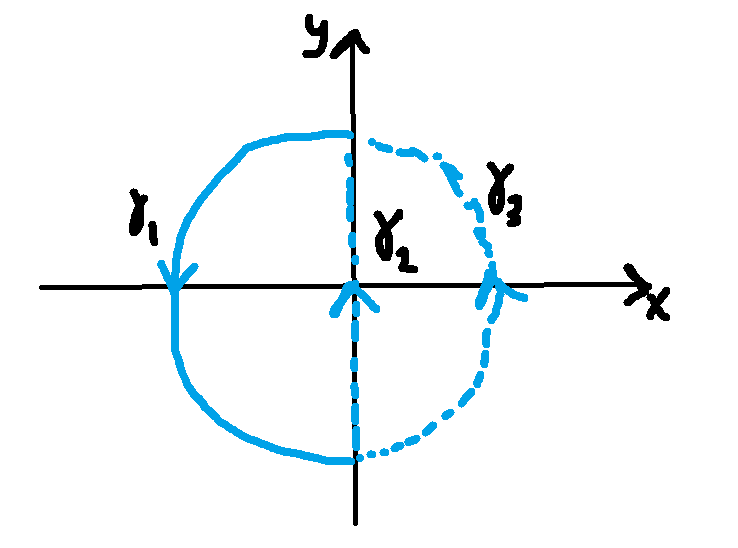
Jaha!
Så du menar att när man har en icke-sluten kurva och vill använda Green's sats, kan man välja olika sätt att sluta kurvan genom att lägga till extra kurvstycken, och detta val påverkar hur lätt beräkningarna blir. Till exempel, om man har en kurva 1 och vill sluta den med kurva 2 (en rak linje) eller fortsätta med en cirkulär kurva 3 för att stänga den, så ger dessa olika alternativ olika typer av områden.
Får helt enkelt träna på vad som blir enklast. Tack för hjälpen!



