Illustrera lösningarna.

Prova att skriva båda led på polär form. 

Menar du: z³ = r³ (cos (3v) + i sin (3v))

Ja, och hur blir HL?

$27i = 27\left(\cos \right(3v) + i \sin (3v\left)\right)$

Prova att sätta $z^3$ med basen $e$

Porkshop skrev:

Prova att sätta $z^3$ med basen $e$

 $e =27(\cos 90° + i \sin 90°)$

Varför bör jag göra det?

Andra sidan, e^ix = cosx + isinx

$e^{i90°}= \cos 90° + i \sin 90°$

Eller bli det:

 $e^{i\frac{\mathrm{\pi }}{2}}= \cos \frac{\mathrm{\pi }}{2} + i \sin \frac{\mathrm{\pi }}{2}$

Sista raden är rätt. Glöm inte perioden, +2pi*n. Kan du skriva om den nya till någonting upphöjt till 3 sen?

$någonting = \frac{\mathrm{\pi }}{2} + 2\mathrm{\pi } * \mathrm{n}$

Se det såhär:

$z^3=r^3{e}^{i3\alpha }$ där r är absolutbeloppet

Du kan då sätta en likhet mellan $3\alpha$ och argumentet till $z$ och en likhet mellan $r^3$ och absolutbeloppet.

Hänger du med?

Edit:

$r^3{e}^{i3\alpha }=r^3\left(\cos \right(3\alpha )+i\sin (3\alpha \left)\right)$

Porkshop skrev:

Se det såhär:

$z^3=r^3{e}^{i3\alpha }$ där r är absolutbeloppet

Du kan då sätta en likhet mellan $3\alpha$ och argumentet till $z$ och en likhet mellan $r^3$ och absolutbeloppet.

Hänger du med?

Edit:

$r^3{e}^{i3\alpha }=r^3\left(\cos \right(3\alpha )+i\sin (3\alpha \left)\right)$

Okej, då förstår jag det som att det är likheten till substitutionen som jag gjorde?

Vilken? Menar du

 $e^{\frac{i\mathrm{\pi }}{2}}=\cos \left(\frac{\mathrm{\pi }}{2}\right)+i\sin \left(\frac{\mathrm{\pi }}{2}\right)$

Porkshop skrev:

Vilken? Menar du

 $e^{\frac{i\mathrm{\pi }}{2}}=\cos \left(\frac{\mathrm{\pi }}{2}\right)+i\sin \left(\frac{\mathrm{\pi }}{2}\right)$

 Ne jag tänkte helt knasigt. Jag tror jag får testa göra om allt från början imorgon och har då förhoppningsvis bättre frågor :)

$$\begin{gathered} z^3 = 27i \\ {z}^3 = r^3(\cos 3v + i \sin 3v) \\ {z}^3 = 27(\cos 90° + i \sin 90°) \\ {e}^{\frac{\mathrm{\pi }}{2}i}= \frac{\mathrm{\pi }}{2} + 2\mathrm{\pi } * \mathrm{n} \end{gathered}$$

Hit kommer jag sen tar det stopp. Jag börjar tveka på om jag faktiskt förstår vad jag gör också.

Sista raden stämmer inte, men det gör inget. Du kan ta HL på rad 2 och jämföra med HL på rad 3. De liknar varann så mycket att du direkt får ut r och v. 

Laguna skrev:

Sista raden stämmer inte, men det gör inget. Du kan ta HL på rad 2 och jämföra med HL på rad 3. De liknar varann så mycket att du direkt får ut r och v. 

 Ja jag har kommit fram till detta:

$$\begin{gathered} VL=HL \\ {r}^3=27 \Rightarrow r=3 \\ Och \\ \cos 3v = \cos \frac{\mathrm{\pi }}{2} \end{gathered}$$

Det du vill utnyttja för vinkeln är (x^a)^b=x^a*b. Så bryt ut en trea från pi/2+2pi*n

Corokia cotoneaster skrev:

$$\begin{gathered} z^3 = 27i \\ {z}^3 = r^3(\cos 3v + i \sin 3v) \\ {z}^3 = 27(\cos 90° + i \sin 90°) \\ {e}^{\frac{\mathrm{\pi }}{2}i}= \frac{\mathrm{\pi }}{2} + 2\mathrm{\pi } * \mathrm{n} \end{gathered}$$

Hit kommer jag sen tar det stopp. Jag börjar tveka på om jag faktiskt förstår vad jag gör också.

Du skrev i inledningen att du har börjat kolla på de Moivres formel. Eftersom det är just den du ska använda här så är det bra om du förstår den.

Läs avsnittet jag länkade till och fråga här om det som är oklart.

Kort sammanfattning:

Om $z=|z|(\cos (v)+i\sin (v))$ så är

$z^n=|z|^n(\cos (nv)+i\sin (nv))$, där $\left|z\right|=Abs\left(z\right)$ och $v=Arg\left(z\right)$.

För $n=3$ gäller alltså

$z^3=|z|^3(\cos (3v)+i\sin (3v))$.

Ser du likheterna med din ekvation?

Yngve skrev:

Corokia cotoneaster skrev:

$$\begin{gathered} z^3 = 27i \\ {z}^3 = r^3(\cos 3v + i \sin 3v) \\ {z}^3 = 27(\cos 90° + i \sin 90°) \\ {e}^{\frac{\mathrm{\pi }}{2}i}= \frac{\mathrm{\pi }}{2} + 2\mathrm{\pi } * \mathrm{n} \end{gathered}$$

Hit kommer jag sen tar det stopp. Jag börjar tveka på om jag faktiskt förstår vad jag gör också.

Du skrev i inledningen att du har börjat kolla på de Moivres formel. Eftersom det är just den du ska använda här så är det bra om du förstår den.

Läs avsnittet jag länkade till och fråga här om det som är oklart.

 

Kort sammanfattning:

Om $z=|z|(\cos (v)+i\sin (v))$ så är

$z^n=|z|^n(\cos (nv)+i\sin (nv))$, där $\left|z\right|=Abs\left(z\right)$ och $v=Arg\left(z\right)$.

 

För $n=3$ gäller alltså

$z^3=|z|^3(\cos (3v)+i\sin (3v))$.

Ser du likheterna med din ekvation?

 Ja nu blev det lättare :)

$$\begin{gathered} z^3 = 3^3\left(\cos 3\right(90°) + i \sin 3(90°\hspace{0.17em}\left)\right) \\ {z}^3= 3^3(\cos 270° + i \sin 270°) \end{gathered}$$

Corokia cotoneaster skrev:

$$\begin{gathered} z^3 = 3^3\left(\cos 3\right(90°) + i \sin 3(90°\hspace{0.17em}\left)\right) \\ {z}^3= 3^3(\cos 270° + i \sin 270°) \end{gathered}$$

 Ja nästan.

Formeln lyder $z^3=|z|^3(\cos (3v)+i\sin (3v))$

Din ekvation lyder $z^3=27(\cos (90)+i \sin (90))$

Det betyder att

• $|z|^3=27$

och att

• $3v=90+n\cdot 360$

Vad finns det då för möjliga värden på $v$?

$$\begin{gathered} z^3 = 3^3 (\cos 90° + i \sin 90°) \\ {z}^3 = 27(\cos 90 ° + i \sin 90°) \\ 3v = 27(\cos 90°+ i \sin 90°) \\ v = 9 ( \cos 30° + i \sin 30°) \\ v = 9 (\cos \frac{\mathrm{\pi }}{6} + i \sin \frac{\mathrm{\pi }}{6} + n * 2\mathrm{\pi }) \end{gathered}$$

Corokia cotoneaster skrev:

$$\begin{gathered} z^3 = 3^3 (\cos 90° + i \sin 90°) \\ {z}^3 = 27(\cos 90 ° + i \sin 90°) \\ 3v = 27(\cos 90°+ i \sin 90°) \\ v = 9 ( \cos 30° + i \sin 30°) \\ v = 9 (\cos \frac{\mathrm{\pi }}{6} + i \sin \frac{\mathrm{\pi }}{6} + n * 2\mathrm{\pi }) \end{gathered}$$

 Nej nu är det jätterörigt. v är argumentet till $z$, dvs en vinkel. Du har skrivit v som ett komplext tal på de 3 sista raderna.

Kan du lösa följande två ekvationer?

1. $r^3=27$
2. $3v=90+n\cdot 360$

Här har jag kallat absolutbeloppet av $z$ (dvs $|z|$) för $r$ och argumentet till $z$ för $v$.

Dessutom har jag infört heltalet $n$ för att hitta alla vinklar.

Yngve skrev:

Corokia cotoneaster skrev:

$$\begin{gathered} z^3 = 3^3 (\cos 90° + i \sin 90°) \\ {z}^3 = 27(\cos 90 ° + i \sin 90°) \\ 3v = 27(\cos 90°+ i \sin 90°) \\ v = 9 ( \cos 30° + i \sin 30°) \\ v = 9 (\cos \frac{\mathrm{\pi }}{6} + i \sin \frac{\mathrm{\pi }}{6} + n * 2\mathrm{\pi }) \end{gathered}$$

 Nej nu är det jätterörigt. v är argumentet till $z$, dvs en vinkel. Du har skrivit v som ett komplext tal på de 3 sista raderna.

Kan du lösa följande två ekvationer?

1. $r^3=27$
2. $3v=90+n\cdot 360$

Här har jag kallat absolutbeloppet av $z$ (dvs $|z|$) för $r$ och argumentet till $z$ för $v$.

Dessutom har jag infört heltalet $n$ för att hitta alla vinklar.

 $$\begin{gathered} 1. r^3= 27 \\ r = {27}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.} \\ r= 3 \\ 2. = 3v = 90° + n * 360° \\ v = 30° + n * 120° \end{gathered}$$

Corokia cotoneaster skrev:

$$\begin{gathered} 1. r^3= 27 \\ r = {27}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.} \\ r= 3 \\ 2. = 3v = 90° + n * 360° \\ v = 30° + n * 120° \end{gathered}$$

 Bra!

Nu har du bestämt absolutbeloppet av z  och alla möjliga argument till z.

Vilka av dessa argument (vinklar) ligger i intervallet 0° till 360°?

Yngve skrev:

Corokia cotoneaster skrev:

$$\begin{gathered} 1. r^3= 27 \\ r = {27}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.} \\ r= 3 \\ 2. = 3v = 90° + n * 360° \\ v = 30° + n * 120° \end{gathered}$$

 Bra!

Nu har du bestämt absolutbeloppet av z  och alla möjliga argument till z.

Vilka av dessa argument (vinklar ligger i intervallet 0° till 360°?

 tänkte du att jag ska sätta n = 0,1,2,3? :)

Nej det bli 0,1 och 2

Corokia cotoneaster skrev:

Nej det bli 0,1 och 2

 Ja. Det ger dig alltså 3 möjliga värden på vinkeln v som alla uppfyller ekvationen.

Dina nästa steg blir:

1. Ta fram dessa vinklar.
2. Konstruera de 3 komplexa talen som hör till.
3. Kontrollera att alla dessa tal uppfyller ursprungsekvationen $z^3=27i$
4. Illustrera (dvs rita ut) lösningarna i det komplexa talplanet.

Visa dina resultat här.

Menar du såhär:

$$\begin{gathered} n=0 \\ v = \cos 30° + i\sin 30° +0 * 120° = \end{gathered}$$

om jag omvandlar till radianer får jag det till detta:

$v = \frac{\sqrt{3}}{2} + \frac{1}{2}i$

Vad gör jag med detta?

Corokia cotoneaster skrev:

Menar du såhär:

$$\begin{gathered} n=0 \\ v = \cos 30° + i\sin 30° +0 * 120° = \end{gathered}$$

 Nej inte alls. Du skriver att v är ett komplext tal.

v är en vinkel, inte ett komplext tal.

(Jag skriver alla vinklar i grader här.)

• Om $n=0$ så är $v=30$. Motsvarande komplexa tal är $z_1=3(\cos (30)+i\sin (30))$.
• Om $n=1$ så är $v=30+1\cdot 120=150$. Motsvarande komplexa tal är $z_2=3(\cos (150)+i\sin (150))$.
• Om $n=2$ så är $v=30+2\cdot 120=270$. Motsvarande komplexa tal är $z_3=3(\cos (270)+i\sin (270))$.

Så. Nu har jag gjort steg 1 och 2 åt dig. Kan du fortsätta med steg 3 och 4?

En fråga bara. Vill du att jag ska multiplicera in 3:an i parantesen för att se om ekvationen uppfyller ursprungsekvationen?

Alltså såhär:

$$\begin{gathered} z_1=3(\cos 30° + i \sin 30°) = \cos (90°) + 3i \sin (90°) = 0 + 3i + 1 \\ = 1+3i \end{gathered}$$

FCorokia cotoneaster skrev:

En fråga bara. Vill du att jag ska multiplicera in 3:an i parantesen för att se om ekvationen uppfyller ursprungsekvationen?

Alltså såhär:

$$\begin{gathered} z_1=3(\cos 30° + i \sin 30°) = \cos (90°) + 3i \sin (90°) = 0 + 3i + 1 \\ = 1+3i \end{gathered}$$

Nej, jag vill att du använder de Moivres formel för att ta reda på om $z_1=3(\cos (30)+i\sin(30))$ uppfyller ekvationen $z^3=27i$.

Dvs använd de Moivres formel för att ta fram ett uttryck för $z_1^3$ och jämför sedan detta uttryck med $27i$.

Och jag vill att du sedan gör samma sak även för $z_2$ och $z_3$.

-------------

Och du gör fel när du multiplicerar in trean.

$3\cdot \cos (30)\neq\cos (90)$ och 

$3\cdot i\sin (30)\neq 3i\sin (90)$

Yngve skrev:

FCorokia cotoneaster skrev:

En fråga bara. Vill du att jag ska multiplicera in 3:an i parantesen för att se om ekvationen uppfyller ursprungsekvationen?

Alltså såhär:

$$\begin{gathered} z_1=3(\cos 30° + i \sin 30°) = \cos (90°) + 3i \sin (90°) = 0 + 3i + 1 \\ = 1+3i \end{gathered}$$

Nej, jag vill att du använder de Moivres formel för att ta reda på om $z_1=3(\cos (30)+i\sin(30))$ uppfyller ekvationen $z^3=27i$.

Dvs använd de Moivres formel för att ta fram ett uttryck för $z_1^3$ och jämför sedan detta uttryck med $27i$.

Och jag vill att du sedan gör samma sak även för $z_2$ och $z_3$.

-------------

Och du gör fel när du multiplicerar in trean.

$3\cdot \cos (30)\neq\cos (90)$ och 

$3\cdot i\sin (30)\neq 3i\sin (90)$

 Jag ska alltså ta denna formel: 

$z^{n }= \left(r\right(\cos v + i \sin v){)}^n = r^n(\cos nv + i \sin nv)$

Corokia cotoneaster skrev:

 Jag ska alltså ta denna formel: 

$z^{n }= \left(r\right(\cos v + i \sin v){)}^n = r^n(\cos nv + i \sin nv)$

 Ja.

$$\begin{gathered} n= 0 \\ {3}^n(\cos (n30°) + i \sin (n30°\left)\right) \\ {3}^0 ( \cos (0 *30°) + i sin (0 * 30°\left)\right) \\ 1(\cos (0°) + i \sin (0°\left)\right) \\ 1(1+i* 0) \\ 1\left(1\right) = 1 \end{gathered}$$

Blev detta verkligen rätt?

Corokia cotoneaster skrev:

$$\begin{gathered} n= 0 \\ {3}^n(\cos (n30°) + i \sin (n30°\left)\right) \\ {3}^0 ( \cos (0 *30°) + i sin (0 * 30°\left)\right) \\ 1(\cos (0°) + i \sin (0°\left)\right) \\ 1(1+i* 0) \\ 1\left(1\right) = 1 \end{gathered}$$

Blev detta verkligen rätt?

Nej det blev inte rätt. Exponenten du ska använda i de Moivres formel är 3 eftersom ekvationen du ska lösa är $z^3=27i$.

Du ska alltså använda att $z_1=3(\cos (30)+i\sin (30))$ och med hjälp av de Moivres formel bestämma $z_1^3$. Sedan ska du jämföra det uttrycket med $27i$.

Gör sedan samma sak med $z_2$ och $z_3$.

$$\begin{gathered} 3^3\left(\cos \right(3*30°) + i \sin (3*30°\left)\right) \\ 27( \cos (90°) + i \sin (90°\left)\right) \\ 27(0+i*1) \\ 27* i = 27i (stämmer bra) \\ {3}^3\left(\cos \right(3*150°) + i \sin (3*150°\left)\right) \\ 27\left(\cos \right(450°) + i \sin (450°\left)\right) \\ 27(0 + i *1) \\ 27* i = 27i \left(stämmer\right) \\ {3}^3\left(\cos \right(3*270°) + i \sin (3*270°\left)\right) \\ 27(\cos (810°) + i sion (810°\left)\right) \\ 27 ( 0 + i * 1) \\ 27 *i = 27i \left(stämmer\right) \end{gathered}$$

Corokia cotoneaster skrev:

$$\begin{gathered} 3^3\left(\cos \right(3*30°) + i \sin (3*30°\left)\right) \\ 27( \cos (90°) + i \sin (90°\left)\right) \\ 27(0+i*1) \\ 27* i = 27i (stämmer bra) \\ {3}^3\left(\cos \right(3*150°) + i \sin (3*150°\left)\right) \\ 27\left(\cos \right(450°) + i \sin (450°\left)\right) \\ 27(0 + i *1) \\ 27* i = 27i \left(stämmer\right) \\ {3}^3\left(\cos \right(3*270°) + i \sin (3*270°\left)\right) \\ 27(\cos (810°) + i sion (810°\left)\right) \\ 27 ( 0 + i * 1) \\ 27 *i = 27i \left(stämmer\right) \end{gathered}$$

OK bra, det stämmer. Det var steg 3.

Nu är det bara steg 4 kvar.

Ritade en bild tidigare idag när jag trodde att jag var klar, men då hade jag räknat i radianer. Bör jag rita en ny bild nu när jag har räknat i grader eller duger denna?

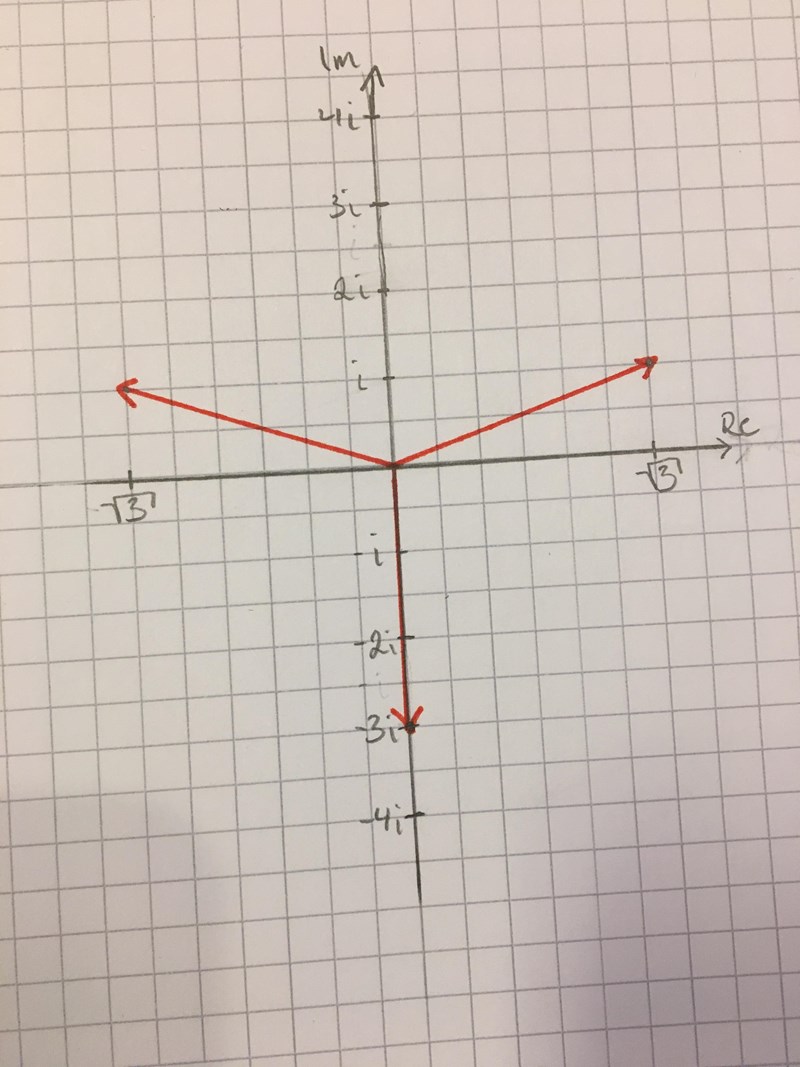
Corokia cotoneaster skrev:

Ritade en bild tidigare idag när jag trodde att jag var klar, men då hade jag räknat i radianer. Bör jag rita en ny bild nu när jag har räknat i grader eller duger denna?

Snygg bild!

Lösningen med argumentet 270° är rätt, men de andra två är inte rätt.

Dubbelkolla real- och imaginärdelarna för dessa lösningar.

Det spelar ingen roll om du räknar vinklar i grader eller radianer här.

Yngve skrev:

Corokia cotoneaster skrev:

Ritade en bild tidigare idag när jag trodde att jag var klar, men då hade jag räknat i radianer. Bör jag rita en ny bild nu när jag har räknat i grader eller duger denna?

Snygg bild!

Lösningen med argumentet 270° är rätt, men de andra två är inte rätt.

Dubbelkolla real- och imaginärdelarna för dessa lösningar.

Det spelar ingen roll om du räknar vinklar i grader eller radianer här.

 

 Jag förstår inte vad som är fel? Det enda jag märkte är att mitt minustecken framför $\sqrt{3}$ knappt syns

Sen menade jag om det gör något om själva uträkningen är i grader men bilden är i radianer. har inte kvar det jag gjorde i radianer. Isf är det ju lättare att göra en ny bild, eftersom denna ändå var fel?

Om du räknat i grader, bör bilden också visa i grader. Detsamma gäller i radianer.

Porkshop skrev:

Om du räknat i grader, bör bilden också visa i grader. Detsamma gäller i radianer.

 Det jag missänkte, fastnar på hur jag ska göra den dock :(

Gör likadant som du gjorde, fast med radianer istället. 

Eller omvandla radianerna till grader.

Jag får inte till det, det blir ju liksom inte lika, i radianer kom jag ju fram till tex, $\sqrt{3}+i$ när n=0

Men nu har jag, $3\left(\cos \right(30°) + i \sin (30°\left)\right)$

Ska jag sätta ut $30° på Re axe\ln och i på im-axe\ln ?$

Jag skulle rekommendera att du gör om uppgiften I radianer istället så att du lär dig, I fortsättningen räknar du endast I radianer.

Du började med $z^3=27i$

Sätt $z = r\left(\cos \right(v)+i\sin (v\left)\right)$

vad är $z^3$?

Jag tror faktiskt inte att jag orkar gör om denna igen! Den har tagit två dagar nu.

Jag har ju redan räknat den i radianer en gång. Problemet nu är att illustrera den i det komplexa talplanet i grader.

Ok, vill du att jag ska skicka en vägledning?

Porkshop skrev:

Ok, vill du att jag ska skicka en vägledning?

 Ja gärna :)

I bilden finns inga utskrivna vinklar, så det spelar ingen roll alls om du har använt grader eller radianer.

Att $\sqrt{3}$+i är fel ser du om du tar beloppet: det blir 2, men det ska bli 3.

Laguna skrev:

I bilden finns inga utskrivna vinklar, så det spelar ingen roll alls om du har använt grader eller radianer.

Att $\sqrt{3}$+i är fel ser du om du tar beloppet: det blir 2, men det ska bli 3.

 Det är nog jag som skrev fel. Det ska vara $\frac{3}{2}\left(\sqrt{3} + i\right)$ Men det spelar ingenroll nu när jag har gjort uppgiften i grader och ska rita en ny bild

Ok, kolla här:

 $z^3 = 27i$ = $r^3\left(\cos \right(3v)+i\sin (3v\left)\right)$

Eftersom att $z =r\left(\cos \right(v)+i\sin (v\left)\right)$ (standard polär form)

Där  $r = \left|z\right|$

$\left|27i\right| =\sqrt{{27}^2}=27$

Därmed är $r^3=27 \iff r =3$

Då behöver vi bara ta reda på argumentet till $z^3$

$z^3=27i =27\left(i\right) =27(\cos \frac{\mathrm{\pi }}{2}+i\sin (\frac{\mathrm{\pi }}{2}\left)\right)$

Då får vi $3v=\frac{\mathrm{\pi }}{2}+2\mathrm{\pi n} \iff \mathrm{v}=\frac{\mathrm{\pi }}{6}+\frac{2\mathrm{\pi n}}{3}$ Där $n$ antingen är 0, 1 eller 2

Då får du $$\begin{gathered} z_1=3\left(\cos \right(\frac{\mathrm{\pi }}{6})+i\sin (\frac{\mathrm{\pi }}{6}\left)\right) =3(\frac{\sqrt{3}}{2}+\frac{1}{2}i) \\ Jag orkar inte skriva alla lösningar, men du ser mönstrer \end{gathered}$$

Om du någonstans inte hänger med, skriv

Är det bättre att gör någonting såhär så att man på ett ungefär kan rita ut graderna efter cirkeln som i enhetscirkeln?

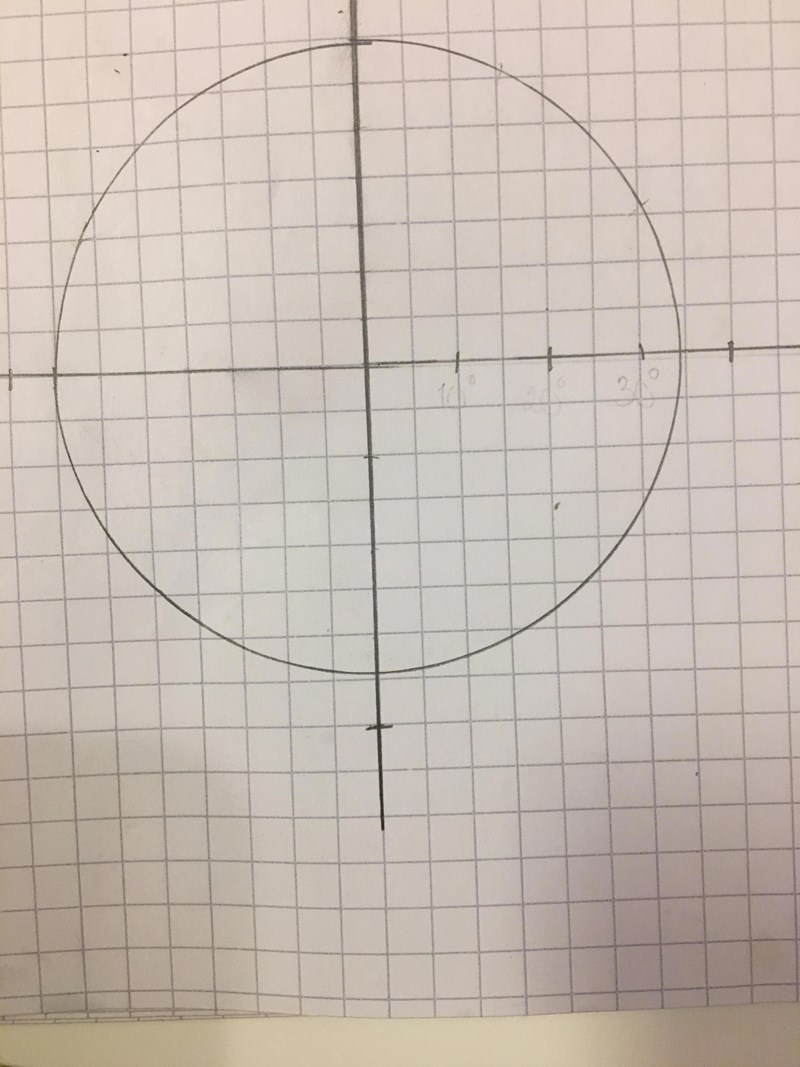
Var ligger $\frac{1}{2}$? vektorn ska vara 3ggr så lång

Porkshop skrev:

Var ligger $\frac{1}{2}$? vektorn ska vara 3ggr så lång

 Tänkte du på im eller Re?

Funkar inte detta?

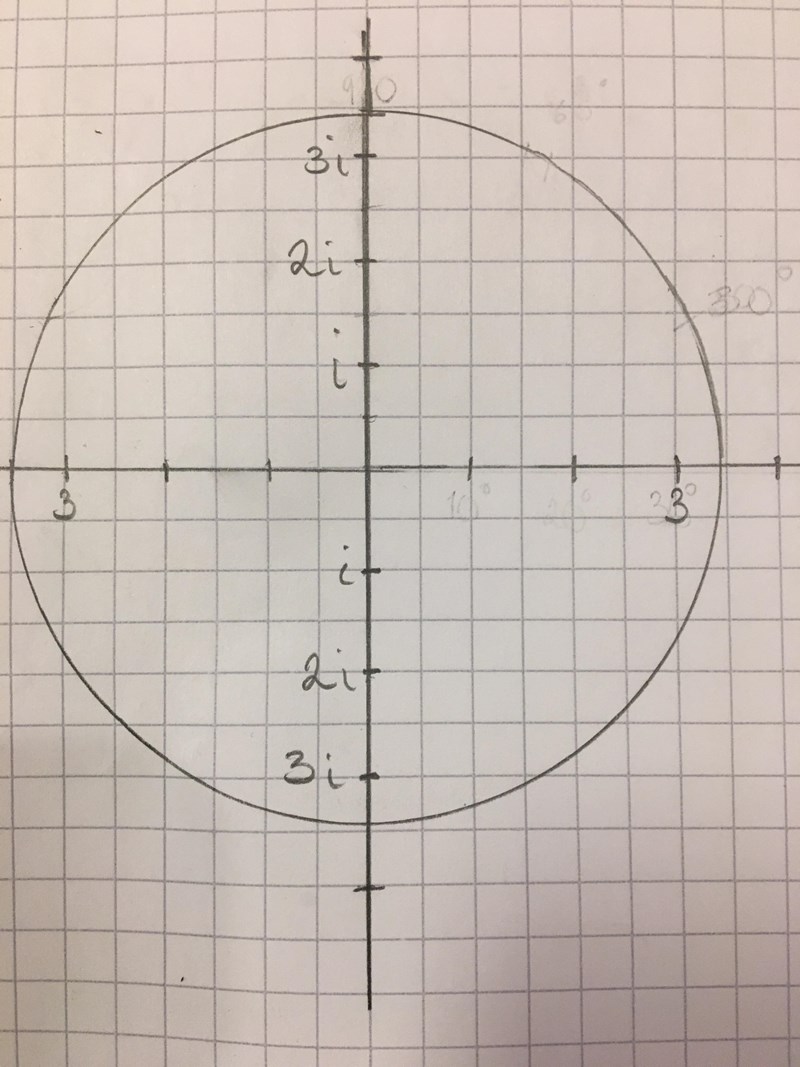
Nu har jag inte ritat klart den då jag inte vet om jag är på rätt spår ännu.

Jo, men cirkeln ska fortfarande ha radien 1 medans $z$ ska vara utanför

Gjorde en ny som har radien 1:

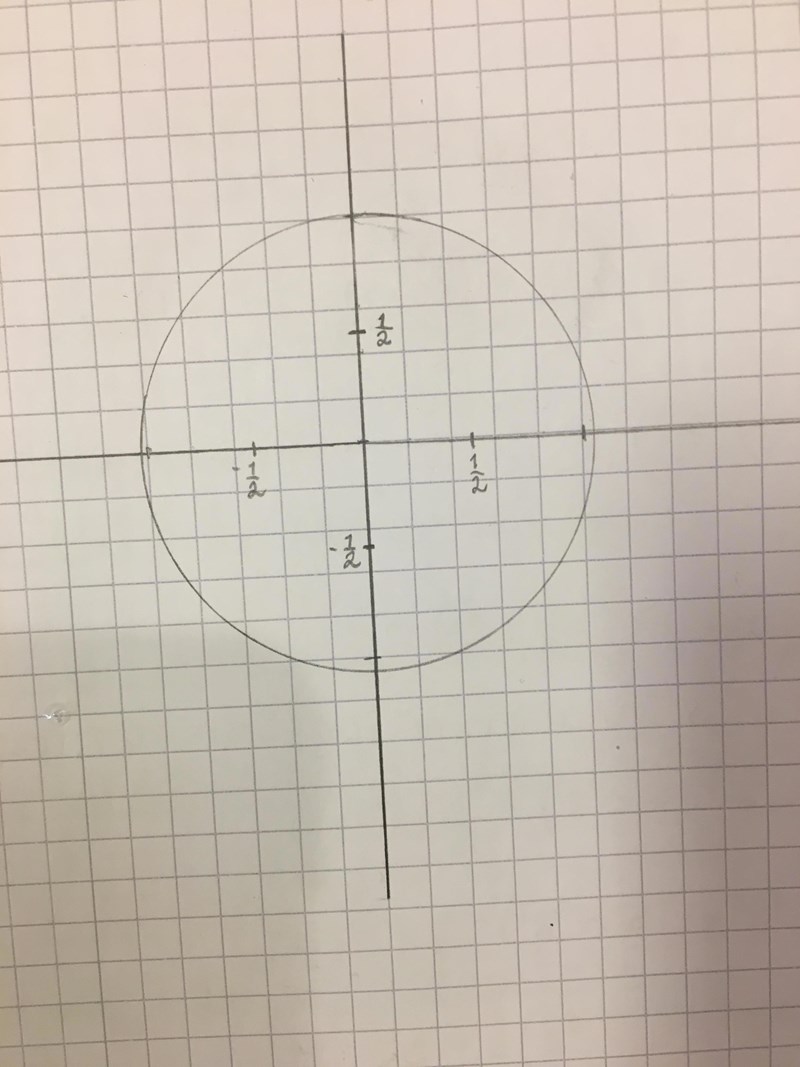
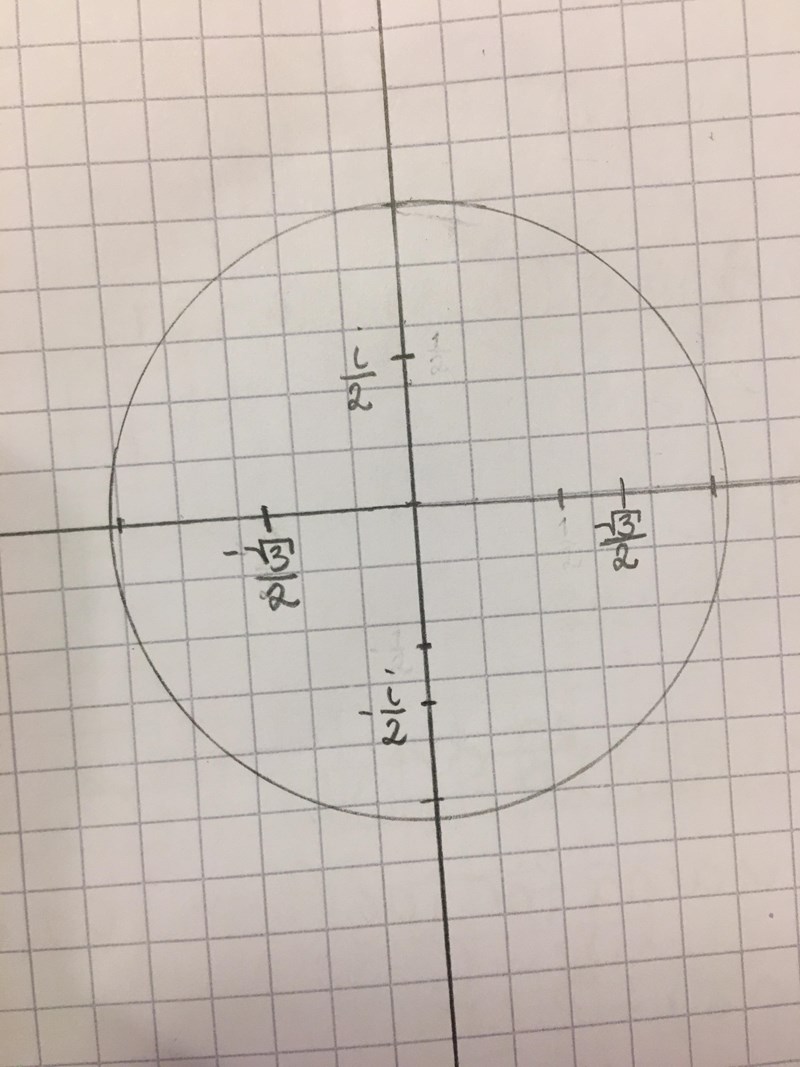
Pricka nu i sqrt(3)/2 och i/2

Porkshop skrev:

Pricka nu i sqrt(3)/2 och i/2

 Vad betyder det där? 

Jag har även hela min uträkning i grader.

sqrt = roten ur. Jag kan inte formera nu när jag är på min telefon.

Porkshop skrev:

sqrt = roten ur. Jag kan inte formera nu när jag är på min telefon.

 Okej, då blir det ju nästa som min förra.

Pricka nu ut Im(z) och Re(z) dra ett streck 3ggr så långt genom punkten från origo.

Vad menar du med strecken ?:) Förstod inte riktigt det

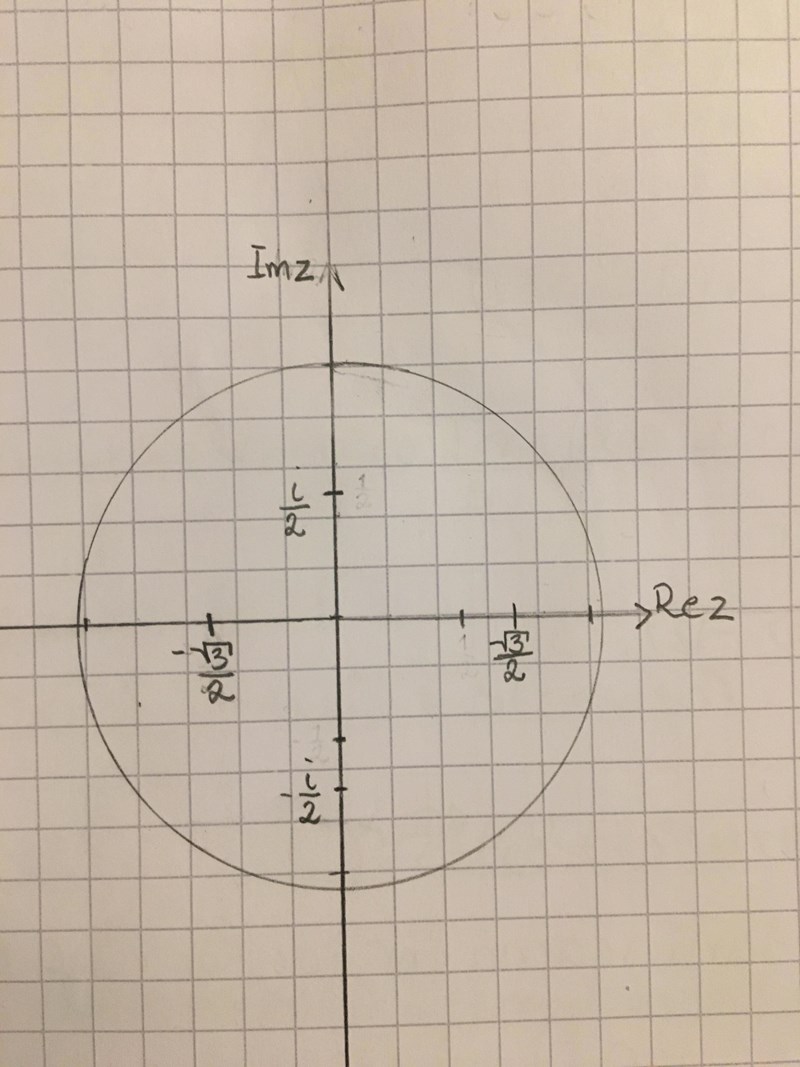
Hej igen.

Till att börja med - om du använder grader eller radianer spelar ingen roll.

Det gäller nämligen att cos(30°) är exakt samma tal som cos(pi/6), nämligen $\frac{\sqrt{3}}{2}$ och sin(30°) är exakt samma tal som sin(pi/6), nämligen $\frac{1}{2}$.

Det verkar som om du har missuppfattat detta med grader och radianer. Båda enheterna används för att mäta vinklar, på samma sätt som både enheterna centimeter och tum kan användas för att mäta sträckor.

Att trigonometriska funktioner som sinus och cosinus har värden som kan exakt uttryckas med hjälp av rotuttryck (ex som ovan) har ingenting att göra med om vinkeln är uttryckt i grader eller radianer. 

Vidare - om du ska markera det komplexa talet $3(\cos (30) + i\sin (30))$ i det komplexa talplanet så kan du göra på två olika sätt:

Metod 1. Använd polär form direkt, dvs rita en pil med längden 3 från origo i riktning 30°. Detta görs enklast genom att rita en cirkel med radie 3 (skippa alltså enhetscirkeln här, det är bara ett onödigt steg) runt origo och på den sätta ut en punkt som ligger 30° ovanför den horisontella axeln. På den cirkeln kan du sedan även markera de andra två lösningarna.

Metod 2. Gör om det komplexa talet till rektangulär form och pricka in realdel och imaginärdel för sig.

Eftersom $3(\cos (30) + i\sin (30))=$

$=3(\frac{\sqrt{3}}{2}+i\cdot\frac{1}{2})=$

$=\frac{3\sqrt{3}}{2}+i\cdot\frac{3}{2}\approx2,6+1,5i$

så är realdelen alltså cirka 2,6 och imaginärdelen lika med 1,5 och då är det bara att markera detta i det komplexa talplanet.

Tack för all hjälp! Och erat stora tålamod ☺️