Index notation
Hej, någon som kan förklara varför där jag markerade blir noll?
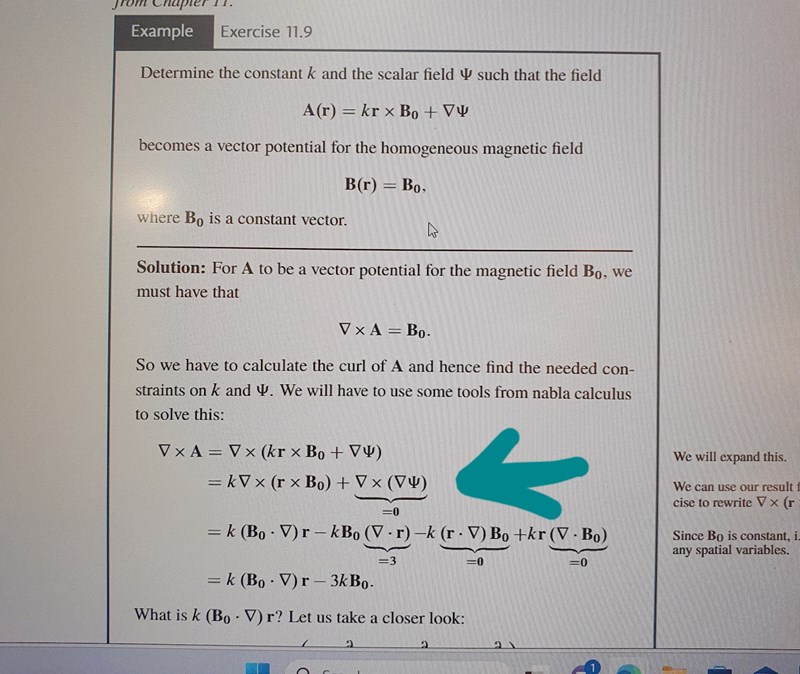
Rot(grad(A))=0 för alla skalärfält A. Detta eftersom att grad(A) är ett konservativt fält (med potential A) och rotationen av alla konservativa fält är 0. Tänk på en linjeintegral i ett konservativt fält. Alla kurvor från a till b kan ersättas med den raka sträckan från a till b.
Denna källa visar lite mer matematiskt varför det gäller.
Så där det står ∇ψbetyder det att ψär
en skalär potential??
Tillägg: 22 jan 2024 20:22
Såg att i fråga de står att ψ är en skalär fält vilket jag trodde att det är bara en konstant. Men här de menar att ψ är en skalär funktion ellehur?
Kan man säga att ett vekforfält kallas konservativ fält om det bildas/ härleds från gradienten av en skalärfunktion ex B= gradψ ?
Men vad är då vektor potential? Alltså jag märker man använder ordet vektor potential och sklär potential. Man säger t.ex om ∇XA =0 då har A skalär potenatial dvs A=∇Q och man vet även att A är konservativt.
Men om vektfältet A härleds av rotationen av en annan vektorfält dvs om A= ∇XB då är B vektorpotential till A samt ∇. A=0
Ja, om fältet kan skrivas som gradienten av ett skalär existerar en potential och fältet är konservativt.
Ett annat sätt att komma ihåg det är minnesregeln "∇×∇=0", vilket betyder att om man betraktar nablaoperatorn som en vektor så är kryssprodukten av en vektor med sig själv noll.
Med tanke på trådrubriken undrar jag dock om din första tanke var härleda det i indexnotation?
Aa exakt, man ska använda sig av index notation för att bestämma konstanten k och ψ
Några ledtrådar på vägen; man kan använda sig av att kryssprodukten mellan två vektorer kan uttryckas med hjälp av Levi-Civita-tensorn εijk så här
(r×B)i=εijkxjBk
Det finns ett väldigt nyttigt samband som kanske dyker upp under räkningarna i någon variant:
εumiεjki=δujδmk-δukδmj
Annat att ha i tankarna: ∂xj∂xk=δjk, samt δjj=3
Tack!
Jag kanske ska påpeka att din första fråga, dvs varför ∇×(∇f)≡0 också går att förklara i indexnotation.
Det bygger på symmetrin hos andraderivator vilket man brukar visa i den första kursen i flervariabelanalys. Det spelar ingen roll om man först deriverar en skalär funktion f(x,y) med avseende på x och sedan på y eller tvärtom:
∂2f∂x∂y =∂2f∂y∂x
Med indexnotation kan fältet ∇×F=∇×(∇f) uttryckas som
(∇×F)k=εijk∂Fj∂xi=εijk∂2f∂xi∂xj
Nu kan vi utnyttja att εijk=-εjik och skriva om det som en summa samt utnyttja att andraderivatan av en skalär är symmetrisk
εijk∂2f∂xi∂xj=12(εijk∂2f∂xi∂xj-εjik∂2f∂xi∂xj)=εijk12(∂2f∂xi∂xj-∂2f∂xj∂xi)≡0
Man kan på liknande sätt visa att detta gäller för alla symmetriska tensorer, dvs om du kontraherar en antisymemtrisk tensor, t.ex. εijk med en symmetrisk tensor blir slutresultatet alltid 0.
D4NIEL skrev:Jag kanske ska påpeka att din första fråga, dvs varför ∇×(∇f)≡0 också går att förklara i indexnotation.
Det bygger på symmetrin hos andraderivator vilket man brukar visa i den första kursen i flervariabelanalys. Det spelar ingen roll om man först deriverar en skalär funktion f(x,y) med avseende på x och sedan på y eller tvärtom:
∂2f∂x∂y =∂2f∂y∂x
Med indexnotation kan fältet ∇×F=∇×(∇f) uttryckas som
(∇×F)k=εijk∂Fj∂xi=εijk∂2f∂xi∂xj
Nu kan vi utnyttja att εijk=-εjik och skriva om det som en summa samt utnyttja att andraderivatan av en skalär är symmetrisk
εijk∂2f∂xi∂xj=12(εijk∂2f∂xi∂xj-εjik∂2f∂xi∂xj)=εijk12(∂2f∂xi∂xj-∂2f∂xj∂xi)≡0
Man kan på liknande sätt visa att detta gäller för alla symmetriska tensorer, dvs om du kontraherar en antisymemtrisk tensor, t.ex. εijk med en symmetrisk tensor blir slutresultatet alltid 0.
((∇×F)k=εijk∂Fj∂xi=εijk∂2f∂xi∂xjhur fick du det här?
Läste i en bok att "
∇ × (∇𝜙) ≡ 𝟎
för varje skalärfält 𝜙 (”ett potentialfält är alltid virvelfritt”)"
Menar de om 𝜙 är skalärfält då är dess potentialfält dvs ∇𝜙 virvelfrit? S
I am Me skrev:D4NIEL skrev:Jag kanske ska påpeka att din första fråga, dvs varför ∇×(∇f)≡0 också går att förklara i indexnotation.
Det bygger på symmetrin hos andraderivator vilket man brukar visa i den första kursen i flervariabelanalys. Det spelar ingen roll om man först deriverar en skalär funktion f(x,y) med avseende på x och sedan på y eller tvärtom:
∂2f∂x∂y =∂2f∂y∂x
Med indexnotation kan fältet ∇×F=∇×(∇f) uttryckas som
(∇×F)k=εijk∂Fj∂xi=εijk∂2f∂xi∂xj
Nu kan vi utnyttja att εijk=-εjik och skriva om det som en summa samt utnyttja att andraderivatan av en skalär är symmetrisk
εijk∂2f∂xi∂xj=12(εijk∂2f∂xi∂xj-εjik∂2f∂xi∂xj)=εijk12(∂2f∂xi∂xj-∂2f∂xj∂xi)≡0
Man kan på liknande sätt visa att detta gäller för alla symmetriska tensorer, dvs om du kontraherar en antisymemtrisk tensor, t.ex. εijk med en symmetrisk tensor blir slutresultatet alltid 0.
((∇×F)k=εijk∂Fj∂xi=εijk∂2f∂xi∂xjhur fick du det här?
Han definierade F som F=∇f, eftersom det är Fj vi tittar på blir det ∂f∂xj.
Menar de om 𝜙 är skalärfält då är dess potentialfält dvs ∇𝜙 virvelfrit?
Stämmer, ett fält F är virvelfritt just om rot(F)=0


