Induktion

Den sista termen skall vara $s^{n-1}$. Tryckfel i boken.

Kan du snälla kolla på andra eventuella tryckfell i den här rutan innan jag tar upp den igen?

dajamanté skrev :

Smutstvätt har försökt förklara för min induktion (i fysik2 också..). Jag tog upp boken och även där är jag ogenomtrånglig till förnuften.

Det börjar med: vi vet att $S_n=1+2+4+8+16+...+2n-1$?

Vad då? Hur vet vi? Hela denna listan har jämna tal, hur kan 2n-1 vara en jämn tal?

Jag har läst resten, men eftersom min hjärna fastnade på 2n-1, tog jag inget in....

$$\begin{gathered} S_n=\sum _{i=1}^n{2}^{i-1}=2n-1 \\ {S}_n=1+2+4+8+...2^{n-1} \end{gathered}$$

Hej!

Det är fel på nästan varje rad i bokens text! Vilken bok är det fråga om, så att jag ser till att undvika att den? Kan du skriva ner bokens ISBN-nummer?

Uppgiften skulle istället ha varit denna: Bevisa med matematisk induktion att formeln $S_n = \sum_{i=1}^{n}2^{n-1} = 2^{n}-1$ gäller för alla positiva heltal $n\ .$

Albiki

Hej!

Det gäller att visa sambandet

    $2 + 4 + 8 + 16 + \cdots + 2^{n-1} = 2^{n}\ .$

Albiki

Albiki skrev :

Hej!

Det är fel på nästan varje rad i bokens text! Vilken bok är det fråga om, så att jag ser till att undvika att den? Kan du skriva ner bokens ISBN-nummer?

Uppgiften skulle istället ha varit denna: Bevisa med matematisk induktion att formeln $S_n = \sum_{i=1}^{n}2^{n-1} = 2^{n}-1$ gäller för alla positiva heltal $n\ .$

Albiki

Albiki...dä ä inte enkelt å göra rätt :-)

$S_n=\sum _{i=1}^n{2}^{\mathit{i}\mathbf{-}\mathbf{1}}$

 Jo, det är inget som fungerar i detta uppgift! 

@Albiki: ISBN 978 91 47 10928 9

@Affe Jkpg: vilket fin avatar :D

@Smutstvätt: there is no magic!

$$\begin{gathered} VL: \sum _{i=1}^1=\hspace{0.17em}{2}^{1-1}=1 \\ HL: 2*1-1 = 1 \end{gathered}$$

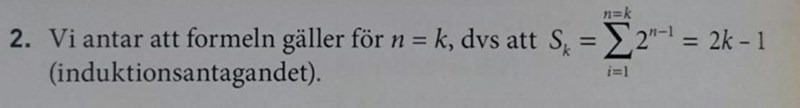
Det är OK...

$$\begin{gathered} VL: \sum _{i=1}^2=\hspace{0.17em}{2}^{2-1}+2^{1-1}=2+1 \\ HL: 2*2-1 = 3 \end{gathered}$$

Det är ok.

$$\begin{gathered} VL: \sum _{i=1}^3=\hspace{0.17em}{2}^{3-1}+ 2^{2-1}+2^{1-1}=4+2+1=7 \\ HL: 2*3-1 = 5 \end{gathered}$$

Det börjar lukta illa.

$$\begin{gathered} VL: \sum _{i=1}^4=\hspace{0.17em}{2}^{4-1}+ 2^{3-1}+2^{2-1}+2^{1-1}=8+4+2+1=15 \\ HL: 2*4-1 = 7 \end{gathered}$$

Nu luktar det definitivt surströmming.

Funkar dessa induktion bevis överhuvudtaket??

... det känns fel att inte försöka lösa den ändå...

Hej!

Steg 1. Sambandet är sant för $n=1$, eftersom $1 +1 = 2$.

Steg 2. Anta att sambandet är sant för heltalet $n-1$,

    $1+2+4+...+2^{n-2}=2^{n-1}.$

Steg 3. Visa att sambandet är sant för nästa heltal, $n$.

    $1+2+4+...+2^{n-2}+2^{n-1} = 2^{n-1}+2^{n-1} = 2^{1+(n-1)}=2^n.$

Steg 4. Enligt Induktionsaxiomet är sambandet sant för samtliga positiva heltal.

Oj det var snabbt!

Vart måste summa tecken skrivas?

$$\begin{gathered} 1+2+4+8+16....+2^{k-1})= \\ 1+2(1+2+4+8.+..+2^{k-2})= \\ 1+2(1+2(1+2+4+...+2^{k-3})= \\ 1+2(1+2(1+2(1+2+...+2^{k-4})= \\ 1+2(k-1)=2k-1 \end{gathered}$$

Tack Affe, 

jag har försökt vika ryska dockor på pappret, hur gör du den sista steg, från:

$1+2+(1+2(1+2(1+2(1+2^{6-5})$ om jag har nu inte slarvat 

till 

$1 +2(k-1)$ ?

Hur ''viker'' du alla 1 + 2?

Se figur

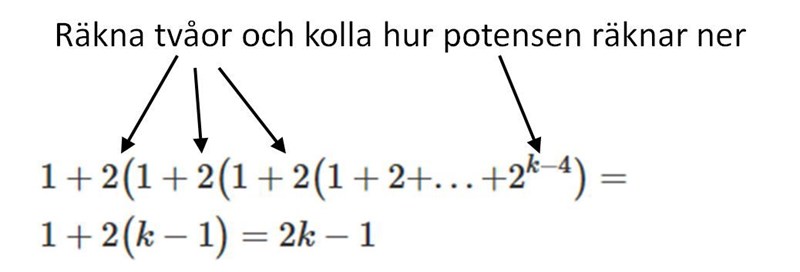
dajamanté skrev :

Tack Affe, 

jag har försökt vika ryska dockor på pappret, hur gör du den sista steg, från:

$1+2+(1+2(1+2(1+2(1+2^{6-5})$ om jag har nu inte slarvat 

till 

$1 +2(k-1)$ ?

Hur ''viker'' du alla 1 + 2?

Jo, du har slarvat med t.ex. det andra plus-tecknet.

Affe Jkpg skrev :

Se figur

Njo men, $2^{6-3}$ är inte lika som 2(6-3) liksom...?

Du har ju rätt Daja...jag har försökt bevisa något som är felaktigt!

För t.ex. n=6 gäller (jag vänder på ordningen för det kan vara mer pedagogiskt):
$$\begin{gathered} \sum _{i=6}^1{2}^{i-1}= \\ {2}^{6-1}+2^{5-1}+2^{4-1}+2^{3-1}+2^{2-1}+2^{1-1}= \\ {2}^{6-1}-1=63 \end{gathered}$$

Det är ju som ett binärt tal med sex "binärer" alla lika med ett:
11 1111
Så då får vi i stället:
$\sum _{i=1}^k{2}^{i-1}=2^k-1$

Åsså skäms jag, eftersom jag sysslar så mycket med denna typ av uppgifter :-)

Oroa dig inte för så lite, det är ingen som skäms mer på forumet än jag :)

Men nu måste jag fundera en ytterligare tag för att varför:

$2^{6-1}+2^{5-1}+2^{4-1}+2^{3-1}+2^{2-1}+2^{1-1}=2^6-1$

fungerar.

Varför $2^k-1$ är den högsta tal som man får när man har ''fullt'' på alla lägre binärer.

Och förresten kan man förkorta $2^5+2^4+2^3+2^2+2^1$, eftersom det är samma bas 2?

Ta och leta upp tråden om breven till Chirac och läs den igen - jag tror du kan känna igen ett mönster.

dajamanté skrev :

Oroa dig inte för så lite, det är ingen som skäms mer på forumet än jag :)

Men nu måste jag fundera en ytterligare tag för att varför:

$2^{6-1}+2^{5-1}+2^{4-1}+2^{3-1}+2^{2-1}+2^{1-1}=2^6-1$

fungerar.

Varför $2^k-1$ är den högsta tal som man får när man har ''fullt'' på alla lägre binärer.

Och förresten kan man förkorta $2^5+2^4+2^3+2^2+2^1$, eftersom det är samma bas 2?

Om du stött på hur man räknar med binära (basen 2) tal, så är t.ex. detta bekant:
100 0000 - 000 0001 = 011 1111

$2^6-2^0=2^5+2^4 + 2^3+2^2+2^1+2^0$

Jo, jag är tyyyyyp med conceptet att den högsta tal som man kan få med den binära system är att fylla på alla mindre lådorna, och det blir nästa ''låda'' minus ett.

Ska ha en ytterligare tittande på Chirac.