Induktion med olikhet

Hej, jag förstår mig på induktion allt bättre men tycker att det är rätt svårt att utföra induktionssteget när uppgiften är om en olikhet och ej om en sekvens summa.
Detta är frågan samt hur jag började lösa den, men vet inte hur jag ska komma vidare. Kan någon hjälpa mig med detta?

EDIT1: Svaret kvarstår, men ser nu att jag missade fakuliteten på (1+1) i basfallet.
EDIT2: Bild på den lösta uppgiften efter hjälp i chatten. Har jag gjort rätt?
Svaret ska ...<... och inte ...=... såklart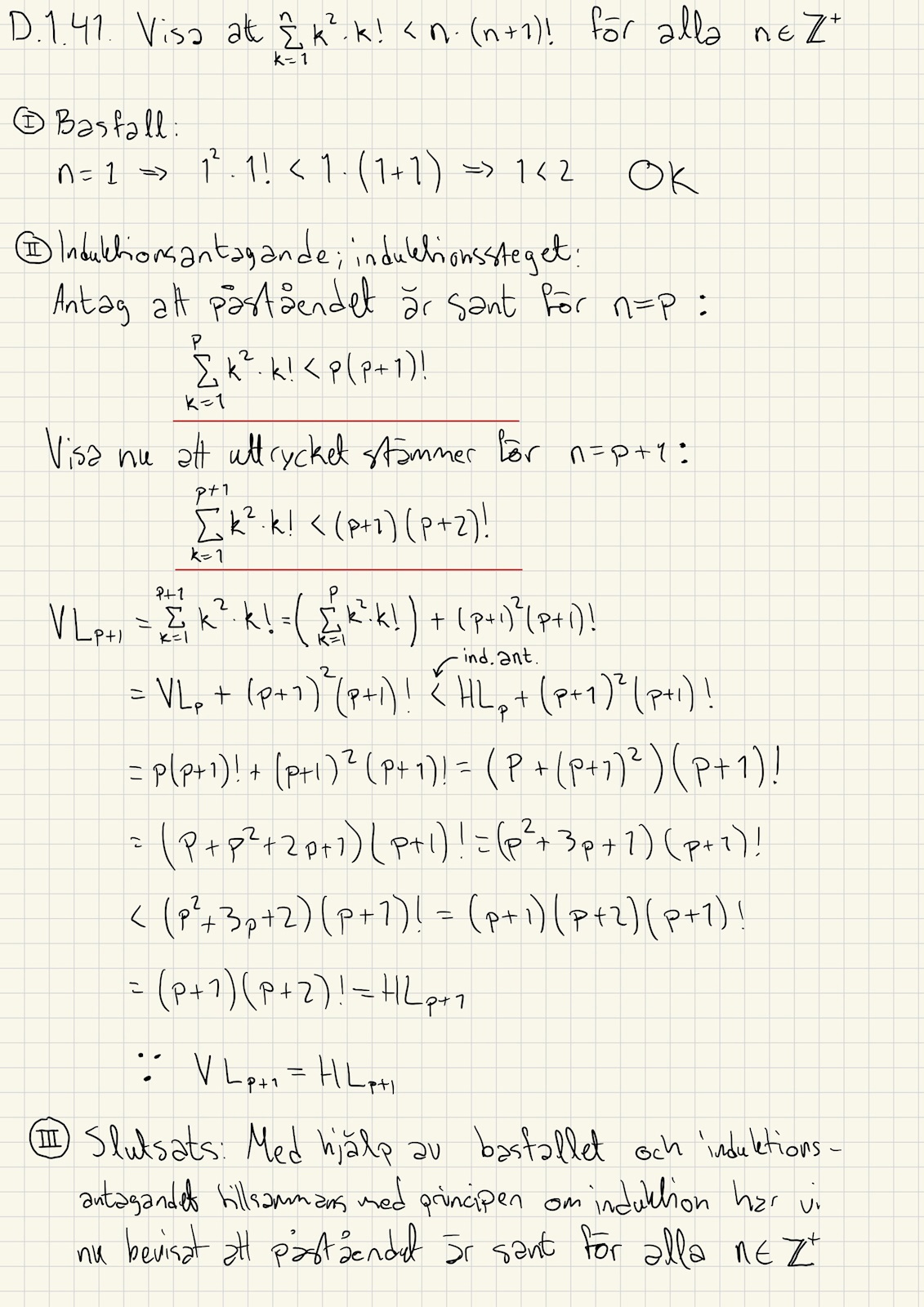

På samma sätt som du skrev om VL_p+1 på en form som var VL_p + [lite till], försök skriva om HL_p+1 på en form som är HL_p + [lite till].

Kan du bevisa att [lite till]-termen i högerledet är större än i vänsterledet så har du bevisat det.

EDIT: Alternativt kan du uttryckligen ta ditt sista uttryck ovan och ersätta HL_p med det som HL_p är, och se om det tillsammans med (p+1)(p+1)(p+1)! blir mindre än HL_p+1.

Bedinsis skrev:
...HL_p + [lite till]...

Blir det inte då att [lite till]-termen kommer att vara samma för $V L_{p}$ som för $H L_{p}$ , då HL alltid är summan av VL. Eller förstår du vad jag menar?

$V L_{p + 1} > H L_{p + 1} \Leftrightarrow V L_{p} + [l i t e t i l l] > H L_{p} + [l i t e t i l l]$

där lite till kommer att vara samma tal
EDIT: Det jag skrivit nu blir ju en likhet, inte en olikhet inser jag nu...

[lite till]-termen måste definitivt inte vara identisk i de två leden. Så länge vi kan bevisa att a<b och att c<d så måste a+c<b+d.

Det är också högst inkorrekt matematiskt språkbruk, som jag får be om ursäkt för att jag introducerade.

Bedinsis skrev:
EDIT: Alternativt kan du uttryckligen ta ditt sista uttryck ovan och ersätta HL_p med det som HL_p är, och se om det tillsammans med (p+1)(p+1)(p+1)! blir mindre än HL_p+1.

Jaja så att jag vet att

$H L_{p} + {(p + 1)}^{2} \times (p + 2)! < H L_{p + 1}$
så vet vi att induktionsantagandet stämmer

$V L_{p} + {(p + 1)}^{2} \times (p + 1)! \overset{i n d . a n t .}{<} H L_{p} + {(p + 1)}^{2} \times (p + 2)!$

då HL alltid kommer att vara en större del än VL. Är det så du menade?
Hela ledet skulle alltså bli följande:
$V L_{p + 1} = V L_{p} + {(p + 1)}^{2} \times (p + 1)! \overset{i n d . a n t .}{<} H L_{p} + {(p + 1)}^{2} \times (p + 2)! = p (p + 1)! + {(p + 1)}^{2} \times (p + 2)! < (p + 1) \times (p + 2)! = H L_{p + 1}$
Haha och fattar att det inte är så matematiskt, håller mig undan från det på tentor :P

Nej, det var inte så jag menade. Det jag menade var:

$H L_{p} + {(p + 1)}^{2} (p + 1)! = p (p + 1)! + {(p + 1)}^{2} (p + 1)! = (p + {(p + 1)}^{2}) (p + 1)!$

Och sedan se om (p+(p+1)²) på något sätt kan bevisas ge ett värde mindre än (p+1)(p+2), dvs. det man multiplicerar (p+1)! med för att få HL_p+1. Jag vet dock inte om detta funkar.

Jag tror du tappade bort en (p+1)!-faktor där ovan... och nu ser jag att du redigerar på ett sätt att jag tappar bort mig. Får återkomma.

Jag tog hjälp av din ansats har ev löst det. Om du orkar får du gärna ta en titt på lösningen!
$V L_{p + 1} = V L_{p} + {(p + 1)}^{2} \times (p + 1)! \overset{i n d . a n t}{<} H L_{p} + {(p + 1)}^{2} \times (p + 1)! = = p (p + 1)! + {(p + 1)}^{2} \times (p + 1)! = (p + {(p + 1)}^{2}) \times (p + 1)! = = (p^{2} + 3 p + 1) \times (p + 1)! < (p^{2} + 3 p + 2) \times (p + 1)! = = (p + 1) \times (p + 2) \times (p + 1)! = (p + 1) \times (p + 2)! = H L_{p + 1} ∴ V L_{p + 1} < H L_{p + 1}$

EDIT: Nu är ekvationen klar

Tjusigt. Jag skulle säga att det där är ett fullgott bevis, bra jobbat.

Oki great. Tack för hjälpen! :D

Svara

Visa senaste svar