Induktionsbevis - Fibonacci

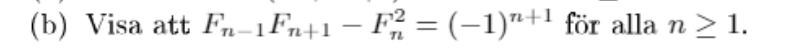
Hej,

Behöver hjälp med att bevisa ovanstående:

Vi prövar först med basfallet n = 1. I VL fås då:

$F_{0} F_{2} - {F_{1}}^{2} = 1 (2) - 1^{2} = 1$

I HL fås (-1)^2 = 1. Därav är VL och HL densamma.

Nu antar vi att påstående stämmer för alla n >= 1, och prövar för n = p, där p tillhör de naturliga positiva heltalen.

$F_{p} F_{p + 2} - {F_{p + 1}}^{2}$

Jag har sedan efter detta försökt göra några substitutioner med hjälp av definitionen av Fibonnacis talföljd, men det verkar inte komma någonstans. Har ni något tips på vad jag kan börja med åtminstone?

Tack!

Om du skall göra ett induktionsbevis, så skall du göra ett induktionsantagande, nämligen att F_p-1F_p+1-F_p² = (-1)^p+1 och försöka bevisa att i så fall så är F_pF_p+1-F_p+1² = (-1)^p+2. Börja med vänsterledet och försök få fram HL. Använd dig av induktionsantagandet.

Smaragdalena skrev:
Om du skall göra ett induktionsbevis, så skall du göra ett induktionsantagande, nämligen att F_p-1F_p+1-F_p² = (-1)^p+1 och försöka bevisa att i så fall så är F_pF_p+1-F_p+1² = (-1)^p+2. Börja med vänsterledet och försök få fram HL. Använd dig av induktionsantagandet.

Det blir väl $F_pF_{p+2}...$ ?

Du har rätt, jag skrev fel.

Svara Avbryt

Visa senaste svar