Induktionsprincip över heltalslistor
Hej!
Jag vet inte om det här är mer matematik eller mer datalogi, eller egentligen är det en mix av båda, så hoppas att jag valt rätt kategori.
Jag förstår inte riktigt Övning 3.1. Innan jag tar min fråga så kommer här relevanta definitioner + själva Övning 3.1:
Poängen är med en sån här notation kan man visa att funktioner som man definierat på listor är sanna.
I notationen är exempelvis listan 1, 2, 3: cons(1, cons(2, cons(3, empty))).
Hursomhelst, det jag inte fattar är varför induktionsprincipen kvantifierar över alla P på det här sättet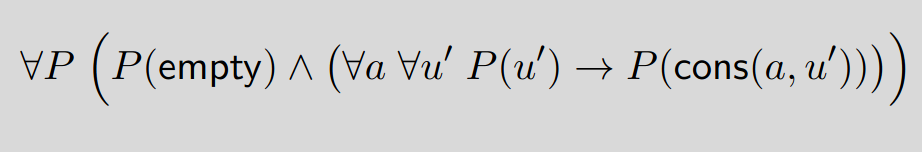
Jag vet att uppgiften ber att "kvantifiera över alla predikat P", men eftersom högerledet av den yttre implikationen verkar avse ett specifikt P, så borde väl parenteserna ändå se ut så här?
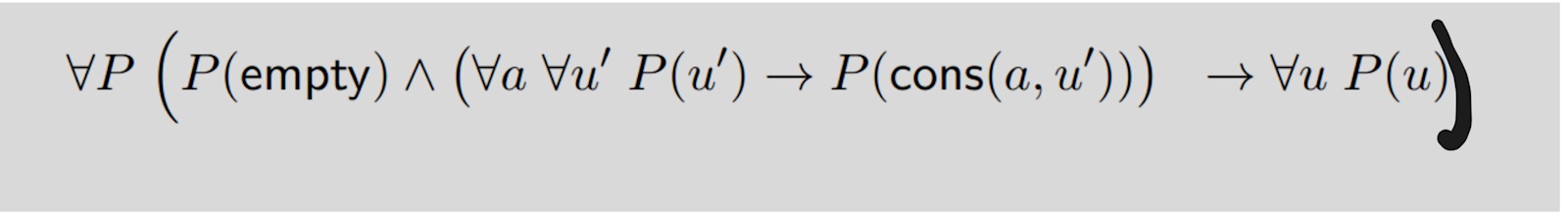
En annan uppgift senare i häftet har gjort samma sak (kvantifierat längs med alla P på vänsterledet av den yttre implikationen, inte runt hela), vilket gör så att jag börjar misstänka att det är jag som har fel.
De kanske vill ha sagt att om det gäller för alla P så gäller det för något visst P som de tänker på, men det är i så fall olämpligt att använda samma variabelnamn för båda. Jag tycker som du.
Laguna skrev:De kanske vill ha sagt att om det gäller för alla P så gäller det för något visst P som de tänker på, men det är i så fall olämpligt att använda samma variabelnamn för båda. Jag tycker som du.
Tack för svar!
