Injektivitet rotation i planet

Om v är skild från u gäller det då att F(v) är skild från F(u)? Du kan tänka olika fall: u och v har olika riktning; u och v har samma riktning men olika belopp.

PATENTERAMERA skrev:

Om v är skild från u gäller det då att F(v) är skild från F(u)? Du kan tänka olika fall: u och v har olika riktning; u och v har samma riktning men olika belopp.

Menar du att om e1 är skild från e2 så gäller det att F(e1) är skild från F(e2)? Jag tror jag blir förvirrad över den geometriska tolkningen som jag använt för de andra uppgifterna t.ex. att den är injektiv då Y=AX har högst en lösning X eller att om AX1=AX2 så ska x1=x2. 

Hur menar du att dela upp det i fall? Skrev såhär nu. 

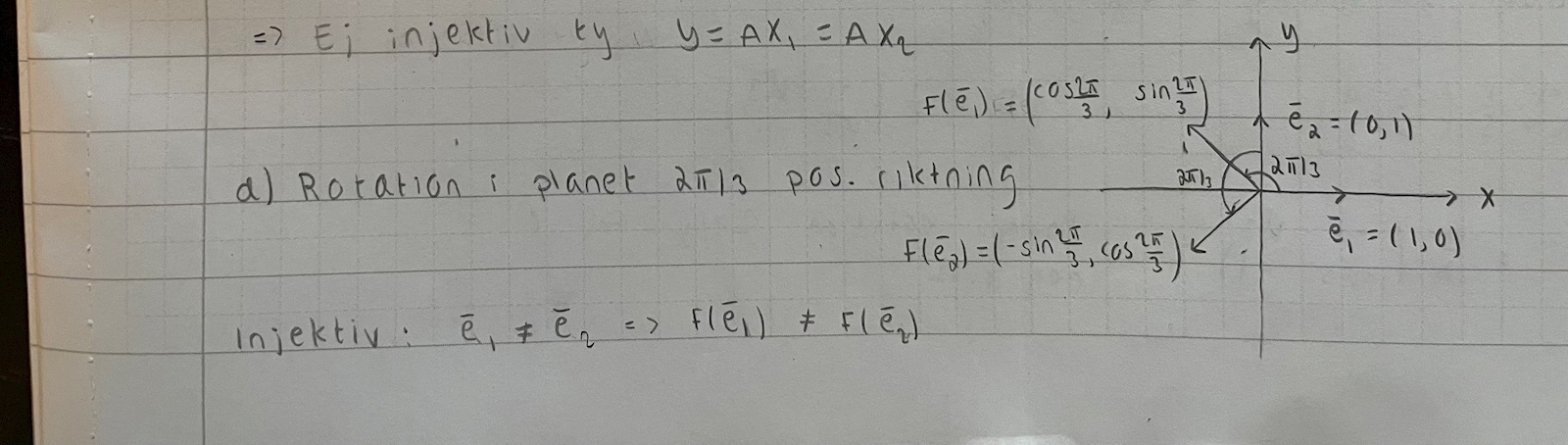
F(u) = F(v) => u = v är ekvivalent med att u $\ne$ v => F(u) $\ne$ F(v). Så det är ekvivalenta test.

Notera att detta skall gälla för alla möjliga vektorer u och v. Så det är inte tillräckligt att bara konstatera att detta gäller för två vektorer. Dock om du kan visa att F avbildar en bas på en bas så är avbildningen injektiv (och surjektiv). Dvs om F(e1) och F(e2) utgör en bas för R² så är avbildningen injektiv.

Jag tänkte så här. Om u och v har olika riktning så är vinkeln mellan dem skild från noll. Kalla denna vinkel a. Om jag roterar både u och v 2pi/3 radianer så kommer vinkeln mellan dem efter rotation fortfarande vara a - geometriskt uppenbart - och de roterade vektorerna är därför olika. Ett liknande resonemang kan göras då vektorerna har samma riktning men olika belopp eftersom en rotation inte påverkar en vektors längd.

Ytterligare ett sätt är att visa att det finns en vänsterinvers G till rotationen F (en funktion är injektiv om och endast om den har en vänsterinvers). Här är det enkelt att inse att om vi väljer G till rotation med -2pi/3 radianer så måste det gälla att G(F(v)) = v, eftersom om vi först roterar med 2pi/3 och sedan med -2pi/3 så får vi tillbaka den vektor som vi startade med. Så G är en vänsterinvers (och en högerinvers), och F är därför injektiv.