1
svar
126
visningar
Instängning av summa
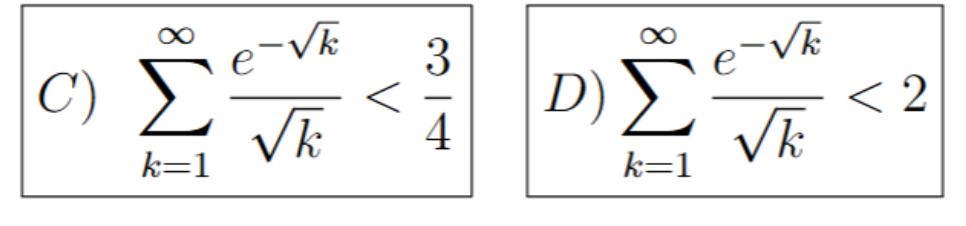
Behöver hjälp med att avgöra vilket av alternativen som är korrekt.
Det är ju ingen geometrisk serie så det enda sättet att kvantifiera summan måste vara via instängning (antar jag)
Man kan ju jämföra summan med en integral.
Funktionen är avtagande för .
Den givna summan kan skrivas som . Den är en undersumma till och en översumma till , d.v.s. det gäller att

