Intagningsprov hvitfeldtska 2010 uppgift 4

Hej, jag har tänkt att gå på hvitfeldtskas matematiskspets natur, och därför kollade jag runt på gamla intagningsprov.

I provet från 2010 hittade jag en uppgift som lyder såhär:

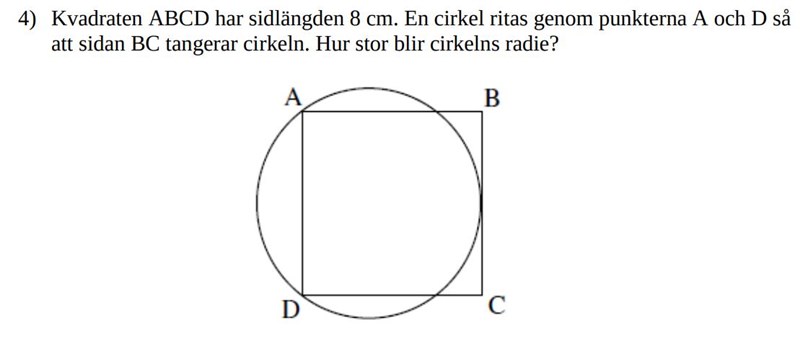
Jag kan inte lösa uppgiften hur jag än tänker.

Jag har försökt att göra något med kvadratens diameter, eller att göra en triangel i kvadraten, och min lärare visste inte heller vad man skulle kunna göra mer.

Jag är extremt tacksam för svar, eftersom det inte finns facit till dessa intagningsprov.

Tack på föprhand!

Var hamnar cirkelns mittpunkt? Tänk på att cirkelns mittpunkt har lika långt till alla punkter på cirkeln.

Om du tänker på att AD är en korda och att du kan dra en korda ortogonalt mot AD genom cirkelns mittpunkt.

$K v a d r a t e n s s i d o r : 2 y = x + 1 \Rightarrow x = 2 y - 1$

$P u t h a g o r a s g e r : 0 = {(2 y - 1)}^{2} + y^{2} - 1 \Rightarrow y \Rightarrow x$

När du tagit reda på triangelns sidor kan du skala upp kateterna med 4:a och lösa ut radien/ hypotenusan. Svaret blir då att radien=5

Ett alternativ är att rita ut dra följande sträckor i figuren och sedan tillämpa Pythagoras sats i den rätvinkliga triangel som uppstår.

1PLUS2 skrev:
$K v a d r a t e n s s i d o r : 2 y = x + 1 \Rightarrow x = 2 y - 1$
$P u t h a g o r a s g e r : 0 = {(2 y - 1)}^{2} + y^{2} - 1 \Rightarrow y \Rightarrow x$
När du tagit reda på triangelns sidor kan du skala upp kateterna med 4:a och lösa ut radien/ hypotenusan. Svaret blir då att radien=5

Skulle du kanske kunna förklara lite mer på vad du gjorde vid "Pythagoras ger"? Jag har suttit och tänkt, men jag fattar inte riktigt...

Du har en rätvinklig triangel där de båda korta sidorna är y respektive 2y-1 och där den långa sidan är 1. Kan du sätta upp Pythagoras sats för denna triangel och lösa den? Om du behöver mer hjälp, så visa hur långt du har kommit pch fråga igen.

Smaragdalena skrev:
Du har en rätvinklig triangel där de båda korta sidorna är y respektive 2y-1 och där den långa sidan är 1. Kan du sätta upp Pythagoras sats för denna triangel och lösa den? Om du behöver mer hjälp, så visa hur långt du har kommit pch fråga igen.

Vad kommer 1:an ifrån?

nikoniko skrev:
Smaragdalena skrev:
Du har en rätvinklig triangel där de båda korta sidorna är y respektive 2y-1 och där den långa sidan är 1. Kan du sätta upp Pythagoras sats för denna triangel och lösa den? Om du behöver mer hjälp, så visa hur långt du har kommit pch fråga igen.
Vad kommer 1:an ifrån?

Det är en bra fråga. Ettan står ju som markering för radien, som är okänd. Bättre att sätta ett $r$ där!

Skaft skrev:
nikoniko skrev:
Smaragdalena skrev:
Du har en rätvinklig triangel där de båda korta sidorna är y respektive 2y-1 och där den långa sidan är 1. Kan du sätta upp Pythagoras sats för denna triangel och lösa den? Om du behöver mer hjälp, så visa hur långt du har kommit pch fråga igen.
Vad kommer 1:an ifrån?
Det är en bra fråga. Ettan står ju som markering för radien, som är okänd. Bättre att sätta ett $r$ där!

Ok, tack, det fattar jag. Men jag fattar ändå inte riktigt det andra...

Jag tycker AlvinB's approach och bild är lättare att följa:

AlvinB skrev:
Ett alternativ är att rita ut dra följande sträckor i figuren och sedan tillämpa Pythagoras sats i den rätvinkliga triangel som uppstår.

Hur blir det om du ställer upp Pythagoras sats för den triangeln?

Skaft skrev:
Jag tycker AlvinB's approach och bild är lättare att följa:
AlvinB skrev:
Ett alternativ är att rita ut dra följande sträckor i figuren och sedan tillämpa Pythagoras sats i den rätvinkliga triangel som uppstår.
Hur blir det om du ställer upp Pythagoras sats för den triangeln?

Då blir det :

4^2+(8-r)^2=r^2

16+64−16r+r^2=r^2

80-16r+r^2=r^2

80-16r=0

80=16r

5=r

radien = 5

Herregud, jag fattar! Tack så hemskt mycket för hjälpen!

Svara

Visa senaste svar