Integral (1+x)/(1-x)dx

Jag tänker att variabelsubstitution vore bra här! Kanske $t=1-x$ skulle kunna fungera? :)

Utför divisionen så får du en kvot och rest. 

$$\begin{gathered} Long division \\ \frac{1+x}{1-x}=-x-1/x-1=-1 och 2 i rest \end{gathered}$$

De här brukar gå enklare att bara plussa på det man vill ha och minusa lika mycket tycker jag.

Och det är otrevligt att ha x negativt i nämnaren i onödan, det leder nästan alltid till en bortglömd inre derivata.

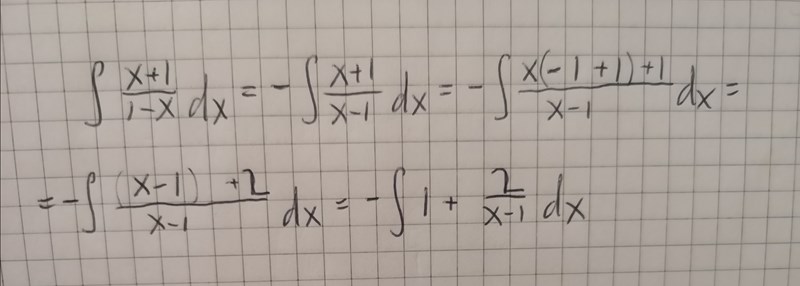
Jag förstår principen du gör här, men kan man alltså ändra tecken bara i nämnaren och sätta - framför integralen. Trodde täljaren förändrades till -x-1 då ocskå?

Liddas skrev:

Jag förstår principen du gör här, men kan man alltså ändra tecken bara i nämnaren och sätta - framför integralen. Trodde täljaren förändrades till -x-1 då ocskå?

Du kan antingen sätta "det andra minustecknet" utanför integraltecknet eller framför hela täljaren, det går på ett ut. 

Ja tack jag kom på det.

Tack för era svar, din lösning macimacko var väldigt straight forward!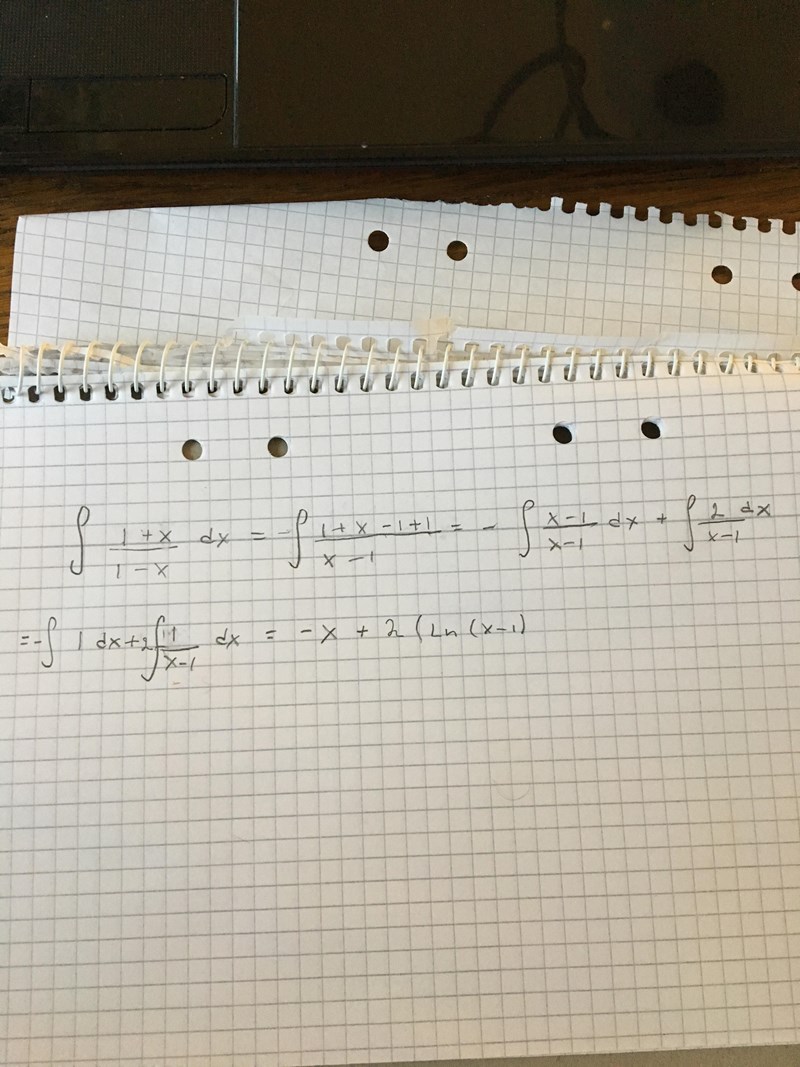

Hej,

Micimacko misstog sig litet grand då hon skrev att $-\frac{x+1}{x-1}$ är samma sak som $-\frac{x(-1+1)+1}{x-1}$ eftersom $-1+1 = 0$ så då står det att $-\frac{x+1}{x-1} = -\frac{0+1}{x-1} = -\frac{1}{x-1}$.

Idén är att utnyttja att täljare och nämnare liknar varandra.

• Skriv täljaren som $x+1 = 2-(1-x)$ och dividera sedan med nämnaren för att få en integral som är lättare att bestämma.

    $\displaystyle\int \frac{x+1}{1-x}\,dx = \int \frac{2-\left(1-x\right)}{1-x}\,dx = \int \frac{2}{1-x}-1\,dx= -2\ln\left|1-x\right|-x+C.$