Integral

Är dettta ett bra sätt att lösa denna uppgift på? försökte hitta video på hur man skulle kunna göra det här och i vilka fall man vet när man behöver göra det. Men har inte hittat något
M (a) * x skrev:
Är dettta ett bra sätt att lösa denna uppgift på? försökte hitta video på hur man skulle kunna göra det här och i vilka fall man vet när man behöver göra det. Men har inte hittat något
Jag tror Månsson kallar denna ”övertäckningsmetoden”
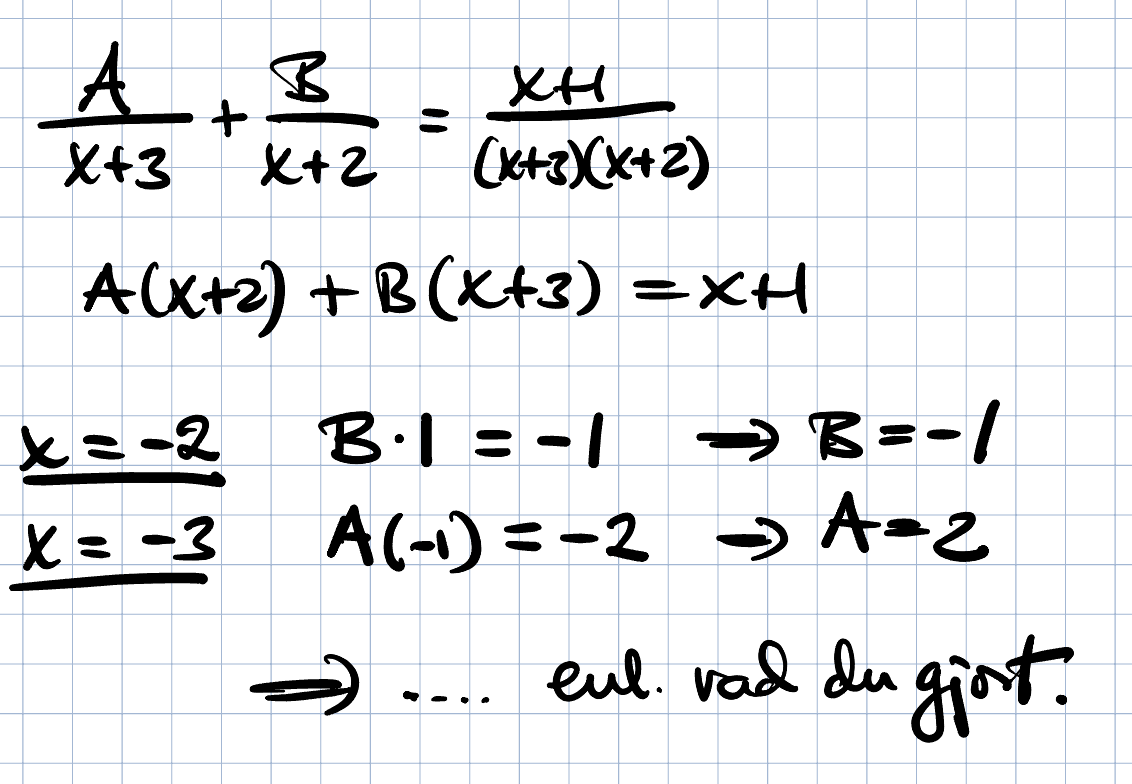
Kolla in hans YouTube-kanal så kanske han visar den mera i detalj där.
Ibland kallas det handpåläggning, se länken
Det ser ut som om man delar med 0, men om man tänker sig att man multiplicerar med alla nämnarna först så går det att förstå.
Laguna skrev:Det ser ut som om man delar med 0, men om man tänker sig att man multiplicerar med alla nämnarna först så går det att förstå.
Ja, det är lite regelvidrigt, ty man borde skriva vid första raden x=/={-3,-2}... och sedan använder man just det. "Koefficientbalansering" är troligen det mest logiska, men kräver mera beräkningar.
Det är ingen mystik inblandad i detta. A och B ska bestämmas så att likheten A(x+2)+B(x+3)=(x+3) ska gälla för alla x. Speciellt ska den då gälla för x=-2 resp. x=-3.
Tomten skrev:Det är ingen mystik inblandad i detta. A och B ska bestämmas så att likheten A(x+2)+B(x+3)=(x+3) ska gälla för alla x. Speciellt ska den då gälla för x=-2 resp. x=-3.
Du kan inte en sekunden skriva att x=/={-3,-2} för
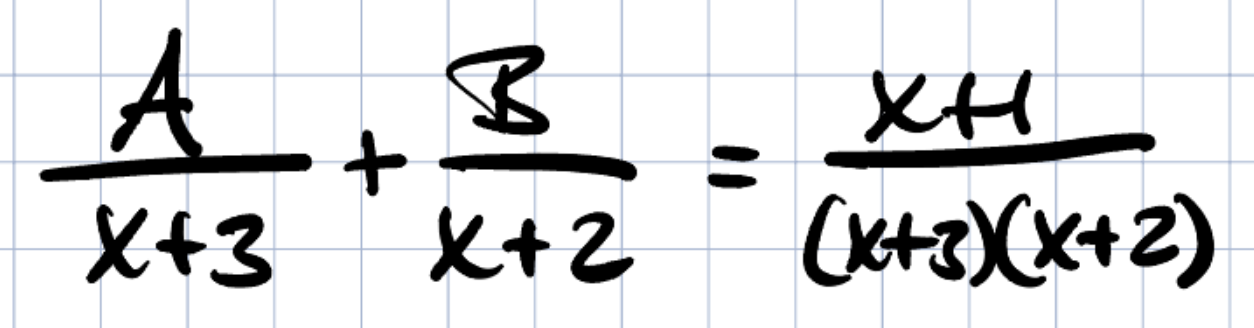
för att sedan låta x vara just dessa tal. Det är som att säga att
f(x)=1/x, x=/=0
och sedan när man ritar kurva börja undra varför det inte funkar så bra för x=0.
Här råkar det dock bli enkla räkningar om man gör så, men det finns ingen logik i det givet definitionsområdet.
Det var inte den raden mitt inlägg handlade om utan raden A(x+2)+B(x+3)=x+1 Och den raden var en följd av: Antag att det finns konstanter A och B sådana att A/(x+3)+B/(x+2)=(x+1)/(x+2)(x+3).
Notera också att integrationsintervallet är [0,1] och där har integranden inga singulariteter.



