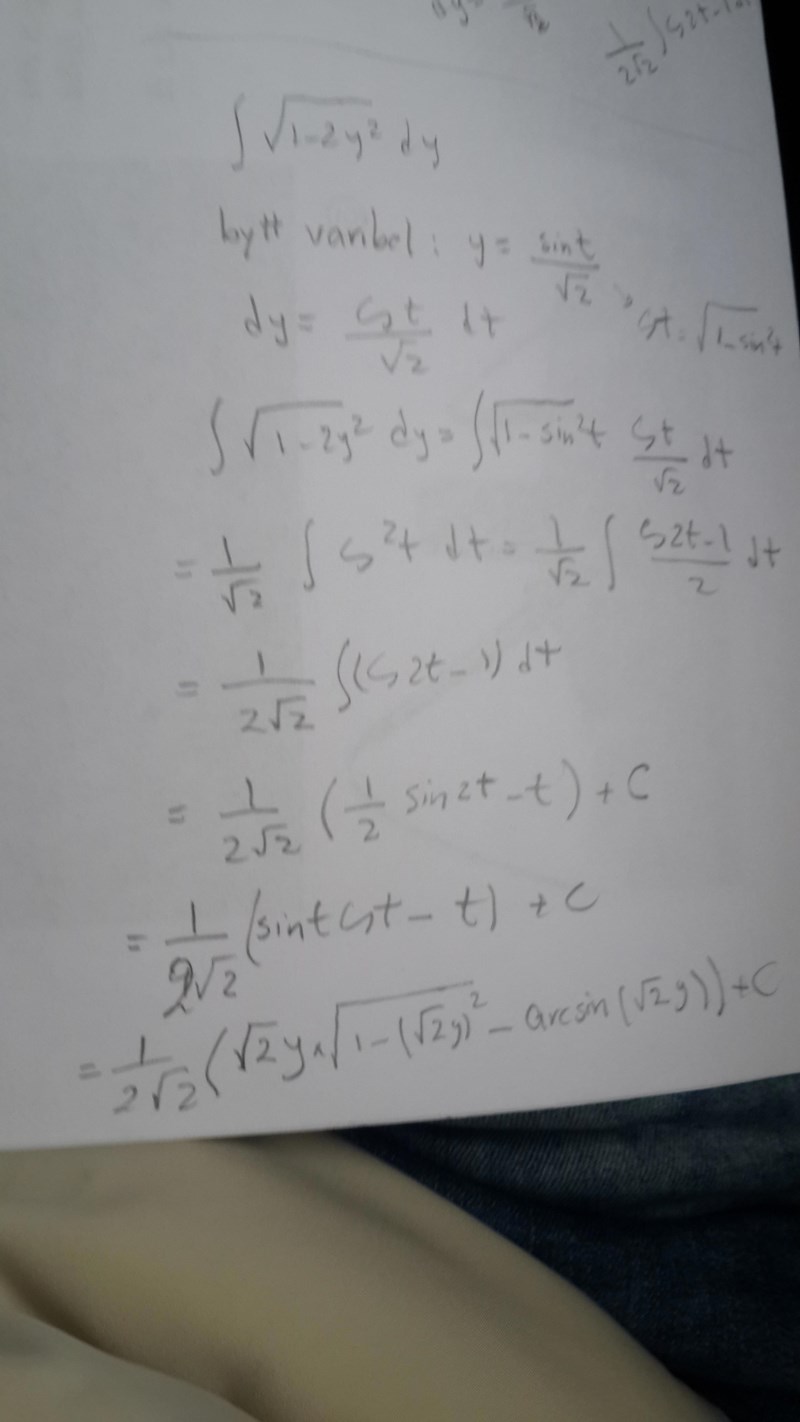Integral flervariabel
Hej,
Jag har det lite kämpigt med två integraler.. Jag kan se att det går att lösa uppgiften med hjälp av dessa två integraler när jag kollar med miniräknare men sen kan det ju hända att jag ställt upp uppgiften mindre fördelaktigt från början. Hur som helst.
Någon som har tips på hur man kan lösa:
Integral( sqrt(1-2*y^2)) m.a.p. y .. samt
Integral( y^2 * sqrt(1-2*y^2)) m.a.p. y
Där sqrt = roten ur
Tack på förhand,
Mvh Andreas
Ser ut att stämma bra med vad räknaren föreslår. Jag ska kolla lite noggrannare på metodiken imorgon. Tack för ledning!
Hej!
Med en partiell integration kan man skriva integralen
.
Sedan är
så att integralen kan skrivas
.
Du ser att
.
Sedan är det ett standardresultat att integralen
Albiki