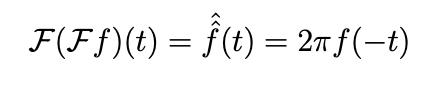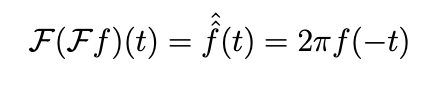Integral med Parsevals formel

Din första transform verkar ha vänt på tecknet? Använd istället

$\displaystyle \hat{f}(\omega)=\pi\left(\theta(\omega+1)-\theta(\omega-1)\right)$

Sen är jag inte riktigt med på vad som händer i slutet, använd istället egenskapen hos den generaliserade deltafunktionen för att plocka ut funktionsvärdet för en given punkt

$\displaystyle \int_{-\infty}^\infty h(\omega)\delta(\omega-c)\,d\omega=h(c)$

Eller att $(\theta(\omega+1)-\theta(\omega-1))$ är $1$ i intervallet $-1<><>$, annars 0.

I det sista fallet får du kvar integralen

$\displaystyle \frac{\pi}{2} \int_{-1}^1\left(\delta(\omega+a)+\delta(\omega-a)\right)\,d\omega$

Nu får du utnyttja den något mer aggressiva varianten av att plocka ut ett funktionsvärde:

$\displaystyle \int_{c-\epsilon}^{c+\epsilon}h(\omega)\delta(\omega-c)=h(c)$

För något $\epsilon>0$ (Sifting property)

D4NIEL skrev:

Din första transform verkar ha vänt på tecknet? Använd istället

$\displaystyle \hat{f}(\omega)=\pi\left(\theta(\omega+1)-\theta(\omega-1)\right)$

Sen är jag inte riktigt med på vad som händer i slutet, använd istället egenskapen hos den generaliserade deltafunktionen för att plocka ut funktionsvärdet för en given punkt

$\displaystyle \int_{-\infty}^\infty h(\omega)\delta(\omega-c)\,d\omega=h(c)$

Eller att $(\theta(\omega+1)-\theta(\omega-1))$ är $1$ i intervallet $-1<><>$, annars 0.

I det sista fallet får du kvar integralen

$\displaystyle \frac{\pi}{2} \int_{-1}^1\left(\delta(\omega+a)+\delta(\omega-a)\right)\,d\omega$

Nu får du utnyttja den något mer aggressiva varianten av att plocka ut ett funktionsvärde:

$\displaystyle \int_{c-\epsilon}^{c+\epsilon}h(\omega)\delta(\omega-c)=h(c)$

För något $\epsilon>0$ (Sifting property)

Tack för svar!

På Fouriertransformen av f(t) tänkte jag följande:

Den inversa Fouriertransformen av $2\frac{sin(w)}{w} = \theta(t+1)-\theta(t-1)$

Men eftersom jag ska Fouriertransformera $\frac{sin(t)}{t}$ igen använde jag "kjedjeregeln"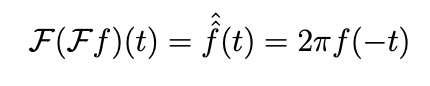

Alltså borde jag bara kunna förlänga med 2/2 på $\frac{sin(t)}{t}$ och multiplicera 2$\pi$ (och sedan förkorta bort 2) med $\theta(t+1)-\theta(t-1)$ och sätta in -t i funktionen, vilket blir varför det blir omvänt tecken. 

Sedan tänker jag att jag gör som du förklarar? Först byter jag gränserna eftersom theta funktionen endast är 1 i intervallet $-1 < w=""><>$, och sen att delta funktionen endast har "positiv massa" i a och -a, vilket kommer ligga utanför integrationsgränserna om $|a| > 1$, och om $|a|<>$ kommer integralen passera båda deltafunktionerna vilket leder till 1+1. 

artistfromspace23 skrev:

 

På Fouriertransformen av f(t) tänkte jag följande:

Den inversa Fouriertransformen av $2\frac{sin(w)}{w} = \theta(t+1)-\theta(t-1)$

Men eftersom jag ska Fouriertransformera $\frac{sin(t)}{t}$ igen använde jag "kjedjeregeln"

Alltså borde jag bara kunna förlänga med 2/2 på $\frac{sin(t)}{t}$ och multiplicera 2$\pi$ (och sedan förkorta bort 2) med $\theta(t+1)-\theta(t-1)$ och sätta in -t i funktionen, vilket blir varför det blir omvänt tecken. 

Ja, så kan man göra, men då blir summan av stegfunktionerna:

$\theta(1-\omega)-\theta(-\omega-1)=\theta(\omega+1)-\theta(\omega-1)$

Som ser ut så här:

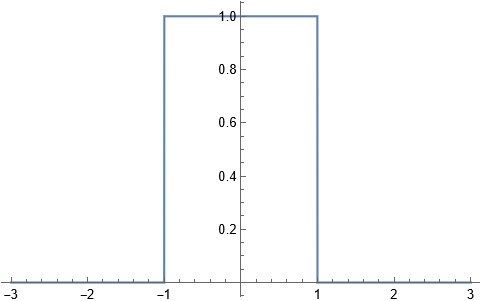
Din föreslagna stegfunktion $\theta(\omega-1)-\theta(\omega+1)$ ser ut så här

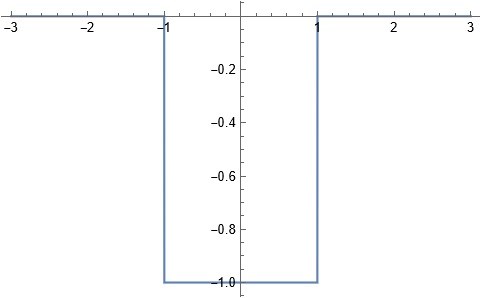Vilket felaktigt leder till -$\pi$ när $|a|<>$. Därför är det oroväckande att du ändå får rätt svar. Är du med? Förövrigt ganska säker på att $\displaystyle \frac{\sin(at)}{\pi t}$ finns med i Betas tabell över Fouriertransformer.

D4NIEL skrev:

artistfromspace23 skrev:

 

På Fouriertransformen av f(t) tänkte jag följande:

Den inversa Fouriertransformen av $2\frac{sin(w)}{w} = \theta(t+1)-\theta(t-1)$

Men eftersom jag ska Fouriertransformera $\frac{sin(t)}{t}$ igen använde jag "kjedjeregeln"

Alltså borde jag bara kunna förlänga med 2/2 på $\frac{sin(t)}{t}$ och multiplicera 2$\pi$ (och sedan förkorta bort 2) med $\theta(t+1)-\theta(t-1)$ och sätta in -t i funktionen, vilket blir varför det blir omvänt tecken. 

Ja, så kan man göra, men då blir summan av stegfunktionerna:

$\theta(1-\omega)-\theta(-\omega-1)=\theta(\omega+1)-\theta(\omega-1)$

Som ser ut så här:

Din föreslagna stegfunktion $\theta(\omega-1)-\theta(\omega+1)$ ser ut så här

Vilket felaktigt leder till -$\pi$ när $|a|<>$. Därför är det oroväckande att du ändå får rätt svar. Är du med? Förövrigt ganska säker på att $\displaystyle \frac{\sin(at)}{\pi t}$ finns med i Betas tabell över Fouriertransformer.

Ja... tack för förklaring. Givetvis borde det vara så. Det är nog jag som har stirrat mig blind på det korta lösningsförslaget. Med mitt svar på stegfunktionen blir integrationsgränserna omvända, och därför om man bryter ut ett minustecken från integralen så gränserna blir korrekt blir svaret -$\pi$, förstår jag det korrekt?

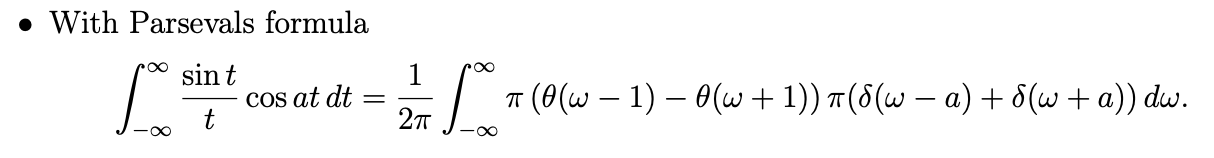
Får tyvärr endast använda tabellen som ges på tentamen, så vill inte använda något annat nu när jag studerar inför den