integral mellan en area

svaren ska vara tvärtom ordning så egentligen är svaret på a, b istället och svaret på b,a istället

a och b är integrationsgränser. Dessa begränsas bara av vart funktionen innanför integraltecknet är definierad. Det går till exempel att tänka sig att b antar sitt minsta värde, som är a. Om man väljer a så stort minus det går, vad kan man då välja b som om b måste vara större än a.

jag satte in x^2-1=0 och fick x=1 och X=-1 skulle det fungera som integrationsgränser

den minsta är -1 och den största är 1

Frågan gäller att bestämma a och b så att integralen har sitt minimum.  Du ska alltså svara med vad a ska vara och vad b ska vara.

Det är en bra början att hitta skärningarna med x-axeln. Vad blir integralen om du väljer skärningarna som a och b? Kan du välja andra a och b för att få ett mindre värde?

Jag fattar men hur finner man andra a och b? Det var förstås ett svar jag fick när jag satte in x^2-1=0 för att bestämma a och b. I och med det kommer jag inte riktigt på en annan lösning. (Notera: Jag är lite dålig på att förstå kopplingen), jag tänkte annars kanske göra upp a och b som en integral för att hitta minimum punkten kanske är det fel tankesätt.

Sätt in lite olika värden på a och b. Försök se vad som händer med integralen när du varierar a och b. Integrationsgränserna får du välja hur du vill om det inte står något speciellt i texten. Integralen ger arean under grafen från punkten x_1 = a till punkten x_2 = b.

a) är väl korrekt löst, tycker jag.

Hej!

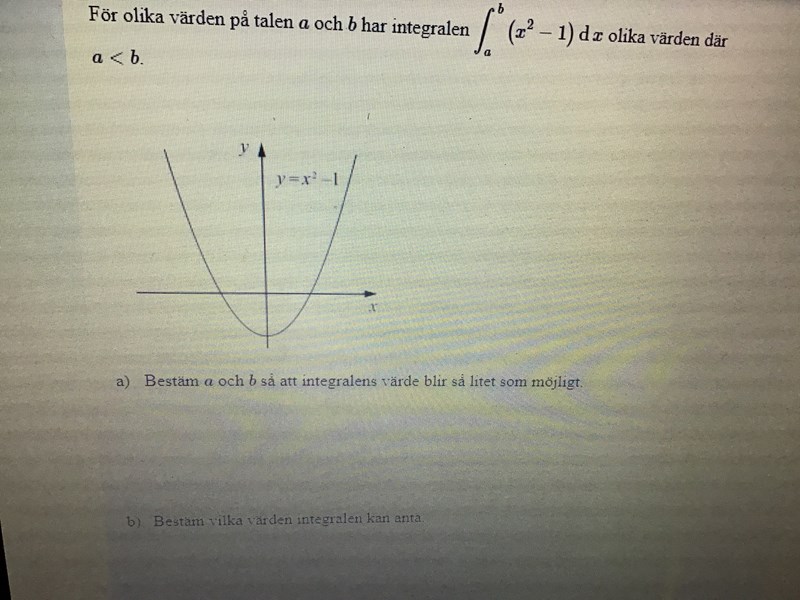
Integralen $\int_{a}^{b} f(x)\,dx$ ger arean (med tecken) som begränsas uppåt och nedåt av grafen till $f$ och $x$-axeln och som begränsas vänster och höger av linjerna $x=a$ och $x=b$.

Figuren visar att 

• Om $a<b<-1$ så är integralen positiv.
• Om $-1\leq a<b\leq1$ så är integralen negativ.
• Om $1<a<b$ så är integralen positiv.

Några speciella saker att notera är:

• Om $a=b$ så är integralen noll.
• Om man väljer $a<-1<b<1$ på lämpligt sätt så är det möjligt att få integralen noll.
• Om man väljer $-1<a<1<b$ på lämpligt  sätt är det möjligt att få integralen noll.
• Om man väljer $a<-1$ och $b>1$ på lämpligt sätt är det möjligt att få integralen noll.

Integralens minsta möjliga värde är ett negativ tal som alltså fås då man väljer $-1\leq a<b\leq1$ så att $a=-1$ och $b=1$; figuren visar att integralen blir mer negativ ju närmare $a$ är $-1$ och ju närmare $b$ är $1$.