integral över godtyckligt område
Hej
jag sitter med en uppgift där man ska lösa en dubbelintegral över ett godtyckligt område:
Beräkna , där D är det begränsade området i den första kvadranten avgränsat av linjen 2x+2y=5 och hyperbeln xy=1
jag började med att rita upp integrationsområdet där D är det streckade området:
 Innan man kan gå vidare och beräkna måste man få fram gränsvärdena till integralerna och där skulle jag behöva lite hjälp.
Innan man kan gå vidare och beräkna måste man få fram gränsvärdena till integralerna och där skulle jag behöva lite hjälp.
Hur har du försökt och hur långt har du kommit?
Nej, det är inte integrationsområdet som är skuggat.
Om du skriver upp de båda sambanden får du ett ekvationssystem, och det i sin tur ger en andragradsekvation du kan lösa för att få fram skärningspunkterna mellan linjen 2x+2y = 5 och hyperbeln xy = 1.
jag får att x=1/2 och y=2, eller x=2 och y=1/2
så skärningspunkterna blir då (1/2,2) och (2,1/2)
får vi då
Det ser vettigt ut. Vet du hur du skall fortsätta?
jag får att och sedan integrerar jag 1dx och får tillslut får jag då
Jag tolkar det som att området du ska integrera funktionen över ser ut så här:
.jpg?width=800&upscale=false)
Jag tycker alltså att integrationsgränserna borde vara till , till .
okej jag hade precis satt:
för
men på ditt sätt får vi en integral mindre så det är nog bättre.
Kan vi då skriva integralen som
integrerar vi i x led får vi
Guggle har rätt, jag tänkte fel.
Till T.S. Varför skriver du att integrationsområdet (D) är godtyckligt? Det är ju fullständigt specificerat.
jag inser nu att det blev missvisande, frågan var helt enkelt under den rubriken i boken.
vad blir nästa steg efter att man då har räknat fram , jag har lite svårt att ta mig vidare med
Integrationsområdet är alltså
Prova att införa variabler och .
om vi utför variabelbytet så får vi då att linjen 2x+2y=5 blir 2u=5 och sedan hyperbeln v=1
och integrationsområdet blir då men jag förstår inte hur ska vi göra med x>0 och y>0 när vi går över till u och v? men både u och v kommer ju vara större än noll eftersom både x och y är positiva.
Idil M skrev:vad blir nästa steg efter att man då har räknat fram , jag har lite svårt att ta mig vidare med
Eftersom gränserna för y är beroende av x bör du behandla dem först (dvs i den inre integralen). Så här
.
Där vi utnyttjade följande från grundkursen minnet/integralkatalogen, eller härledde medelst partiell integration:
så vi bytte ordning från dxdy till dydx eftersom vi har 1/x och (5-2x)/2 som integrationsgränserna för y som därmed är beroende av x. Det vi har nu är alltså och nu ska vi beräkna
Nä, är värdet på hela dubbelintegralen.
I första steget integrerar vi i y-led och låtsas att alla x är konstanter. Den primitiva funktionen blir bara y och sätter vi in gränserna istället för y får vi kvar den yttre integralen:
okej, jag är inte helt med. Först sätter vi där alltså är gränserna vi har för y från den ursprungliga dubbelintegralen.
sedan tar vi fram den primitiva funktionen till och sätter in gränserna 2 och 1/2 som ju är gränserna för x?
Idil M skrev:okej, jag är inte helt med. Först sätter vi där alltså är gränserna vi har för y från den ursprungliga dubbelintegralen.
Just det. Integralen i y blir ju bara
sedan tar vi fram den primitiva funktionen till och sätter in gränserna 2 och 1/2 som ju är gränserna för x?
Japp, helt korrekt.
okej då är jag med så långt, sedan blir då resultatet efter att vi satt in gränsvärdena men vad gör vi sedan med resultatet?
Jag förstår inte vad du menar. Resultatet kan möjligtvis skrivas om i enklare form, men så mycket mer krävs inte att vi gör med det.
Däremot kan du göra mycket mer med själva uppgiften. T.ex. kan du se om du hittar en lämplig avbildning och beräkna integralen också på det sätt.
Exempel på lösningsgång avbildning:
Kan du hitta en smartare avbildning?
2x+2y har vi ju från början men var får du v=y-x ifrån? eller vad är motiveringen till att sätta v=y-x?
sedan är jag med på funktionaldeterminanten men inte riktigt gränsvärdena, hur får vi fram dom? sedan om man bryter ur x får man att vilket vi har inom ln istället för x så det är jag också med på.
Idil M skrev:2x+2y har vi ju från början men var får du v=y-x ifrån? eller vad är motiveringen till att sätta v=y-x?
På något sätt måste du komma åt integrationsområdet. y-x=a är den svarta linjen i denna Desmos-animation
Studera animationen, testa att själv dra i reglaget för a. Förstår du nu varför just v=y-x där v går från -3/2 till 3/2 fungerar?
okej jag kan se att vi får in hela integrationsområdet om vi sätter v=y-x med integrationsgränserna -3/2 till 3/2, men jag har fortfarande svårt att själv komma fram till gränserna -3/2 till 3/2 och sedan till 5.
Idil M skrev:okej jag kan se att vi får in hela integrationsområdet om vi sätter v=y-x med integrationsgränserna -3/2 till 3/2, men jag har fortfarande svårt att själv komma fram till gränserna -3/2 till 3/2 och sedan till 5.
Linjen och kurvan skär varandra i två punkter i det aktuella området, nämligen (2, 0.5) och (0.5, 2).
Alltså ska gå från
För punkt 1 (x=2, y=0.5),
För punkt 2 (x=0.5, y=2),
Intervallet för v är alltså .
Vilket du också kan se i animationen ovan.
Linjerna v=y-x och u=2x+2y är vinkelräta mot varandra. Givet att du vet v kan du bestämma mellan vilka värden u får variera för att hålla sig inom området.
Tanken var bara ett ge dig ett exempel på en avbildning, hur man beräknar integralen med en sådan och få dig att fundera över om det finns enklare / smartare avbildningar.
okej gör jag samma sak med u=2x+2y får jag gränsvärdet 5 både med x=2 y=0.5 och x=0.5 och y=2 därmed har vi den övre gränsen för u men den undre ska ju då bli
jag får att då v=-3/2 är u=5 men då v=3/2 blir u också 5 så jag förstår inte riktigt hur vi får
och sedan om jag förstår det rätt ska vi få att x= när vi sedan ska integrera
Idil M skrev:jag får att då v=-3/2 är u=5 men då v=3/2 blir u också 5 så jag förstår inte riktigt hur vi får
och sedan om jag förstår det rätt ska vi få att x= när vi sedan ska integrera
Hej Idil,
Vi har infört koordinatbytet
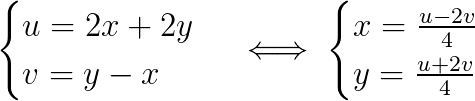
Variabeln v ska gå från till . För varje värde på v ska u gå från kurvan till linjen .
Gränslinjen är enkel, den är ju bara . För kurvan sätter vi in x och y enligt ovan:
Löser vi ut u (u>0) får vi:
Alltså ska u gå från till . Hela vår integral blir
när vi ska börja med själva beräkningen av dubbelintegralen, ska vi börja i v-led eftersom den undre gränsen för u beror på v?
i så fall kan vi då använda att den primitiva funktionen till är och sätta
Nej, eftersom gränsen innehåller ett uttryck med v är det bättre att integrera i u först och sedan i v.
Pedagogiskt sett känns det också som vi hamnat lite snett, min tanke var inte att du skulle lösa integralen med avbildningen jag gav som exempel utan att visa hur en avbildning fungerar med funktionaldeterminanten som skalfaktor, hur man tar fram gränserna samt få dig att fundera över om det finns smartare avbildningar.
Om du fortsätter på det inslagna spåret kommer du förvisso få en integral som går att lösa och som ger exakt samma svar () som vi fick här.
Men integralen kommer inte att vara lättare att beräkna än den ursprungliga integralen. Du måste bland annat utnyttja lite listiga specialknep.
okej, så det ska alltså finnas ett enklare sätt att komma fram till svaret genom en annan avbildning än den som vi har nu? tyvärr är jag inte helt säker på hur man gör för att få fram bättre avbildningar, hur är det meningen att man ska göra för få fram en smartare avbildning som gör det lättare för oss att lösa uppgiften?
hur ska man gå tillväga för att använda funktionaldeterminanten som skalfaktor? vi har ju räknat ut tidigare att funktionaldeterminanten blir
ett exempel på en avbildning är alltså u=2x+2y och v=y-x men man ska alltså med hjälp av J=1/4 kunna hitta någon bättre avbildning som underlättar beräkningen av integralen för oss?
jag är tyvärr fortfarande inte med på hur vi ska hitta en avbildning som gör beräkningen av integralen enklare än den vi hade med u=2x+2y och v=y-x, hur kan vi hitta en sådan avbildning? jag förstår inte riktigt hur vi ska gå tillväga för att komma framåt.
Albiki skrev:Integrationsområdet är alltså
Prova att införa variabler och .
Det är över en vecka sedan du fick det här tipset. Har du provat det?
då får jag att med och med variablerna u=x+y och v=xy får jag funktionaldeterminanten
när man sedan ska räkna ut gränsvärdena vet vi att linjen 2x+2y=5 och hyperbeln xy=1 skär varandra i punkterna (x=2, y=0.5) och (x=0.5, y=2)
för u får vi ju då gränsvärdena 3/2 men det blir ju samma gränsvärde oavsett om man väljer x=2 eller 0.5 och för v får vi gränsvärdet 1
Om man sätter får jag att och stoppar vi in x och y värdet i v=xy får vi att
Då får jag gränsvärderna för u som och det ena gränsvärdet för v bör väl vara 1 men det andra har jag inte kommit fram till än.
kan man ställa upp integralen som då vi får att v=



