Integralberäkning
Hej,
Denna e lite för svår, just nu, så behöver hjälp med den för förståelse.
Ett par mil öster om Ystad uppe på den 42 m höga Kåsebergaåsen, ligger Ales stenar. Stensättningen är 70 m lång, 18 m bred och består av 59 stenar. Stensättningens form har gjort att man länge trott att det var frågan om en skeppssättning från vikingatiden. Senare forskning tyder på att det kan vara en kultplats från bronsåldern.

Stenarnas placering som visas i figuren nedan kan antas följa två motställda parabler (= grafen till andragradsfunktioner). Din uppgift är att ta fram en lämplig funktion för en av parablerna och beräkna arean av det område som stenarna innesluter.
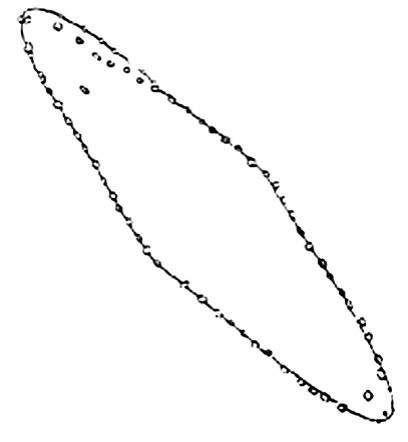
Hej.
Kan denna bild hjälpa?
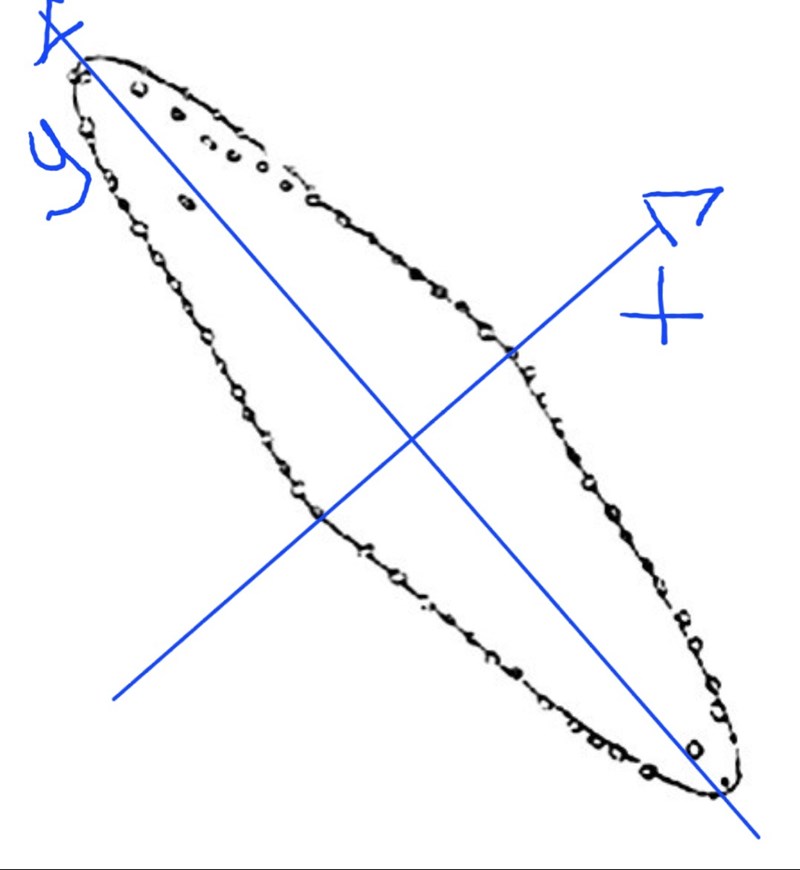
Hej Y,
Nej, förstår den inte. Har läst på om integraler, dvs arean under kurvan och beräkning av dem från en punkt till en annan,o sedan den primitiva fuknitonen, men kan inte tillämpa än så behöver förklaring steg för steg på sådan här tillämpningar av den.
Mvh/H
Hej. Det första steget, innan vi ens blandar in integraler, borde vara att försöka lista ut vilken funktion som det gäller. Har du några tankar om hur du ska göra det?
Henrik 2 skrev:Hej Y,
Nej, förstår den inte. Har läst på om integraler, dvs arean under kurvan och beräkning av dem från en punkt till en annan,o sedan den primitiva fuknitonen, men kan inte tillämpa än så behöver förklaring steg för steg på sådan här tillämpningar av den.
Mvh/H
Kan det här hjälpa?
Eftersom stensättningen är symmetrisk så behöver du bara beräkna arean av det streckade området. Den totala arean är sedan 4 gånger så stor.
Stenarnas placering för y > 0 bildar en parabel, dvs en andragradskurva.
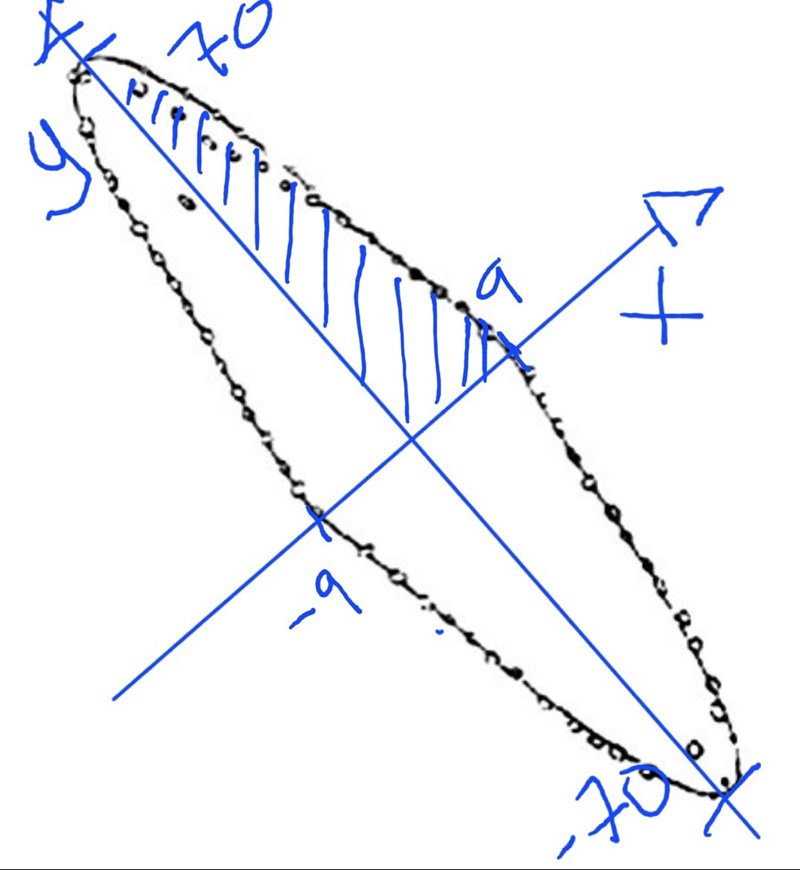
Funktionen.
Aha, precis nu förstår jag lite i vart fall. 70 m lång och 18 m bred. Så den ligger på detta sätt i en graf som bildar en parabel, dvs en andragradsfunktion. 70 m e y=höjden och 18 m e bredd som går mellan stenarna, från -9 til 9 , dvs 18 m. Ok, e med än så länge.
Integralen, dvs arean ligger under kurvan, du valde arean på den positiva sidan, kunde du lika gärna valt arean under grafen/parabeln på den negativa sidan?
Just det iom att alla områden e lika stora/symmetriska så *4.
Vad görs sedan då jag nu förstår detta..
Funktion blir x2 .....
Arean då blir vad,hur ställer man upp det? E integralen från vad.....
Jag skrev fel tidigare.
Så här ska det se ut. Maxvärdet på y är hälften av 70, dvs 35:
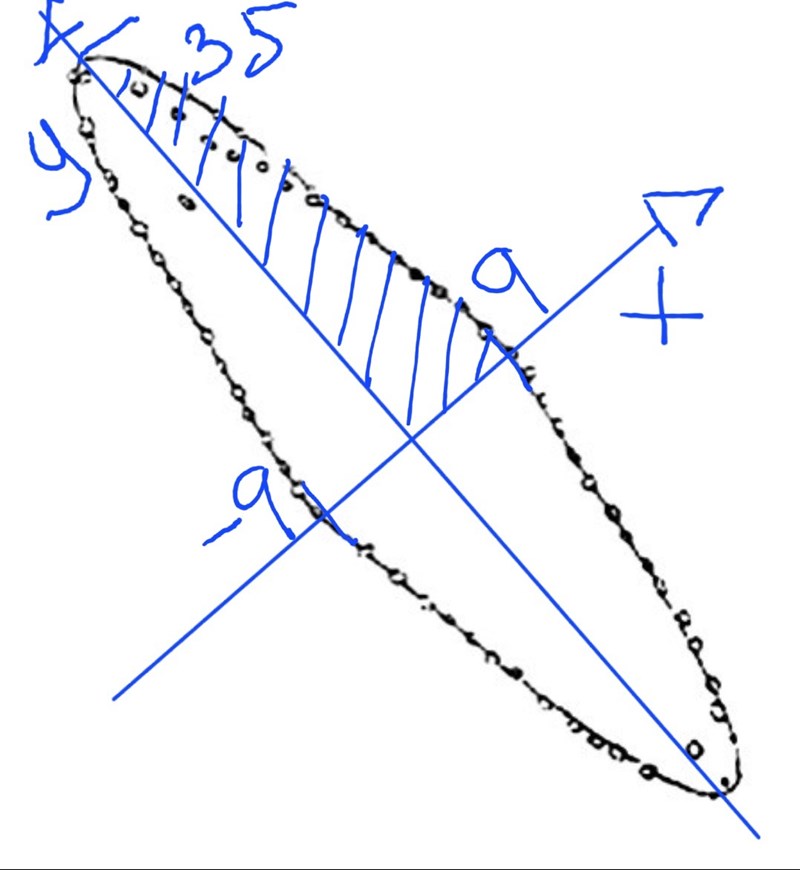
Du ska hitta en andragradsfunktion y = ax2+bx+c som har egenskaperna att
- symmetrilinjen är x = 0
- maximipunkten är (0, 35)
- nollställena ligger vid x = -9 och x = 9.
Det är denna funktion som du ska integrera från x = 0 till x = 9 och sedan multiplicera resultatet med 4.
=====
Och ja, det går även bra att istället beräkna arean under x-axeln. Detta eftersom stensättningen är symmetrisk både med avseende på x- och y-axeln.
Hej Y,
E med på nu hur du gör och att symmetrilinjen e x=0, maximip e (0,35) och nollställen e x=-9 och x=9
Men vet inte vad som ska göras nu. Ska jag hitta en andragradsfunktion, förstår inte hur jag ser det, kan du förklara tack. Jag vet inte hur man får ut en sådan av y = ax2+bx+c . C är konstant, vilken e det här? bx e ett tal med x, och ax2 då bildandet av andragradsfunktionen?
Sedan ska jag integrera från 0-9 och med det då hitta en primitiv funktion till 2:agradsfunktion,en antiderivata?
Mvh/H
Sättet att få a, b, och c är genom att sätta in dina kända värden för x och y i ekvationen. Då får du ett ekvationssystem på tre ekvationer som du kan lösa för att få variablerna.
Ok, i vilken, finns ingen mer än denna y = ax2+bx+c
Du menar utifrån maximip (0,35) eller dem andra värdena på x som e -9 och 9?
Mvh/H
Henrik 2 skrev:Ok, i vilken, finns ingen mer än denna y = ax2+bx+c
Du menar utifrån maximip (0,35) eller dem andra värdena på x som e -9 och 9?
Mvh/H
Kurvan är på formen
y=-Ax^2+35
där y(9)=0 vilket ger A=35/81
Henrik 2 skrev:Ok, i vilken, finns ingen mer än denna y = ax2+bx+c
Du menar utifrån maximip (0,35) eller dem andra värdena på x som e -9 och 9?
Mvh/H
Jag menar alla tre punkterna. Så här:
Generellt sett gäller att sambandet y = ax2+bx+c ska gälla för alla punkter på parabeln.
Du känner till de tre punkterna (0, 35), (-9, 0) och (9, 0).
Om du sätter in koordinaterna för var och en av dessa tre punkter i sambandet får du de tre ekvationerna
- 35 = a*02+b*0+c
- 0 = a*(-9)2+b*(-9)+c
- 0 = a*92+b*9+c
Den första ekvationen ger dig direkt att c = 35
De andra två ekvationerna blir då
- 0 = 81a-9b+35
- 0 = 81a+9b+35
Lös ut a och b ur detta linjära ekvationssystem så har du din funktion f(x) vars graf motsvarar parabeln.
Näsra steg är att integrera denna funktion från x = 0 till x = 9 och multiplicera resultatet med 4.
=====
Som Trinity2 påpekar så finns det en genväg till att hitta funktionsuttrycket, men jag tror att det är bra att du verkligen förstår det generella tillvägagångssättet att hitta de tre konstanterna a, b och c om du har tre givna punkter på en parabel.
Hej,
Ok, precis,ja kör på det generella så jag förstår processen o nöter in den innan genvägar tas, förstod inte den/det som Trinity gjorde än, behöver som du säger fört förstå den mer generella vägen.
Återkommer med försök på detta.
Tack/H
först.
Ok, får a = b/9-35/81 och b= 9a+35/9. Är det korrekt?
Man delar ju, väl, både 9b och 35 med 81 o sedan förkortade jag med 9 så det blev kvar b/9. Samma tänk för att få ut a. Men skulle man bara få a= 35/81 o b= 35/9?
Mvh/H
Du behöver räkna fram ett siffervärde för a och ett siffervärde för b. Sätt in det värde du får för a från den första ekvationen i den andra, så får du en ekvation som bara beror på b, och då kan du räkna ut värdet på b. När du vet värdet på b ka du sätta in det i antingen den första eller den andra ekvationen för att få fram a.
Hej,
Förstår att jag ska få ett siffervärde för a o b men e det korrekt vad som jag fått ?
Så a = b/9-35/81 sätter jag in i den andra för att få b och sedan får jag värdet på b och sätter in i den första för att få värdet på a.
Ok, testar.
/H
Hej.
Du har ett linjärt ekvationssystem som lyder
- 0 = 81a-9b+35
- 0 = 81a+9b+35
Du kan lösa det på flera olika sätt.
En enkel metod är att se att både första och andra ekvationen har 0 i vänsterledet, dvs de ör lika varandra.
Det betyder att även de båda högerleden måste vara lika varandra.
Det ger oss ekvationen 81a-9b+35 = 81a+9b+35
Lös nu ut b ur den ekvationen.
Använd sedan detta värde på b för att lösa ut a ur någon av de två ursprungsekvationerna.
Visa varje litet steg i din uträkning.
Ok,tack .Gjorde precis som S sade men fick helt fel på det. Så tack , man sätter dem mot varandra för att få ut b o sedan får man ut a. Jag testar..
Nee, jag sätter dem mot varandra och flyttar över b till ena sidan och a och talet till den andra o då får jg antingen -18b eller 18b. Hur får jag ut b om jag inte ska göra så?
/H
Du ska inte "flytta" saker, risken för fel är då alldeles för stor.
Du ska istället använda balansering, i det här fallet addera eller subtrahera termer till/från både VL (dvs vänsterledet) och HL (dvs högerledet).
Läs gärna igenom dessa avsnitt som beskriver ekvationslösning med hjälp av balansering. Fråga sedan oss om allt du vill att vi förklarar närmare
Återigen: Visa varje liter steg i din uträkning. Då kommer detta att gå mycket snabbare eftersom vi då omedelbart ser eventuella feltänk/felräkningar.
Balansering,k, får kika länk om det. Men man gör väl så att man flyttar över från VL eller HL för att få variabel ensam?
Mvh/H
Men det e ju preci så jag gör (väl) o menar?
81a-9b+35 = 81a+9b+35
81a-9b+9b+35=81a+9b+9b+35
81a+35=81a-81a+18b+35-35
81a-81a+35-35=18b
0=18b?
Vad gör jag för fel?
Mvh/H
Precis
Ok, visat nu..:)
Henrik 2 skrev:Men det e ju preci så jag gör (väl) o menar?
81a-9b+35 = 81a+9b+35
OK, bra.
81a-9b+9b+35=81a+9b+9b+35
Bra, här adderar du 9b till båda sidor. Det är rätt.
81a+35=81a-81a+18b+35-35
Men här subtraherar du 81a och 35 från HL utan att göra samma sak i VL. Det är fel, för då gäller inte likheten längre.
81a-81a+35-35=18b
Och här gör du samma fel fast i VL, dvs du subtraherar 81a och 35 från VL utan att göra samma sak i HL.
Men eftersom du gjorde två fel som tar ut varandra så blir nästa rad ändå rätt.
0=18b?
Som jag skrev ovan, detta är rätt trots felen. Se nedan för fortsättning.
Vad gör jag för fel?
Se ovan
=========
Förslag på hur du kan skriva en tydlig ekvationslösning med låg risk för fel:
81a-9b+35 = 81a+9b+35
Subtrahera 35 från båda sidor:
81a-9b+35-35 = 81a+9b+35-35
Förenkla:
81a-9b = 81a+9b
Addera 9b till båda sidor:
81a-9b+9b = 81a+9b+9b
Förenkla:
81a = 81a+18b
Subtrahera 81a från båda sidor:
81a-81a = 81a+18b-81a
Förenkla:
0 = 18b
Dividera båda sidor med 18:
0/18 = 18b/18
Förenkla:
0 = b
Vi har nu kommit fram till att b = 0.
Sätt nu in det i ekvationen 0 = 81a-9b+35 och lös ut a.
Använd samma tydliga steg-för-steglösning som jag föreslog (där du beskriver vad du ska göra innan du gör det) och visa varje steg.
Men Y, då gör jag rätt, sätter inte jämt ut det utan går på steg 2, då jag tänker ut det i huvudet.
Ska man ta 0/18=b för att få det fritt,ok. Så det blir att b=0
Ok, då testar jag att ta in det i ena ekvationen för att få ut a.
81a-9b+35= 81a-9*0+35
81a-0+35= 81a=-35
a=-35/81
y = ax2+bx+c
Så funktionen blir då y= -35/812 + 35?
Denna ska integreras ,menas det att hitta en primitiv funktion till den?
Sist *4 för 4 st lika stora områden i parabeln=arean.
Henrik 2 skrev:Men Y, då gör jag rätt, sätter inte jämt ut det utan går på steg 2, då jag tänker ut det i huvudet.
Det du tänker kanske är rätt, om du nu tänker 2 steg framåt i huvudet. Men det du skriver är inte rätt.
Jag rekommenderar starkt att du inte tänker 2 steg framåt i huvudet utan att du istället tar ett litet steg i taget och att du skriver ner varje steg.
Om du tar flr stora tankesteg i huvuvet så är dels risken för fel alltför stor, dels så gör du det i stort sett omöjligt för dig själv att i efterskott kontrollera dina lösningar.
Ska man ta 0/18=b för att få det fritt,ok. Så det blir att b=0
Ja, det stämmer.
Ok, då testar jag att ta in det i ena ekvationen för att få ut a.
81a-9b+35= 81a-9*0+35
Nej, du ska skriva ut både VL och HL i ekvationen, alltså
0 = 81a-9b+35.
Du vet att b = 0, vilket ger dig ekvationen
0 = 81a-9*0+35
Förenkla:
0 = 81a+35
Subtrahera 35 från båda sidor:
0-35 = 81a+35-35
Förenkla:
-35 = 81a
Dividera båda sidor med 81:
-35/81 = 81a/81
Förenkla:
-35/81 = a
81a-0+35= 81a=-35
a=-35/81
Återigen kom du fram till rätt svar trots att du skriver fel.
Du kanske tänker annorlunda än standardsättet, vilket kan vara OK. Men du måste du beskriva hur du tänker så att du inte riskerar poängavdrag på uppgifter.
Henrik 2 skrev:y = ax2+bx+c
Så funktionen blir då y= -35/812 + 35?
Nej, här glömmer du ett x2
Det står att a ska multipliceras ned x2.
Detta ger dig y = -35/81x2+35
Denna ska integreras ,menas det att hitta en primitiv funktion till den?
Ja
Sist *4 för 4 st lika stora områden i parabeln=arean.
Ja
Henrik 2 skrev:Hej,
Ok, precis,ja kör på det generella så jag förstår processen o nöter in den innan genvägar tas, förstod inte den/det som Trinity gjorde än, behöver som du säger fört förstå den mer generella vägen.
Återkommer med försök på detta.
Tack/H
En parabel som är symmetrisk runt origo har ingen x-term. Om ett andragradsuttryck har en x-term kommer kvadratkompletteringen att innehålla en förskjutning i sidled, t.ex.
x^2-2x+2=(x-1)^2+1
Aktuell parabel är symmetrisk i x-led runt origo och därmed på formen ax^2+b.
För x=0 har vi y=35 varför b=35
Sedan är parabeln konvex varför a<0.
Kvar är att bestämma a och då parabeln har ett nollställe i t.ex. 9 har vi att
a*9^2+35=0
vilket ger a=-35/81.
Trinity2 skrev:[...]
Sedan är parabeln konvex varför a<0.
Du menar väl konkav?
Yngve skrev:Trinity2 skrev:[...]
Sedan är parabeln konvex varför a<0.
Du menar väl konkav?
Ja, konkav, felskrivning.
Hej,
Hm, jag kör på det enkla sättet, läste din förklaring Trinity, ska försöka ta till mig den när grunderna sitter mer, dock f örstår jag på ett ungefär vad du menar. Så konkav e den med maxp.
Just det tog inte med x.:t ser det nu, yes. Y, jag tänker rätt hör men skriver inte ut i HL eller VL utan hoppar det steget i huvudet,enkel räkning, men visst kaske får fel ibland när jag gör på det sättet, men här e det så pass ekelt så då an man göra det.
Så denna ska jag hitta en primitiv funktion till -35/81x2+35 och sedan integrera från 0-9?
Så då ska vi se om jag kan få ut en primitiv funktion av det dx.
Vet inte hur den ser ut men försöker mig på det, säkerligen fel men här e det: Har inte sett en primitiv funktion av ett sådant tal så kan det inte, än.
klammer -35x/81x3 +35x
här
kan
klammer -35x/81x3 +35x klammer
sedan ta den primitiva funktionen, som säkerligen e fel, ni får rätta mig, och stoppa in först 9 i den och sedan - 0 o då får man.....
Mvh/H
Henrik 2 skrev:[...]
Just det tog inte med x.:t ser det nu, yes. Y, jag tänker rätt hör men skriver inte ut i HL eller VL utan hoppar det steget i huvudet,enkel räkning, men visst kaske får fel ibland när jag gör på det sättet, men här e det så pass ekelt så då an man göra det.
OK, men tänk på att det är viktigt att skriva lösningar så att de är enkla att följa, både för läraren och här på PA.
Dessutom blir det svårt för dig att kontrollera dina egna lösningar om de inte är tydliga.
Så denna ska jag hitta en primitiv funktion till -35/81x2+35 och sedan integrera från 0-9?
Så då ska vi se om jag kan få ut en primitiv funktion av det dx.
Vet inte hur den ser ut men försöker mig på det, säkerligen fel men här e det: Har inte sett en primitiv funktion av ett sådant tal så kan det inte, än.
klammer -35x/81x3 +35x
Ett bra tips för att hitta en primitiv funktion F(x) till en funktion f(x) är att iterera "Gissa", "Pröva", "Modifiera" tills du hittar rätt.
Vi har
Steg 1: Gissa.
Vi gissar att
Steg 2: Pröva
Vi deriverar vårt förslag på och får då
Detta är inte helt rätt. Den första termen är en faktor 3 för stor men den andra termen är rätt.
Steg 3: Modifiera
Eftersom den första termen var en faktor 3 för stor så blir den första termen i vår nya gissning en faktor 3 mindre för att kompensera.
Ny gissning:
.
Pröva:
Vi deriverar vårt förslag på och får då
Det stämmer med .
Därför är en primitiv funktion till .
Tillägg: 20 mar 2024 10:50
Jag råkade skriva 18 istället för 81 i en nämnare.
här
kanske
enkelt.
Hej Y,
Ok, så just det skulle ta x3 /3 treorna tar ut varandra när man deriverar,men nästan rätt,hehe. Jo, sant handlar om kommunikationspoäng,så verkar som man måste vara övertydlig, oavsett för vems skull.
Då har vi den primitiva funktionen så då integrering av 0 till 9 i denna.
−35/81⋅x3 /3+35x inom klammerparentes.
Ska vi se här. Tror inte detta e rätt,tur att man har er som kan hjälpa en när ni ser att man försöker. Sätter först in x=9 sedan x=0 , tar det minus.
-35/81* 93 =729/3+35*9
Tar nämnaren i -35/81 och delar med 9=81/9 = 9 o tar täljaren i 93 delat med 9=729/9=81 o så kan man förkorta ytterliggare o tar nämnaren 9/9=1 och täljaren 81/9=9 som i sin tur kan tas 9/3=3 + 315
Då får man -35*3+315=210
Tar nu o sätter in 0 som man tar 210- ....med.
Får -35/81*03 /3+35*0 = -35/81
Då har man 210/1-(-35/81) .
Vet inte om man ska göra om 210 till 81:e delar men om så:
210*81 =17010+35/81= 17045/81= 210.4 ca
Jag har ingen aning huruvida detta var rätt ,eller något var rätt..:)
Tur man har er just nu..
Mvh/H
Jag förstår inte dina uträkningar och ditt resultat stämmer bara nästan.
Det verkar som att du räknar att 03/3 är lika med 1? Men det är lika med 0.
Jag föreslår att du försöker härma våra sätt att skriva lösningar.
Förslag för denna uppgift:
Vi har konstaterat att , vilket vi kan skriva som
Vi har konstaterat att en primitiv funktion till detta är , vilket kan skrivas
Vi vill nu beräkna integralen , vilket är lika med .
Vi får då integralens värde
Multiplicera nu detta med 4 för att få fram svaret.
Hej Y,
Tack, för detta. Då fick jag fram nästan det rätta svaret med mina beräkningar som e korrekta,dock så förstår du dem inte då jag räknar på ett annat sätt än du här plus att jag inte e tydlig i min kommunikation och sätter ut det man skall steg för steg, men får löra mig det o nöta in det förhoppningsvis till NP om x antal veckor.
Ok, så man sätter 35 x först istället för i slutet och sedan så iom 9 upphöjt till 3 så gör du om 81 till 9 upphöjt till 2 så det blir kvar i täljaren 35*9/3=105 . Så 315-105=210
Jag tog inte att 0 upphöjt till 3/0 var 1,det var en annan sak som jag gjorde ,var med på att hla den parentesen med integranden 0 blev 0.
Så nu då 210*4=840 som blir arean och funktionen är den primitiva är 35x−35/81⋅x3/3?
hela
Henrik 2 skrev:Hej Y,
Tack, för detta. Då fick jag fram nästan det rätta svaret med mina beräkningar som e korrekta.
Med den del av dina beräkningar som var korrekta fick du fram rätt delresultat. Med de delar av dina beräkningar som inte var korrekta tillkom ett fel.
dock så förstår du dem inte då jag räknar på ett annat sätt än du här plus att jag inte e tydlig i min kommunikation och sätter ut det man skall steg för steg, men får löra mig det o nöta in det förhoppningsvis till NP om x antal veckor.
OK, det låter bra. Vi får vara tålmodiga med varandra.
Ok, så man sätter 35 x först istället för i slutet och sedan så iom 9 upphöjt till 3 så gör du om 81 till 9 upphöjt till 2 så det blir kvar i täljaren 35*9/3=105 . Så 315-105=210
Ja, just så.
Jag tog inte att 0 upphöjt till 3/0 var 1,det var en annan sak som jag gjorde ,var med på att hla den parentesen med integranden 0 blev 0.
OK, bra
Så nu då 210*4=840 som blir arean och funktionen är den primitiva är 35x−35/81⋅x3/3?
Ja, det stämmer.
Härligt,
Efter mycket om o men o min förståelse för denna, som var svår tycker jag då man inte vad som skall göras, så förstår jag den och med din hjälp steg för steg e jag med, och har faktiskt kommit fram med egna beräkningar, mer eller mindre, till korrekt svar men dina steg krävdes för denna förståelse.
Mvh/H
Toppen. Tack för återkoppling.
Yes, skrev till dig privat om din pedagogik som passar mig.Jag får tänka men du förklarar stegen pedagogiskt,precis dem grunderna som du vet att man behöver. Vissa här på forumet har väl inte samma, enligt mig, förståelse för den pedagogiken. Du ska inte direkt ge mig svaren,utan jag ska försöka själv som jag gör, men när jag fastnar ger du mig steg/lösning,och generellt sett förstår jag den, då den e grundläggande.
Mvh/H



