43 svar

374 visningar

Viktorini behöver inte mer hjälp

Integraler

Hej,

Rita upp kurvan y = 4-x^2 x > 0 Rita sedan en linje mellan kurvans skärningspunkt
med y-axeln och dess skärningspunkt med x-axeln. Härvid uppkommer två st areor.
Beräkna förhållandet mellan dessa båda areor.
 Gör om detta på samma sätt, fast med kurvan y = 5-x^2

Är osäker på om jag har tänkt rätt på den med y=5-x^2

För triangeln som bildas blir arean $(5 * \sqrt{5)} / 2$ .

För området mellan linjen och parabeln blir arean:

$\int_{0}^{\sqrt{5}} (5 - x^{2}) d x = 9$

Och sedan 9-4=5 för att inte få med triangeln.

Blir förhållandet då 4:5???

Flyttar tråden från Fysik till Ma3, där den verkar höra hemma. /Smaragdalena, moderator

Arbetar du med 4-x^2 eller 5-x^2? Integralen blir inte 9. Vad är det för 4 som du drar bort från 9? Är det trianglens area när du har 4-x^2?

Det är två olika, den med 4-x^2 har jag redan räknat ut. Den med 5-x ^2 är en annan uppgift men det står att man ska göra på samma sätt.

När man ritar upp det som de beskriver i texten får man ju en triangel och ett områden mellan parabeln och triangelns hypotenusa. Triangelns area fick jag till 4 när jag tog b*h/2. Sedan för att få området mellan parabeln och linjen så måste jag ju räkna ut först hela området och sedan subtrahera triangeln.

Viktorini skrev:
Det är två olika, den med 4-x^2 har jag redan räknat ut. Den med 5-x ^2 är en annan uppgift men det står att man ska göra på samma sätt.
När man ritar upp det som de beskriver i texten får man ju en triangel och ett områden mellan parabeln och triangelns hypotenusa. Triangelns area fick jag till 4 när jag tog b*h/2. Sedan för att få området mellan parabeln och linjen så måste jag ju räkna ut först hela området och sedan subtrahera triangeln.

Triangeln med area 4 hör till första uppgiften, varför använder du den i andra uppgiften?

Du får även fel värde på integralen. Visa hur du beräknar den så kan vi hjälpa dig att hitta felet.

Okej: $[5 x - x^{3} / 3] \frac{\sqrt{5}}{0} (d i v i t i o n t e c k n e t m e l l a n 5 o c h n o l l s k a i n t e v a r a d ä r m e n v i s s t e i n t e h u r j a g s k u l l e s k r i v a u \tan . D e t t a ä r d e n p r i m i t i v a f u n k t i o n e n$

$5 \sqrt{5} - (\sqrt{5})^{3} / 3 = 11 - (5 / 3) = 9$

Viktorini skrev:
Okej: $[5 x - x^{3} / 3] \frac{\sqrt{5}}{0} (d i v i t i o n t e c k n e t m e l l a n 5 o c h n o l l s k a i n t e v a r a d ä r m e n v i s s t e i n t e h u r j a g s k u l l e s k r i v a u \tan . D e t t a ä r d e n p r i m i t i v a f u n k t i o n e n$
$5 \sqrt{5} - (\sqrt{5})^{3} / 3 = 11 - (5 / 3) = 9$

Aha bra då förstår jag. Felet är att du avrundar dina (del)resultat. Använd exakta värden istället.

Okej, då fick jag istället området mellan parabeln och linjen till: 3,5

Så förhållandet är 4:3,5???

Om du har räknat de båda areorna rätt (jag har inte kollat) så är det snyggare att skriva förhållandet som heltal, d v s 8:7.

EDIT: Nu räknade jag ut uppgiften med $5-x^2$ , och mina siffror har inga likheter med dina. Förhållandet blev också ett helt annat (men snyggt).

Viktorini skrev:
Okej, då fick jag istället området mellan parabeln och linjen till: 3,5
Så förhållandet är 4:3,5???

Nej hur fick du fram de talen?

Visa din figur, vilka områden du areaberäknar och hur du areaberäknar dem.

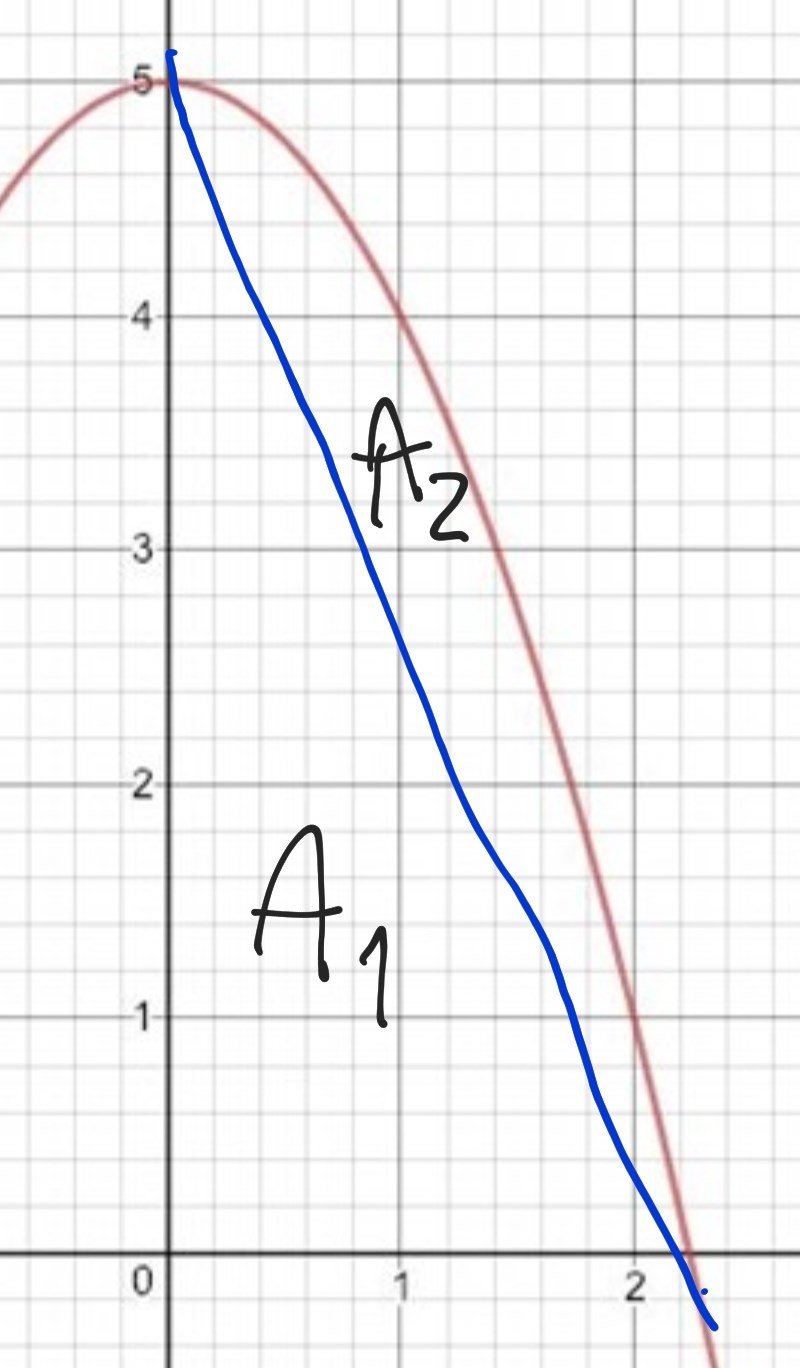
Här är ju själva grafen. Jag skulle rita en linje mellan kurvans skärningspunkt med y-axeln och dess skärningspunkt med x-axeln. Då bildas det en triangel, A1.

Arean för den får man när man tar b*h/2. För att få basen:

0 = 5-x^2

$x = \sqrt{5}$

A1 = $5 \times \sqrt{5} / 2 = 5, 59017$

För att få arean mellan parabeln och linjen får jag först räkna ut arean under hela parabeln och sedan subtrahera den med arean för triangeln.

A2= $\int_{0}^{\sqrt{5}} (5 x - x^{3} / 3) = 5 \sqrt{5} - ({\sqrt{5)}}^{3} / 3 = 7, 4535$

7,45356-5,59017=1,86339

Räkna exakt! Avrunda inte. Vilka areor får du då?

Som jag skrev i detta svar: Avrunda inte! Räkna med exakta värden.

Tips:

$(\sqrt{5})^3=5\sqrt{5}$

Och om du (någon annan gång) avrundar så måste du använda tecknet "ungefär lika med", dvs $\approx$ istället för likhetstecken.

Jag ändrade om där uppe, men känns som det fortfarande blir jätte tokigt?

Viktorini skrev:
Jag ändrade om där uppe, men känns som det fortfarande blir jätte tokigt?

$5\sqrt{5}$ är ett exakt värde.

$11.18033989$ är ett avrundat värde, dvs ett närmevärde till $5\sqrt{5}$ .

Du ska inte använda avrundade värden.

Du ska använda exakta värden.

Förstår du skillnaden?

Okej då förstår jag skillnaden. Men hur ska jag räkna ut integralen med de exakta värdena?

Viktorini skrev:
Okej då förstår jag skillnaden. Men hur ska jag räkna ut integralen med de exakta värdena?

Jamen det har du ju redan gjort!

I detta inlägg.

Arean $A_1=\frac{5\sqrt{5}}{2}$

Arean $A_2$ är lika med integralen av $5-x^2$ från $x=0$ till $x=\sqrt{5}$ minus $A_1$ .

Så att integralen blir 9 stämmer?

Då tar jag 9 subtraherat med arean för triangeln för att få området mellan parabeln och linjen? Alltså:

9-(5* $\sqrt{5}$ / 2)

Viktorini skrev:
Så att integralen blir 9 stämmer?
Då tar jag 9 subtraherat med arean för triangeln för att få området mellan parabeln och linjen? Alltså:
9-(5* $\sqrt{5}$ / 2)

Nej det blir inte 9.

9 är inte ett exakt värde. 9 är ett närmevärde, dvs ett avrundat värde.

Nu säger vi för femte gången: Du ska inte avrunda dina värden.

Integralens värde är $5\sqrt{5}-\frac{(\sqrt{5})^3}{3}$ , precis som du redan har räknat fram det. Men sen ska du förenkla det uttrycket, inte ta fram ett närmevärde till det.

$(\sqrt{5)^{3}} - ((\sqrt{5)^{3}} / 3)$

Viktorini skrev:
$(\sqrt{5)^{3}} - ((\sqrt{5)^{3}} / 3)$

Jag antar att du menar $(\sqrt{5})^3-\frac{(\sqrt{5})^3}{3}$ och i så fall är det rätt värde på integralen.

Men sen kan du göra dessa två termer liknämniga och sätta dem på gemensamt bråkstreck innan du fortsätter.

Men ska jag då förlänga så de får samma nämnare? $3 * ({\sqrt{5)}}^{3} / 3 - ({\sqrt{5)}}^{3} / 3$

Viktorini skrev:
Men ska jag då förlänga så de får samma nämnare? $3 * ({\sqrt{5)}}^{3} / 3 - ({\sqrt{5)}}^{3} / 3$

Ja.

För att slippa exponenten kan du skriva $5\sqrt{5}$ istället för $(\sqrt{5})^3$ .

Så jag kan skriva det såhär:

$3 (5 \sqrt{5)} - (5 \sqrt{5}) / 3$

Viktorini skrev:
Så jag kan skriva det såhär:
$3 (5 \sqrt{5)} - (5 \sqrt{5}) / 3$

Ja om du menar $(3\cdot 5\sqrt{5}-5\sqrt{5})/3$ , dvs att täljren innehåller två termer (du glömde alltså parenteser runt täljaren).

Ja:

$(15 \sqrt{5} - 5 \sqrt{5}) / 3$

Men hur ska jag räkna vidare om jag ska behålla det exakta värdet?

Viktorini skrev:
Ja:
$(15 \sqrt{5} - 5 \sqrt{5}) / 3$

Men hur ska jag räkna vidare om jag ska behålla det exakta värdet?

Förenkla färdigt så blir det $\frac{10 \sqrt{5}}{3}$ . Vad tänker du göra med det värdet?

Ska jag då ta det subtraherat med arean för A1 för att få arean för A2:

$(10 \sqrt{5} / 3) - (5 \sqrt{5} / 2)$

Och sedan förlänga till samma nämnare?

Viktorini skrev:
Ska jag då ta det subtraherat med arean för A1 för att få arean för A2:
$(10 \sqrt{5} / 3) - (5 \sqrt{5} / 2)$
Och sedan förlänga till samma nämnare?

Just det.

Viktorini skrev:
Ska jag då ta det subtraherat med arean för A1 för att få arean för A2:
$(10 \sqrt{5} / 3) - (5 \sqrt{5} / 2)$
Och sedan förlänga till samma nämnare?

Ja. Om du tycker att $\sqrt{5}$ är svårt att räkna med så kan du tillfälligt byta ut det mot en symbol, t.ex. $a$ .

Då blir ditt uttryck $\frac{10a}{3}-\frac{5a}{2}$ .

Visa hur du gör för att förenkla det.

Okej, jag förlänger till samma nämnare då.

$(20 \sqrt{5} - 15 \sqrt{5)} / 6$

Viktorini skrev:
Okej, jag förlänger till samma nämnare då.
$(20 \sqrt{5} - 15 \sqrt{5)} / 6$

Vad ska du göra sedan med värdet?

Jag kan väll inte förenkla längre?

Viktorini skrev:
Jag kan väll inte förenkla längre?

Jo, det kan du, du kan dra 15 från 20. Men jag frågade vad du vill göra med värdet. Är du klar?

Men vad blir det då för tecken mellan: $5 \sqrt{5} ? \sqrt{5} / 6$

Nej jag är inte klar, ska kolla på förhållandet sen också.

Viktorini skrev:
Jag kan väll inte förenkla längre?

Detta är mycket enklare än vad du tror.

Jag tror att du blir förvirrad av att det står $\sqrt{5}$ i uttrycket.

Mitt råd är att du tillfälligt byter ut det mot något som är mer bekant, t.ex. $a$ .

Med $a=\sqrt{5}$ så blir uttrycket istället $\frac{20a-15a}{6}$ .

Visst kan du förenkla det?

Viktorini skrev:
Men vad blir det då för tecken mellan: $5 \sqrt{5} ? \sqrt{5} / 6$

Det här uppfattar jag som grundskolematte. Om du har 20 grejer och drar bort 15 sådana grejer, så har du 5 sådana grejer kvar. Här är grejen roten ur 5.

Okej, då blir det istället

$5 a / 6 = 5 \sqrt{5} / 6$

Nu är

A1 $5 \sqrt{5} / 2$

A2 $5 \sqrt{5} / 6$

Så A1 är tre gånger så stor som A2?

Viktorini skrev:
Nu är
A1 $5 \sqrt{5} / 2$
A2 $5 \sqrt{5} / 6$
Så A1 är tre gånger så stor som A2?

Det stämmer. Vad fick du när du gjorde det med 4-x^2?

Då fick jag samma, alltså att triangeln (A1) är tre gånger så stor som den andra arean!

Bra!

Visst var det enklare än du trodde?

Läs nu igenom denna tråd en gång till och fundera på vad du fastnade på, varför du gjorde det och hur vi hade kunnat hjälpa dig förbi dessa hinder på ett bättre sätt.

Jag tyckte ni svarade jättebra. Det var bara jag som var lite trög! Tack så jättemycket för hjälpen.

Blir det samma resultat eftersom lutningen är samma?

Viktorini skrev:
Jag tyckte ni svarade jättebra. Det var bara jag som var lite trög! Tack så jättemycket för hjälpen.
Blir det samma resultat eftersom lutningen är samma?

Nej, lutningen är inte samma.

Linjens lutning i a-uppgiften är $-2$

Linjens lutning i b-uppgiften är $-\frac{5}{\sqrt{5}}\approx -2,24$

Svara

Visa senaste svar