Integraler och vänster/högerkant
Hej! Jag har löst denna uppgiften och fick svaret till:
Visa spoiler
(-64/27)
Men jag har en hel del frågor (kanske mer generella idk):
1. Måste man rita en bild för att förstå få rätt funktion subtraherat med den andra?
2. Hur bestämmer man rätt gränser (varför kan jag liksom inte börja i 0)?
3. Hur funkar denna metoden egentligen? Är det lodrätt, horisontell integrering? Hur vet man?
4. Kan jag inte bara dela upp D (som är en kompakt mängd) i andra områden (d.v.s ). Om det bara komplicerar saker i detta sammanhanget, när ska man då dela upp i mindre områden. Detta är väl inte reguljära områden?
5. Hur vet man vad som är högra kant och vänstra kant? (antar att det kan vara upp och ner också). Är det ens rätt tänkt eller ska man göra på annat sätt (denna tekniken kom från Chatgpt, sen fick vi f1(x)-f2(x))?
6. Måste man veta skärningspunkterna? (varför räcker det bara med det ena värdet, jag har bara värdet för y i min uträkning men jag räknade även ut för x-värdet).

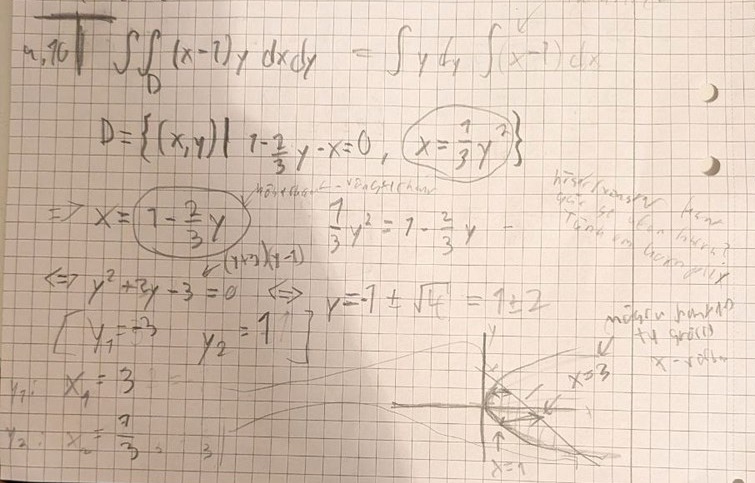
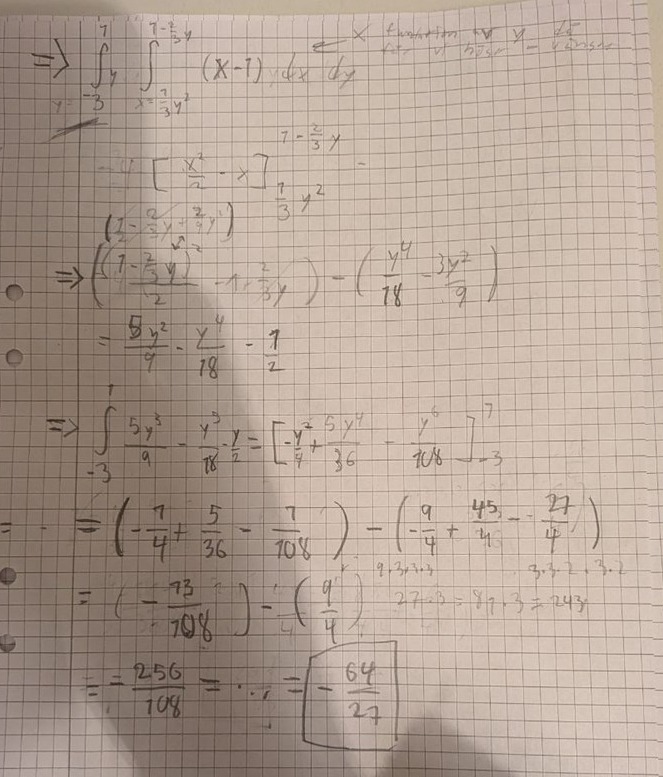
Många frågor på en gång.
Det tråkiga svaret är: Du kan göra hur du vill, bara så länge det är rätt. Du kan dela upp det i delområden, integrera vertikalt eller horisontellt. Det finns inte en väg, det finns olika vägar.
Men ditt svar verkar vara rätt, så du har gjort rätt, på något sätt iaf.
:((((
Jag vill att det ska vara mer konkret lmao!
Asså jag gillar att det finns alternativ men det är också dåligt på ett sätt för då måste man hålla koll på alla 75000 alternativ/verktyg lol.
Sykey skrev::((((
Jag vill att det ska vara mer konkret lmao!
Asså jag gillar att det finns alternativ men det är också dåligt på ett sätt för då måste man hålla koll på alla 75000 alternativ/verktyg lol.
Dubbelintegraler följer ett par "mönster"
1. Rakt på. Yttre i x-led, inre i y-led
2. Lite mera kluriga - man vänder på den "vanliga" ordningen och har yttre i y-led och inre i x-ld
3. 2-dim variabel-byte. Brukar anges som ledning eller om det är 4 räta linjer som spänner upp en parallellogram.
4. Polära koordinater. Finner du "x^2+y^2" i uttrycket kan du misstänka detta.
Ofta blir det inte svårare än så (men det räcker för många i början). Lös 20 av varje och du har sett det mesta - det finns inte så stor variation.
Ibland kan områdena och uttrycken svara svåra att överblicka - då kan man ana att integranden är udda och området är symmetriskt och allt blir 0... Ett klassiskt trick.
I ett fåtal fall kan man återfå samma integral igen med någon faktor och får på så sätt en integralekvation, men det händer inte så ofta, iaf inte på för "godkänt-poäng" skulle jag tro.
Mhm... aa den med parallellogrammet har jag stött på faktiskt... det svåra med dem (för mig) är att bestämma gränserna, för oftast får man bara linjerna.
Aa det där med udda/jämn och symmetri och sånt... asså sånt där fattar jag inte riktigt... är det sånt man måste rita upp funktionen för att se eller räcker det med denna
f(x)=f(-x) jämn
f(-x)=-f(x) udda
Eller lär man bara snappa upp sånt ju mer man gör? My goodness det kanske verkar självklart när jag skriver det men åndå hehe.
Sykey skrev:Mhm... aa den med parallellogrammet har jag stött på faktiskt... det svåra med dem (för mig) är att bestämma gränserna, för oftast får man bara linjerna.
Aa det där med udda/jämn och symmetri och sånt... asså sånt där fattar jag inte riktigt... är det sånt man måste rita upp funktionen för att se eller räcker det med denna
f(x)=f(-x) jämn
f(-x)=-f(x) udda
Eller lär man bara snappa upp sånt ju mer man gör? My goodness det kanske verkar självklart när jag skriver det men åndå hehe.
Tag t.ex. integralen av xy på halvcirkelskivan {x^2+y^2=r^2, y≥0} (radien spelar ingen roll). Vad kan du säga om integralens värde?
ahh that's a trick question för den säger inget om x-värdet!
Sykey skrev:ahh that's a trick question för den säger inget om x-värdet!
Nja, x är väldefinierat genom området, så även y, men om vi tar t.ex. punkten (1,1) (som ger "bidraget" 1*1 till Riemannsumman) så finns även punkten (-1,1) som ger bidraget = ? - och vad blir det om man summerar dessa?
Jfr med integralen
INT_{-R}^{R} x dx
där R>0. Du behöver inte räkna ut den. Du kan säga direkt vad den är.
Bidraget blir -1, summan 0?
Oo you mf...
den andra blir också 0... mhm... detta är nytt för mig så det känns lite konstigt men okej.
Men vet inte riktigt vad du menar med att den bidrar till Riemannsumman samt så fattar jag inte hur du kan ta punkten (1,1) eller (-1,1), de är ju båda utanför enhetscirkeln? Eller kör vi bara en annan funktion helt nu lol... eller nej vänta då är ju radien , men det spelade ju ingen roll. Men det du ville att jag skulle säga om integralens värde för cirkeln är (antar jag) att den är 0? Det känns konstigt om det är svaret eftersom det finns ju uppenbarligen en area men jag antar eftersom att den är centrerad så finns det vissa delar som hamnar på negativa axlar?
Bäckdahls dugga? 😅
ingenjören skrev:Bäckdahls dugga? 😅
*Uhum*...


