5
svar
74
visningar
Aorta är nöjd med hjälpen
Integraler trigonometri
Hej! Jag lyckas inte komma på hur facit har gjort denna omskrivningen (om mitt svar är rätt och det bara är en förenkling som saknas). Kan någon hjälpa mig?

Jag ser inte att ditt svar ska kunna förenklas till det som står i facit.
Men hur lyder uppgiften?
Det är uppgift b. 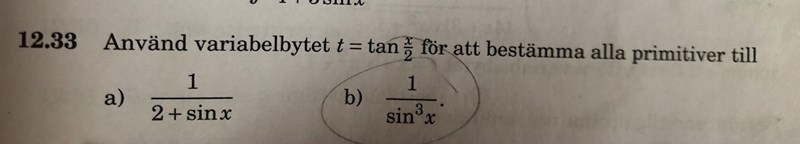

Jag förstår inte din uträkning.
Du börjar med att visa att
Kommentar: Detta gäller endast då , dvs då
Sedan substituerar du , vilket ger dig att .
Men vad händer sen?
Jag ber om ursäkt för den slarvigt skrivna uträkningen. När jag skulle renskriva den märkte jag en miss och knäckte därefter nöten.
Tack för hjälpen!
Ingen fara. Bra att du knäckte den.


