Integrationsgränser för dubbelintegral
Kan någon hjälpa mig med integrationsgränserna för denna funktion ,
jag misstänker att jag ska dela upp den i två integraler, dvs jag bryter isär dem mellan e-termerna.
Jag har ritat en figur som kan vara till hjälp också:
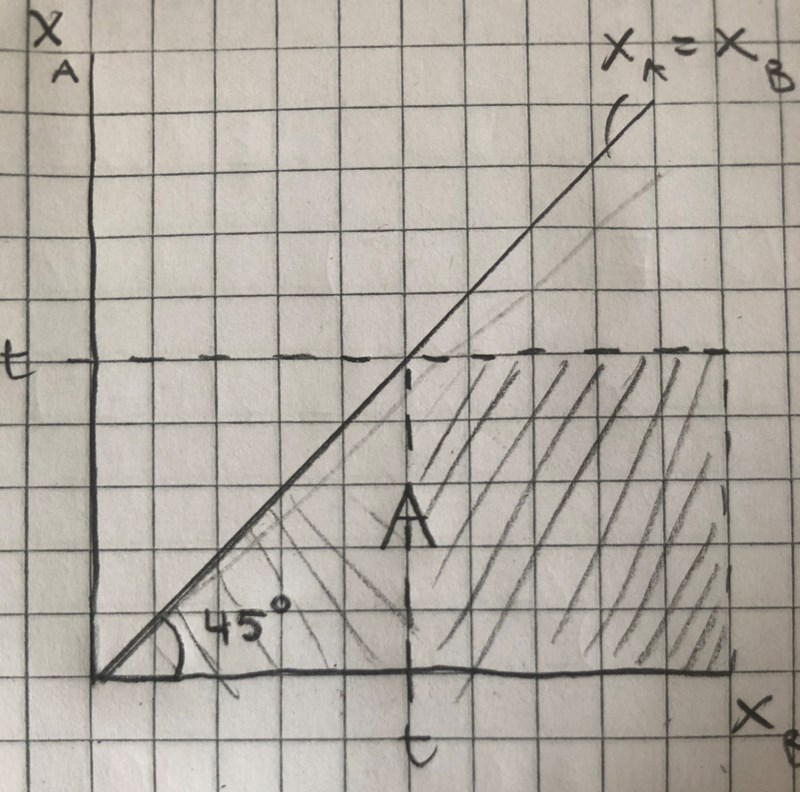
Dela upp området i en triangel och en kvadrat.
Kvadraten: x går från t till 2t, y går från 0 till t.
Triangeln: x går från 0 till y, y går från 0 till t.
Hmm, okej. Vilken borde jag ha först?
Det var egentligen onödigt att dela upp området i två.
Eftersom Området i y-led begränsas av två linjer där y är konstant så är det smidigt att ta y sist.
Först går x från y till 2t.
Sedan går y från 0 till t.
Om jag nu sätter de ovan nämnda gränserna, hur kan då få den dubbelintegralen att resultera i uttrycket . Jag har försökt och försökt, men kan inte få ordning på det.
Fibonacci skrev:Om jag nu sätter de ovan nämnda gränserna, hur kan då få den dubbelintegralen att resultera i uttrycket . Jag har försökt och försökt, men kan inte få ordning på det.
Visa hur du har försökt! Vi som svarar här är bra på matte, men vi klarar inte att hitta var du har gjort fel om vi inte vet exakt hur du har försökt - vi är usla tankeläsare. Meningen med Pluggakuten är att du skall få den hjälp du behöver för att kunna lösa dina uppgifter själv, inte att någon annan skall servera dig färdiga lösningar på dina problem. /moderator
Jag vet att (utan hänsyn till indexering) är en primitiv funktion till och att (återigen utan hänsyn till indexering) är en primitiv funktion till
Det är indexeringen som rör till det för mig tror jag.
Om jag skulle lösa den här uppgiften skulle jag byta ut alla krångliga beteckningar mot sådana som jag begriper. Jag skulle byta ut xA mot x och xB mot y, samt mot A och mot B - detta om de olika är konstanter, annars blir det krångligare. Kan detta vara något för dig också? Eller har jag misstolkat uppgiften totalt?
I så fall har jag också misstolkat uppgiften eftersom jag också har betraktat som en konstant då jag har brutit ut när jag tog fram den primitiva funktionen. Men tack för tipset, jag ska prova.
Får det fortfarande inte att stämma. Jag får att
Kan du lägga in en bild av ursprungsuppgiften, så att vi kan se om vi har tolkat den rätt?
Fibonacci skrev:Får det fortfarande inte att stämma. Jag får att
Det borde inte vara kvar något y efter integreringen. Och jag tycker integralen med x som nedre gräns borde vara den inre, för x borde också försvinna.
Har vridit och vänt på det hur mycket som helst. Är vi helt säkra på integrationsgränserna?
Varför skall man inte integrera som
?
Dvs varför stannar man integrationen vid 2t? Hur kommer man fram till det?
Tyvärr, verkar det ändock inte ge rätt svar, om än snarlikt - får i täljaren. Kanske fel i facit?
Hursomhels, kanske värt att kolla att man verkligen spikat integrationsområdet.
Edit: Ah, men det blir nog rätt. Blandade i hop hur A och B skulle tolkas. B = , så det blir korrekt.
PATENTERAMERA skrev:Varför skall man inte integrera som
?
Dvs varför stannar man integrationen vid 2t? Hur kommer man fram till det?
Tyvärr, verkar det ändock inte ge rätt svar, om än snarlikt - får i täljaren. Kanske fel i facit?
Hursomhels, kanske värt att kolla att man verkligen spikat integrationsområdet.
Edit: Ah, men det blir nog rätt. Blandade i hop hur A och B skulle tolkas. B = , så det blir korrekt.
Snyggt! Har tragglat med den här hur länge som helst. En fråga bara: vad är I i din uträkning?
Fibonacci skrev:Snyggt! Har tragglat med den här hur länge som helst. En fråga bara: vad är I i din uträkning?
Det betyder insättning. Det finns två sätt att skriva detta
, eller
.
Jag brukar använda den förra för att det är lite mindre att skriva, men den senare kanske är lite vanligare i gymnasiet, så du kanske är mer van vid den.
Ah okej, den notationen var ny för mig. Som du skrev, mer van vid den senare. Tack för hjälpen!






