Integrera
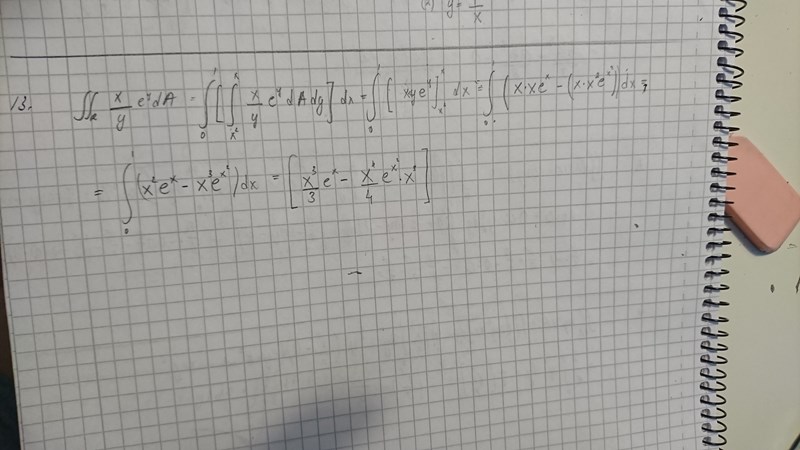
Hur integrerar jag x^3*e^(x^2)
Känns som jag inte alls vet hur jag ska göra..
Sätt och använd partiell integrering.
Har du lust att visa lite närmare hur du menar?
Försök själv! Kör du fast, kommer du att få hjälp, men det är troligen ingen som har lust att servera dig en färdig lösning. Att substituera klarar du säkert. Har du lärt dig partiell integration?
Jodå det kan jag. Men inte på denna. Jag kommer inte alls vidare iom att jag dels inte vet vad jag ska ha som u för att jag ska kunna göra partiell integration på rätt sätt.. Eller ja, det sätt jag vet i alla fall.
Så jag undrar alltså hur ska jag sätta u=x^2 och därefter använda partiell integration? x^3*e^x^2
Om jag då ska sätta u=x^2 hur gör jag med resten? och hur formulerar jag mig då i nästa steg?
Försök göra substitutionen! Eftersom du behöver göra om dx till du så kommer den där hemska trean att försvinna.
Jag har ju ingen aning om hur jag ska göra? Alltså kan jag inte ens försöka för det blir bara tomt efter iom att jag inte förstår hur jag ska gör om jag ska sätta u=x^2.
Där det står skall du sätta in istället. Vad skall göra för att få bort ? (Du har sambandet . Derivera båda sidor. Skriv VL som . Tänk digatt du multiplicerar båda sidor med . Då får du fram vad det är du skall byta ut mot .)
Ja det där vet jag. Men jag vet inte i sammanhanget hur jag ska göra. Alltså vad gör jag rent konkret med x^3 och hur använder jag den "vanliga formeln" när man bryter ut u*v framför integralen i detta fall iom att jag har x^2*e^x innan också. Därav min önskan om att få se hur jag ska gå tillväga. Jag vet principerna men på just denna uppgift får jag det inte att fungera på "vanligt sätt".
Använd sedan partiell integration.
Guggle skrev :Använd sedan partiell integration.
Okej. Men du har ju tagit bort det innan? Det är ju bla det som gör att jag inte riktigt förstår hur jag ska göra..
Vad är det du menar att någon har tagit bort? Det är lite otydligt vad "det" syftar på i ditt inlägg.
Men det så menar jag x^2e^x om står innan - x^3e^x^2
Inget har tagits bort, 1/2dt är xdx och x^2 är t enligt substitutionen.




