integrera & hur kan man se att den har partiell derivate på randen?
Försöker förstå den här integrationen;
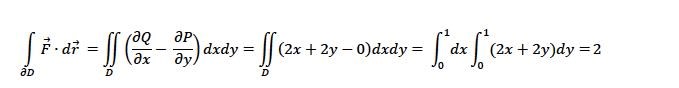
För int dx blir ju x, och int 2xy+y^2 så det borde väl, med gränserna bli 2*1*1+1^2 = 3 ? Inte 2?
-----
samt, hur kan man se att denna

Är paritell på randen?
bump?
Vad menar du med "är partiell på randen?"? Som svar på den första frågan, du vill först integrera med avseende på y (och sätta in gränserna). Då blir du av med y-beroendet och får en funktion av bara x. Sedan vill du integrera den funktionen med avseende på x.
Dvs: .
P och Q är polynom i x och y. Polynom är deriverbara överallt.
Det står att respektive är kontinuerliga i D och på D:s rand och att respektive har kontinuerliga derivator i D och på D:s rand. Det står inte någonstans att någonting skall vara eller är partiell på randen, vad det nu skulle betyda.



