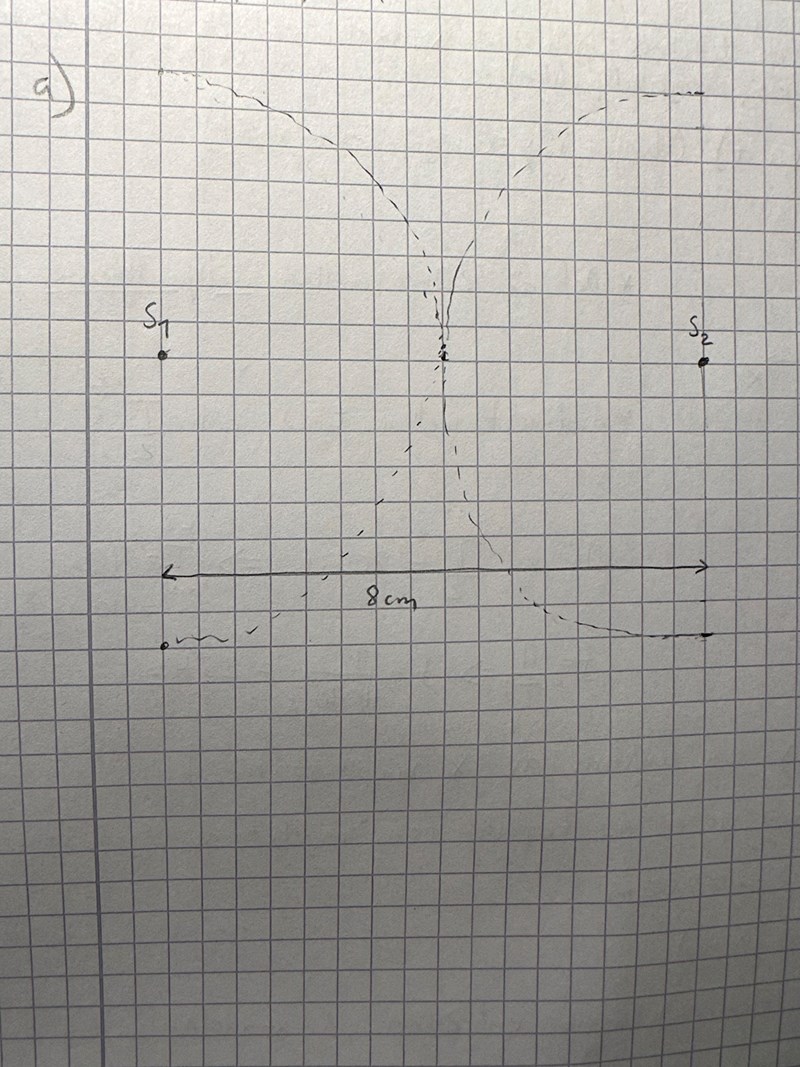
Interferens mekaniska vågor

Vilka punkter finns det mellan S1 och S2 som ligger på avståndet $(p + \frac{1}{2})\lambda$ från S1? Vilka p är möjliga?

Uppgiften nämner att det finns en buk. 

Därav betyder det att det är grundsvängning (n=1), 1 buk och två noder?

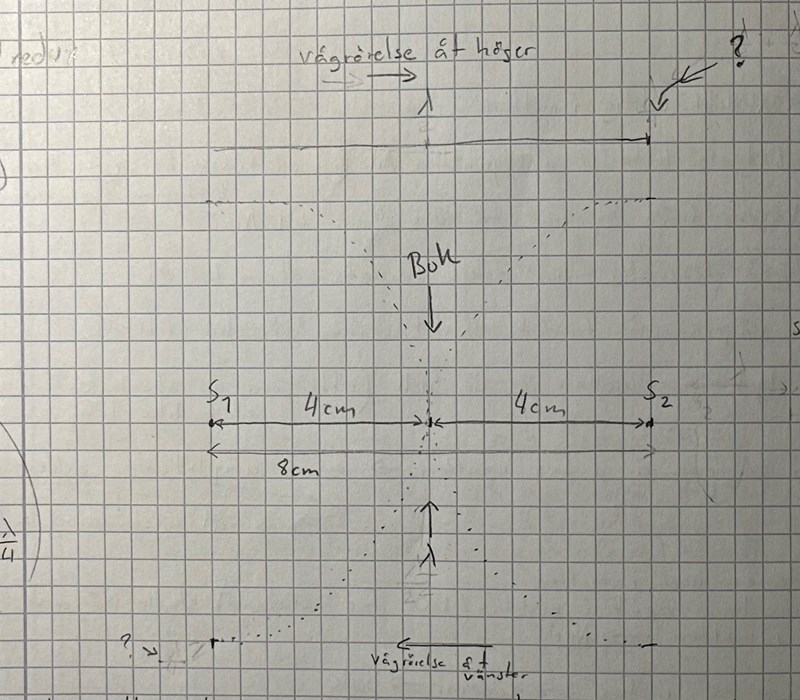
n=p

stämmer min figur?

vart ska noderna vara?

Och vad ska vara vid frågetecknet? Lambda/4 ? Varför isåfall

När skillnaden i väg är ett helt antal våglängder ($∆s = p\lambda$) får man en förstärkning eller buk.

När skillnaden i väg är ($∆s = (p+\frac{1}{2})\lambda$) för man en försvagning eller nod.

Vi har en våg åt höger och en våg (från S2) åt vänster. Till mittpunkten har de båda två 4cm och det är λ, inte λ/2. Där är skillnaden i väg är noll, dvs p=0. Där är alltså en buk.

För att få en nod ska skillnaden i väg vara λ/2, 3λ/2, 5λ/2,....

jag hänger inte riktig med.

om mitten är en buk och motsvarar en λ så betyder detta vågkällorna startar ifrån varsin buk 

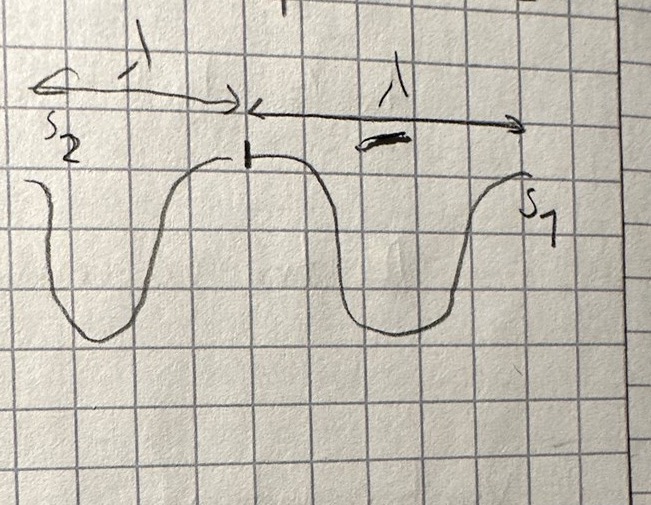
Noder och bukar är en beskriver interferensmönstret, inte vågorna i sig.
När två vågor med samma våglängd möts skapas ett mönster där vissa punkter rör sig mer än med bara en våg och andra står stilla hela tiden.

Ett försök att beskriva det i bild:

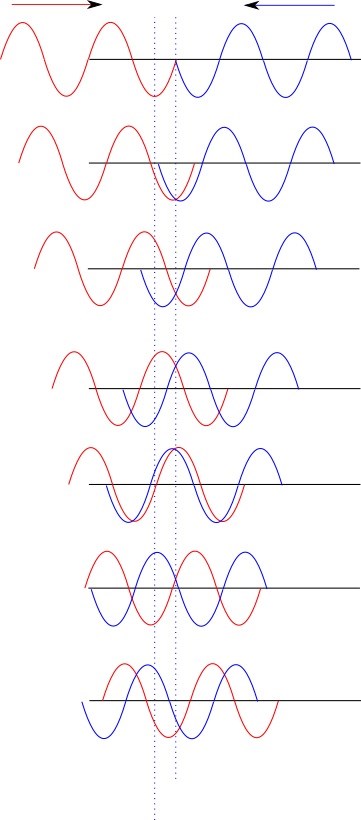
Se dessa som blixtfoton tagna med jämna mellanrum. I första bilden har vågorna precis mötts.

Om du tittar på den högra streckade linjen så ser du att vågorna går alltid åt samma håll, de förstärker varandra. Vid en vänstra streckade linjen går vågorna alltid åt olika håll, de släcker ut varandra.

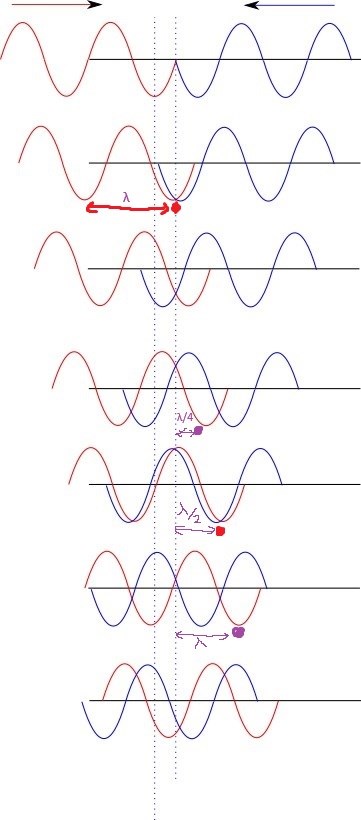
de jag är ute efter är noderna, dvs de punkter där de släcker ut varandra?

kan man anta mönstret för noder är varje λ/4 från en buk (S1)? man adderar sig fram ?

Det gäller att se om vägskillnaden uppfyller formeln som gäller för noder.

Hur långt är avståndet från S1 till en punkt, hur långt är avståndet från S2 till samma punkt ? Uppfyller skillnaden, mätt i våglängder, mellan avstånden formeln?

i facit står det 1 cm, 3 cm, 5 cm, 7 cm. Vägskillnaden från S1 till S2 ska vara en halv våglängd

ska man pröva sig fram med λ/2, 3λ/2, 5λ/2,

till 1:a minimi så är det λ/2,

och till den 2:a minimi så är det (λ/2)+λ = 3λ/2

och i den 3:e minimi så är det (3λ/2) + λ = 5λ/2.

vid 4:e minimi så är det (5λ/2)+λ =7λ/2

man går om 1λ till bråkform för varje beräkning, för att får gemensamma nämnare

Vägskillnaden från S1 till S2 ska vara en halv våglängd

Njae, det avståndet är ju 8cm.
Vi ska hitta punkter mellan S1 och S2 där vägskillnaden mellan S1P1 och S2P1 är $(p +1/2)\lambda$. T.ex den här punkten.

Vägskillnaden blir då $\frac{7}{4}\lambda - \frac{1}{4}\lambda = \frac{6}{4}\lambda = \frac{3}{2}\lambda$

Sen frågas det efter avståndet mellan dessa punkter och S1. I detta fallet $\frac{1}{4}\lambda = 1cm$