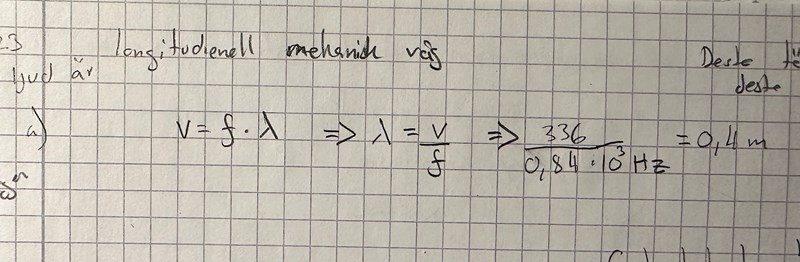Interferens ljud
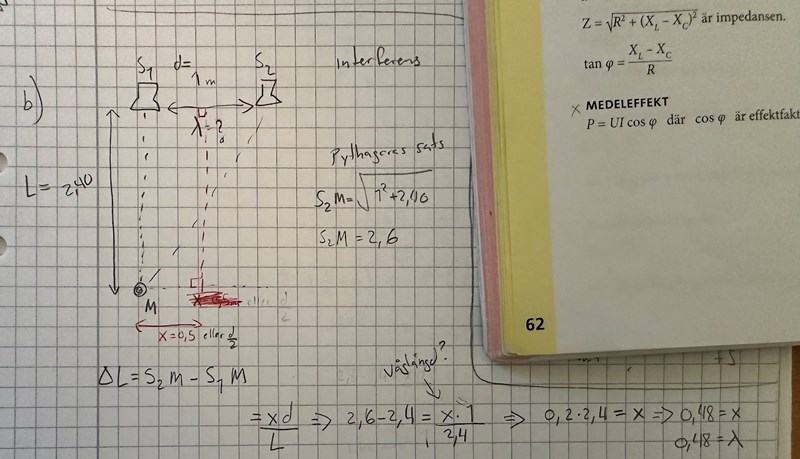


Hejsan jag har fastnat på b)
svaret ska bli lambda/2
Det ser ut som om du är på rätt väg med vägskillnaden.
Vad fick du våglängden till?
Sedan är svaret på (b) bara en division bort. Exempel: vägskillnad 10 m och våglängd 2 m. Då går det 5 våglängder på den vägskillnaden.
Biorr skrev:
Stämmer bra!
Så våglängden är λ=0,4 m och du fick vägskillnaden till 2,6-2,4 m.
Vad är då vägskillnaden uttryckt i λ?
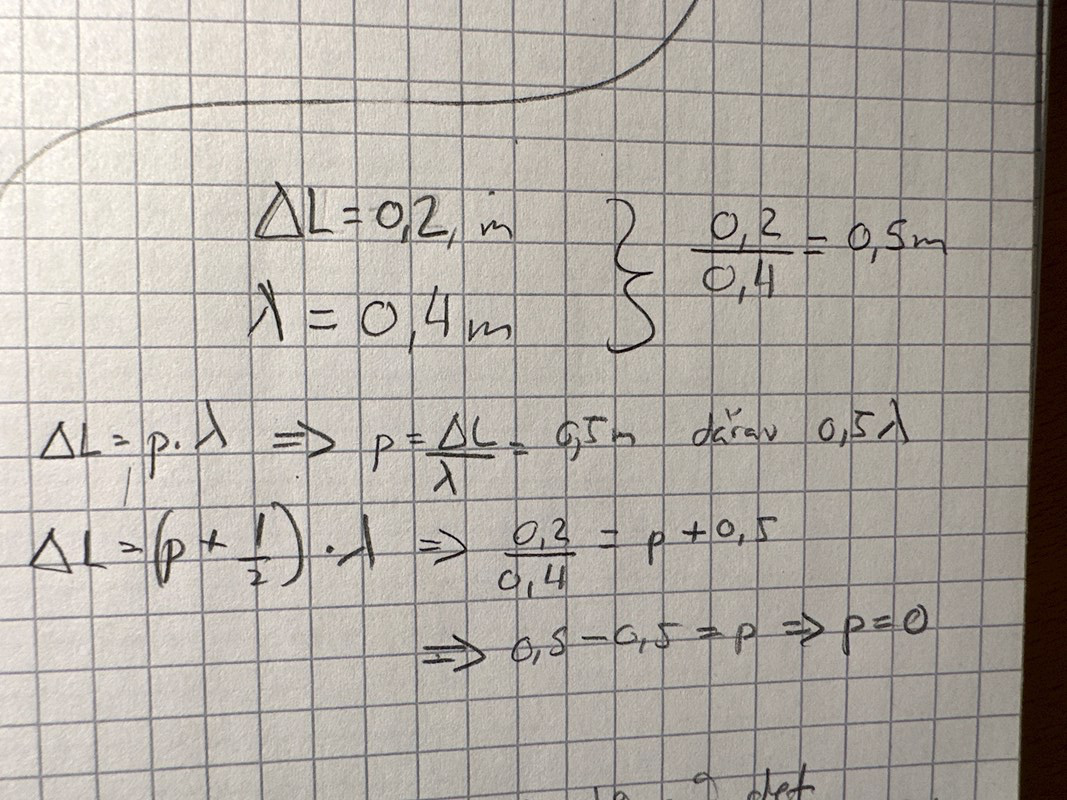 Hur kan man anta att det är en konstruktiv interferens?
Hur kan man anta att det är en konstruktiv interferens?
Biorr skrev:
Hur kan man anta att det är en konstruktiv interferens?
Nej, det skall man inte anta. Det är en destruktiv interferens.
Kikar man i formelbladet du klippt in så har du ett alternativ där vägskillnaden är (p+1/2) våglängd, för p=0, 1, 2, ... (Någon har skrivit dit "udda", men det skall suddas. Det gäller för alla heltal.)
I det här fallet är p=0 och vi har en halv våglängds vägskillnad, vilket ger en försvagning i punkten M.

Sedan skall jag vara lite petig. Vägskillnaden och våglängden har båda enheterna meter. När du räknar ut "0,5" nedan så är detta värde enhetslöst. Det betyder "en halv" (våglängd). Inga meter där.
Så här låter det i punkten M när båda högtalarna är igång:
Högtalare S1 (rött) och S2 (blått), där S2 ligger en halv våglängd efter.
Summan av dessa ljudvågor ser du i M (grönt). De är en halv våglängd (180 grader, eller pi radianer) ur fas och släcker ut varandra.
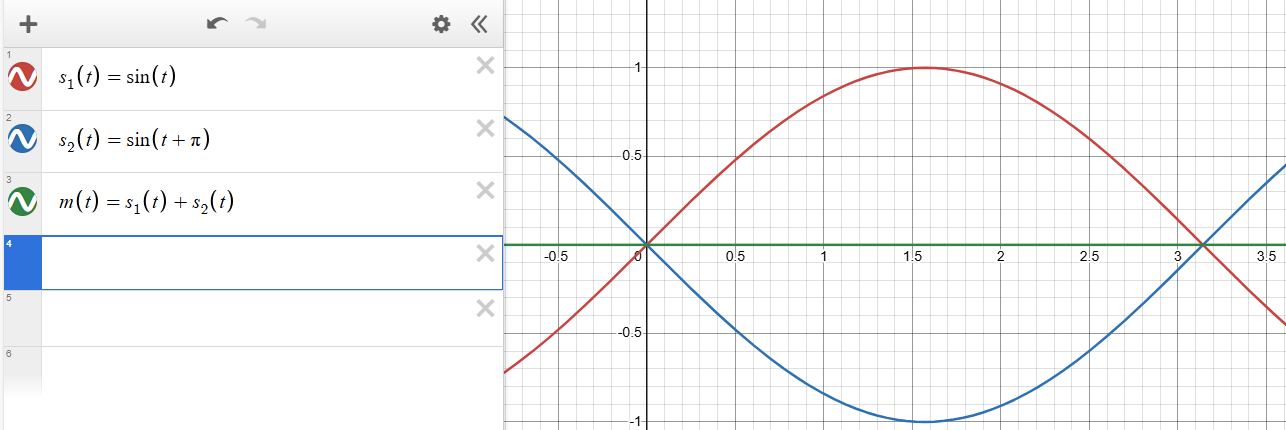
Då är det inte så svårt att besvara sista frågan, alltså om ljudstyrkan ökar eller minskar i M när S2 slutar fungera.
Om b) är en destruktiv interferens så skulle det På c) vara att vid destruktiv interferens så tar vågorna ut varandra. Därav skulle figuren visa en rak horisontellt linje.
om högtalare 2 slutar fungera så kommer ljudet av högtalare 1 öka. Figuren skulle visa en vanlig sinuskurva.
men jag tänker hur vet jag vilken formeln jag ska använda? Jag vet bara att vi en sinuskurva så är vågtoppen förstärkning och noderna på x-axeln är försvagningar.
i försvagningar är det p=0 då blir det lambda/2
p=0 betyder att?
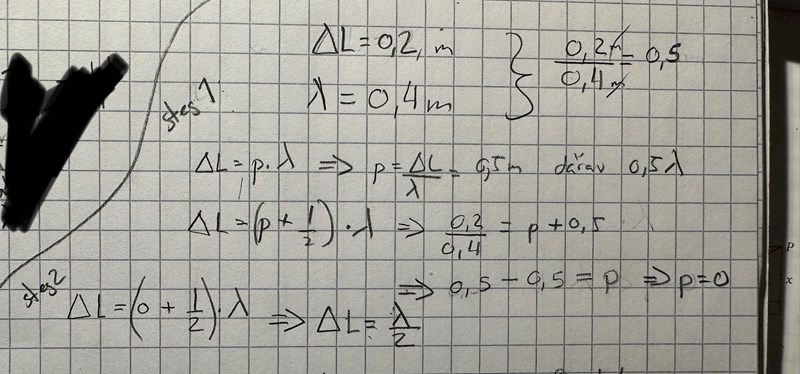
Det formelbladet säger är att du har konstruktiv interferens när vägskillnaden är 0, 1, 2, … våglängder.
Du har destruktiv när den är 0,5, 1,5, 2,5, … våglängder.
0, 1, 2, … är ditt p.
I verkligheten skall det dock mycket till för att vågorna skall släcka ut varandra helt. Det är en (matematisk) punkt vi talar om. Inte ens ditt öra är en punkt och dessutom finns det troligen saker i omgivningen som reflekterar ljudet.
Just ja.
På bilden där jag skrivit ”udda” inlägg 1
jag menade jag troligen att ett värde på P (heltal) som leder till att ΔL =0,5λ så är det ett udda tal, så tyder det på att punkten M är en minimipunkt (försvagning).
Likaså om ett värde på P (heltal) som leder till att ΔL =1λ så är det ett heltal, så tyder det på att punkten M är en maximipunkt (förstärkning).
så först beräknar jag p, och sedan genom att sätta p=0 i vardera formel, så kan jag avgöra om punkten M är minimi eller maximipunkt.
Snyggt!
Udda tal är dock 1, 3, 5 … Tror du tänker på decimaltal, alltså tal som inte är heltal. Eller fattar jag fel?
jo, borde nog säga decimaltal
Alt 2. Din metod var snabbare för att ta reda på om det var hela våglängder
eller
våglängder i decimaltal
och utifrån det avgöra om en punkt är maximi eller minimipunkt