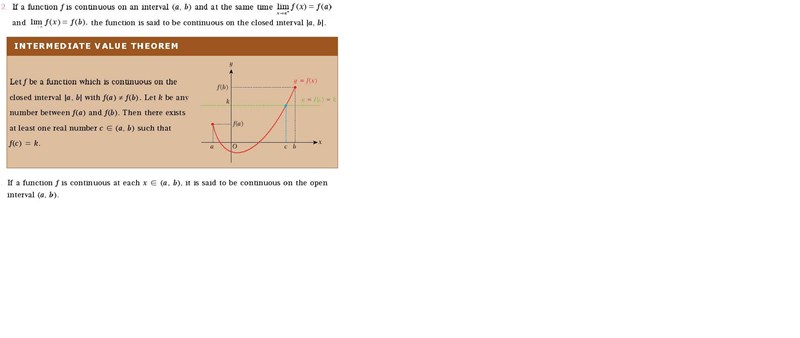
intermediate value theorem
jag undrar varför måste f countinuous on the closed interval [a,b] och inte open in terval (a,b)
Den måste vara kontinuerlig på det stängda intervallet [a,b] eftersom det annars går att skapa "hopp" i funktionen som gör att satsen inte gäller.
Tänk ex. om du skulle ha f(x)=x på det öppna intervallet (0,1) men du låter f(0)=100 och f(1)=-100. Då finns det en massa tal k mellan f(0) och f(1) som funktionen aldrig kan anta på (0,1). Finns säkert riktiga bevis men detta förklarar principen.
Den behöver vara kontinuerlig på ett stängt intervall och inte ett öppet intervall på grund av anledningen att ett öppet intervall saknar ändpunkter och det går därför inte att beräkna funktionens värde i ändpunkterna.
Tänk dig att du har funktionen f(x)=x som är kontinuerlig för alla x men är endast definierad för intervallet x=(0,10]. Vad är funktionens minsta värde?

