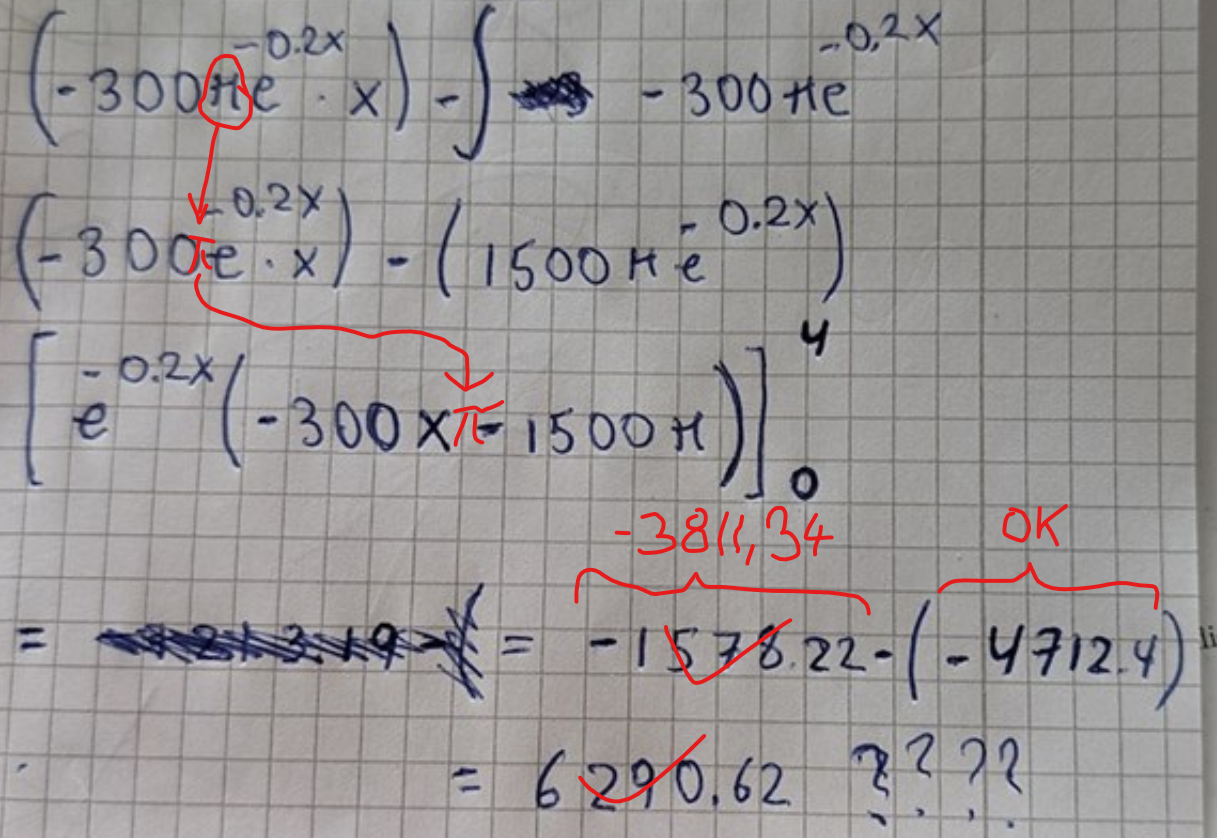Invånare i stad, radie
Hej,
Jag undrar hur man hittar primitiva funktionen till den här integralen. Verkar vara svårt för värdena jag får är långt ifrån korrekt svar..
Fråga 3477 c)

.
.
Såhär tyckte jag då
Använd partiell integration. Sätt .
Det har jag aldrig sett förut, får pröva det lite senare 🙂 tack
Dkcre skrev:Det har jag aldrig sett förut, får pröva det lite senare 🙂 tack
Ja, det passar väldigt bra när man har en exponentialfunktion för den är enkel att integrera och kan man då "derivera bort" den andra funktionen så är man "hemma".
Lite mer information här:
http://wiki.sommarmatte.se/wikis/sommarmatte2/index.php/2.3_Partiell_integrering
Men man måste inte använda den metoden utan det ska funka som jag giort, ändå, frågan är vad jag gör fel?
Gjorde sådär nu, och får ändå fel svar. Kan inte se något fel.
Dkcre skrev:Men man måste inte använda den metoden utan det ska funka som jag giort, ändå, frågan är vad jag gör fel?
Med din ovan använda metod, vad är primitiv funktion till
x * x
?
(x^3)/3
Dkcre skrev:(x^3)/3
Det stämmer, men med den metod du använder här
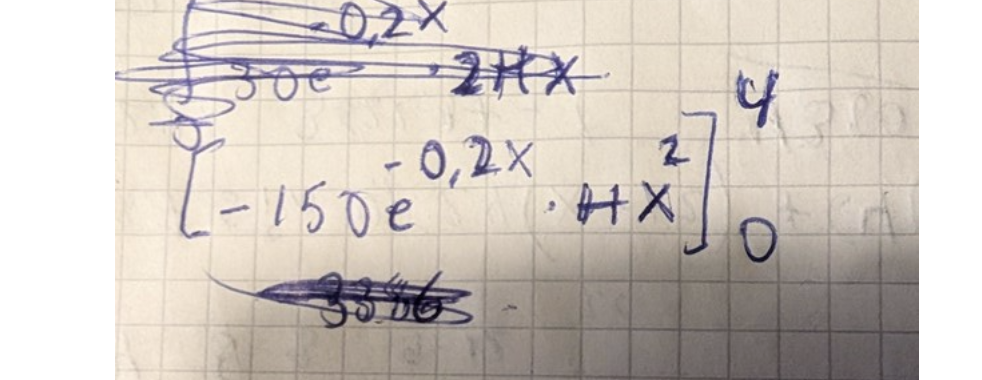
så skulle de bli
x^2/2 * x^2/2 = x^4/4
Vi inser härmed att din metod är felaktig.
Ja, jag har vetat att den vart fel hela tiden.
Så man ska multiplicera ihop funktionerna först och sedan ta primitiva funktionen eller vadå? Finns ingen förklaring hur man ska göra i boken och i vanlig ordning fattar jag inte. Har multiplicerat ihop dem tidigare också och prövat men det blev säkert fel.
Blir kanske -300πe^(-0.2x) x^(2) då.
Dkcre skrev:Ja, jag har vetat att den vart fel hela tiden.
Så man ska multiplicera ihop funktionerna först och sedan ta primitiva funktionen eller vadå? Finns ingen förklaring hur man ska göra i boken och i vanlig ordning fattar jag inte. Har multiplicerat ihop dem tidigare också och prövat men det blev säkert fel.
Blir kanske -300πe^(-0.2x) x^(2) då.
Om du ska lösa den algebraiskt måste du använda formeln för partiell integration. Alternativet är numerisk lösning, men känns inte som det är tillåtet här.
Tror integralen ska lösas med räknare då ingen av dessa metoder tas upp. Framgår ej naturligtvis. Men nu måste jag göra det såhär.
Har försökt här men det är fortfarande fel med någonting..
Jag läste lite om partiell integration också och det står att det kan användas för att underlätta, men i vissa fall blir det svårare och man är better off att lösa det med, ja, standardutförande. Hur vet jag om det inte går att lösa utan den metoden som det tydligen är i detta fall?

Med lite erfarenhet kan man ansätta (Ax+B)enånting, och se vad dess derivata blir.
Okej.
Denna uppgift finns även i den nyare boken Matematik 5000+, kurs 4. I den boken är deluppgiften (c) tydligt markerad att man förväntas använda sig av en miniräknare (eller ett annat digitalt verktyg).
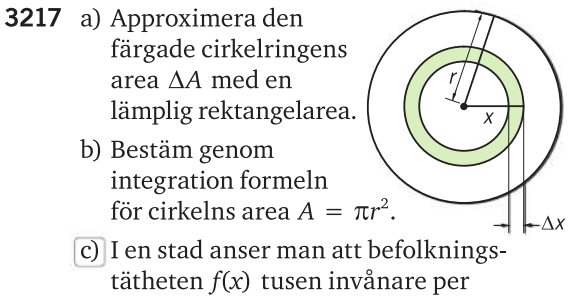
Partiell integration tas inte alls upp i denna bok, den kommer först i Matematik 5000+kurs 5. Ansatsmetoden som föreslagits i #12 tas inte heller upp i boken. (Å andra sidan har uppgiften klassificerats som nivå 3, så man måhända kan klura ut på egen hand vilken ansats som är lämplig.)
Varför är man intresserad av en ansats? Vad spelar det för roll förutom att det ser lite snyggare ut?
Vad missförstår jag i #11? :/
Jo, det är nivå 3. Känner att det nästan alltid är alldeles för svårt för mig. Tillåter dock inte att inte göra dem i alla fall..
Tack. :)
Ser snyggare ut än vad? Det är ett alternativ till partiell integration, och eventuellt har man sett sådana ansatser innan man har lärt sig partiell integration.
Har gjort det exakt enligt formeln för partiell integration flertalet gånger men det stämmer inte. Klarar inte av det. Skitsamma.
Visa gärna igen hur du har tänkt!
Jag kan inte se att det blir någonting annat än i svar #11. Det jag vet att jag inte gör är att jag inte flyttar ut k = 60π från integralen, men tänker att det inte gör någonting om man arbetar med den heller. Eller så måste man ta ut den?
Visar imorgon hur som helst. Godnatt 👌
Om du låter vara en konstant innanför eller utanför integralen ska inte spela någon roll. Jag ska kika lite noggrannare på #11. Godnatt!
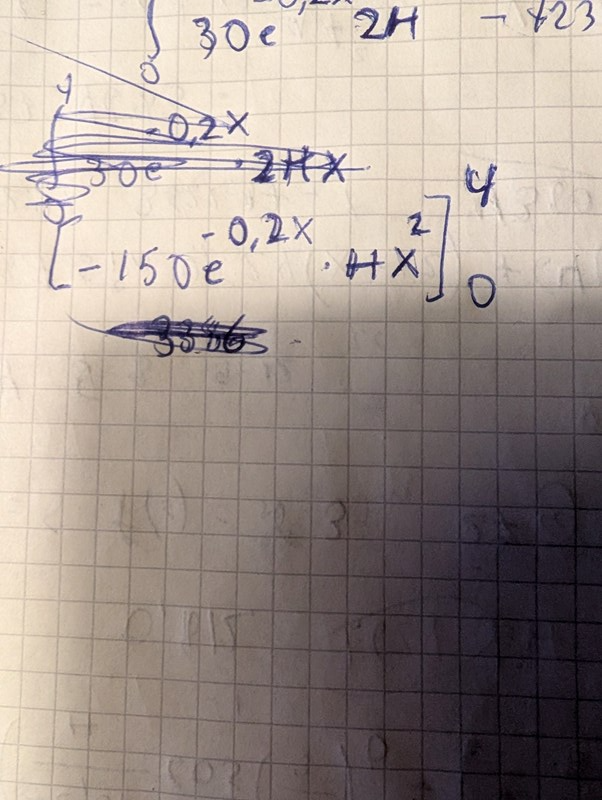
Såhär blev det nu, gjorde om fr.o.m steget när jag flyttade ut e^(-0.2x) uttrycket på papperet nedan.

Tack så mycket. Det jag missade att göra, bortsett från slarvfelen där, var att jag behandlade varje uttryck i integralen var för sig, dvs första uttrycket fick stå för x=4 och andra för x=0. Men det är ju x=4 för båda termer i uttrycket subtraherat med x=0 i andra.
Tyckte inte det framgick alls i exemplet för partiell integration där. Fast det var väl underförstått antar jag..
Men nu kan jag äntligen gå vidare och göra något mer produktivt.
👍