Invers Fouriertransform

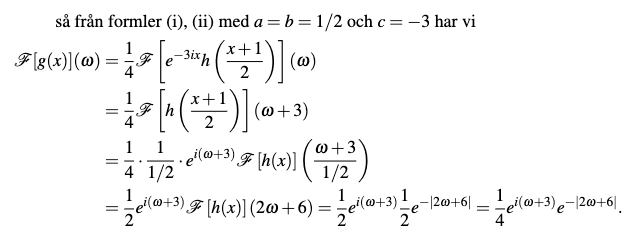
Uppgift c) handlar om att beräkna Fouriertransformen av ett uttryck som blir lite tråkigt att integrera. Dessutom är man ofta lat av sig och vill återanvända det man gjort tidigare om det går snabbare och enklare. Därför använder man i facit resultatet från den tidigare beräkningen samt lite specialregler.

Vanligtvis ingår grundläggande uttryck i en formelsamling (se till exempel Beta) 

$\displaystyle f\left(x\right)=\frac{1}{x^2+a^2},\quad f\left(t\right) \xrightarrow{\mathcal{F}} F\left(\omega\right),\quad F\left(\omega\right)=\frac{1}{2a}e^{-a|\omega|}$

Med den formeln samt med förskjutningsreglerna är det enkelt att beräkna din transform. Förskjutningsreglerna kan till exempel formuleras så här:

$\displaystyle f\left(x-a\right)\, \xrightarrow{\mathcal{F}}\, e^{-i\omega a}F\left(\omega\right),\quad e^{i\Omega x}f\left(x\right)\, \xrightarrow{\mathcal{F}}\, F\left(\omega-\Omega\right)$

Om man inte har tillgång till en formelsamling kan man göra som i facit och utnyttja vad man gjort tidigare för att spara tid och energi.

Funktionen $h\left(\omega\right)=\frac{1}{1+\omega^2}$ är ju nästan vad vad du fick som svar i uppgift b). Det är just därför man väljer den som $h\left(x\right)$. 

I uppgift b) har du alltså embryot till en egen formelsamling, med en funktion och dess Fouriertransform. När man har en Fouriertransform till en funktion är det enkelt att i sin tur hitta denna funktions  transformation (som om transformen hade varit en funktion i $x$) och facit visar hur man kan göra det med manipulation. 

Är du med?

Det visar sig sig att knepet kan förkortas till att helt sonika sätta in $-\omega$ istället för $x$ och dela med $2\pi$ (eftersom ni använder den varianten av transformen) för att hitta den "nya" transformen. Det här blir lätt lite förvirrande men ungefär så här:

   $\phi=\hat{f} \rightarrow  \hat{\phi}=\frac{1}{2\pi}f\left(-\omega\right)$

Om ni inte har lärt er det är det kanske bättre att du fortsätter göra som i facit.

Vi har inte tillgång till en formelsamling med grundläggande uttryck som du nämnde. Men samtidigt förstår jag inte vad facit gör. Skulle önska en förklaring av facits lösning, under förutsättning att jag inte har tillgång till någon formelsamling

Det första facit gör är att skapa en Fouriertransform till funktionen $h\left(x\right)=\frac{1}{1+x^2}$

$\hat{h}\left(\omega\right)=\mathcal{F}\left[h\left(x\right)\right](\omega)=\mathcal{F}\left[\frac{1}{1+x^2}\right]\left(\omega\right)$ 

Varför vill facit skapa just den Fouriertransformen? Jo, för det första finns en snarlik funktion med i uppgift c, i formen $\frac{1}{(x+1)^2+4}$, för det andra är det samma funktion som du kommit fram till i uppgift b, dvs $\frac{1}{\omega^2+1}$. När man har utfört transformationen av en funktion är det enkelt att gå "baklänges" till ursprungsfunktionen. Och det är exakt det vi ska göra nu! Vi vill alltså beräkna Fouriertransformen till funktionen $h\left(x\right)$

$\displaystyle \hat{h}\left(\omega\right)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\frac{1}{1+x^2}e^{-i\omega x}\,\mathrm{d}x$ (1)

Det första vi gör är att använda formeln för invers Fouriertransform tillsammans med vad du kom fram till i uppgift b). Vi ställer upp

$\displaystyle e^{-|x|}=\int_{-\infty}^{\infty} \frac{1}{\pi(1+\omega^2)} e^{i\omega x}\,\mathrm{d}\omega$

Nu ska vi manipulera ekvationen. Eftersom funktionen är jämn får vi byta ut $x$ mot $-x$ överallt utan att det påverkar integralens värde det minsta. Vi passar också på att flytta ut konstanten $\frac{1}{\pi}$ utanför integralen

$\displaystyle e^{-|x|}=\frac{1}{\pi}\int_{-\infty}^{\infty}\frac{1}{(1+\omega^2)} e^{-i\omega x}\,\mathrm{d}\omega$

Nu byter vi namn på variablerna så att $\omega$ blir $x$ och $x$ blir $\omega$. Vi passar också på att dela båda sidor med 2.

$\displaystyle\frac12e^{-|\omega|}=\frac{1}{2\pi}\int_{-\infty}^{\infty}\frac{1}{(1+x^2)} e^{-i\omega x}\,\mathrm{d}x$

Notera att detta är exakt samma uttryck (1) som vi söker för $\hat{h}\left(\omega\right)$ ! Vi har därmed etablerat att

$\displaystyle \mathcal{F}\left[\frac{1}{1+x^2}\right]\left(\omega\right)=\frac12 e^{-|\omega|}$

Är du med så långt? Om inte, förklara vilket steg du inte förstår.

Nu förstår jag mycket bättre. Tusen tack!