Inverse funktioner
Frågan lyder, se bild:
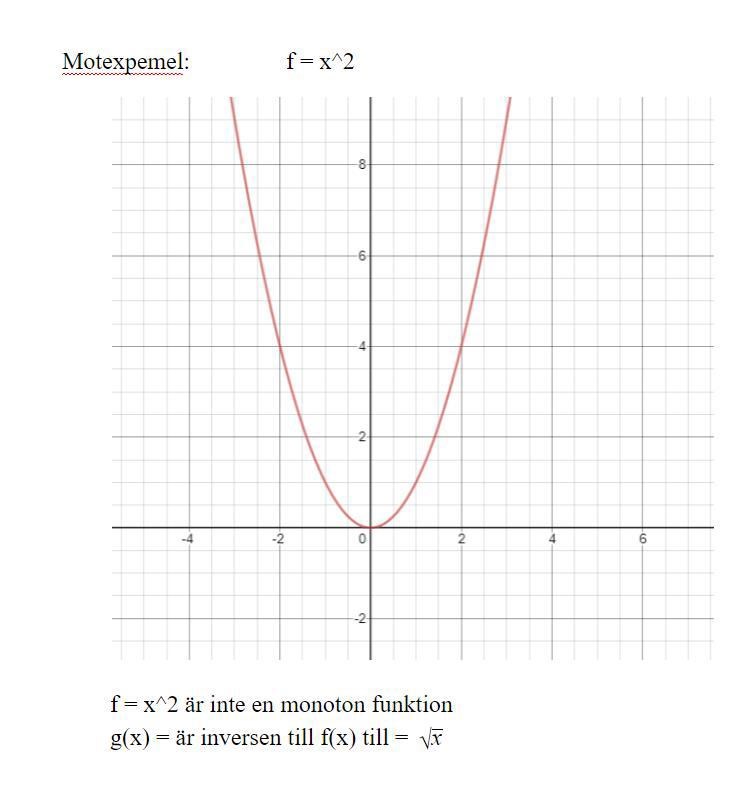
Min lösning:
Har jag tänkt rätt eller är jag ute och cyklar?
f(x) = , x ≥ 0, är strängt monoton.
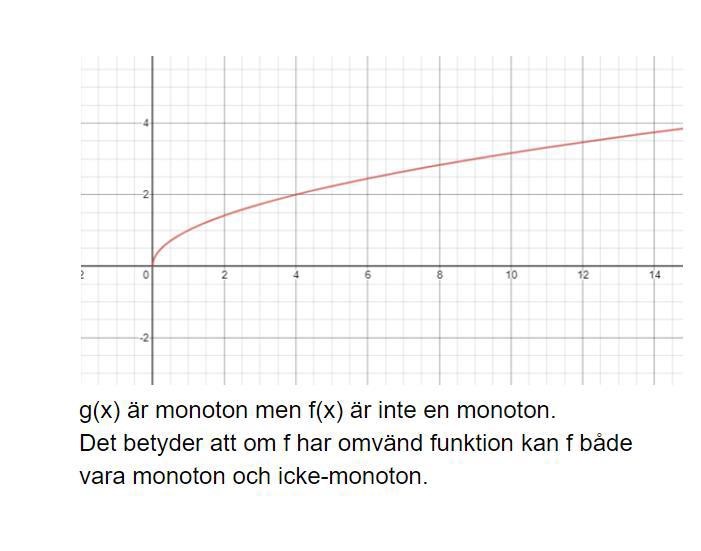
Det är till den som g(x) = , x ≥ 0, är invers.
En strängt monoton funktion är alltid injektiv (ett-till-ett) och har en vänsterinvers, men behöver inte ha en invers.
En funktion med invers är alltid både injektiv och surjektiv (på).
Exemplet du gav är inte så bra för det är inte en injektiv funktion, och inte heller surjektiv.
Nja, du tänker tyvärr fel.
Funktionen är inverterbar endast om du väljer definitionsmängden till att vara (om du har med de negativa talen är funktionen inte injektiv och därmed inte inverterbar). På intervallet är den även strängt monoton, så detta är tyvärr inte ett motexempel till påståendet.
Min spontana tanke (som inte nödvändigtvis är korrekt) är att det inte duger med kontinuerliga funktioner för att hitta ett motexempel. Jag tror du måste kika på diskontinuerliga funktioner.
AlvinB, det går väl också att välja definitionsmängden []?
tomast80 skrev:AlvinB, det går väl också att välja definitionsmängden []?
Helt riktigt. Det går ju också att välja , men samma sak händer där. I det intervallet en invers existerar är funktionen också strängt monoton. Min något slarvigt uttryckta poäng var att hur man än väljer definitionsmängden till kommer det aldrig att bli ett motexempel till påståendet.
Jag tror att AlvinB:s tips om att titta på diskontinuerliga funktioner är värt att tas på allvar.
Tack för svaren! Tips på hur jag kan gå tillväga för att lösa den?
JrCrispy skrev:Tack för svaren! Tips på hur jag kan gå tillväga för att lösa den?
Tänk dig en funktion vars graf är växande i ett första intervall för att sedan göra ett diskret hopp uppåt för att sedan vara avtagande i ett påföljande intervall, utan att komma för lågt förstås.
Kommer du vidare?
Nästan.
JrCrispy skrev:Nästan.
Sov på saken så löser det sig.
Vi kanske skall tydliggöra vad de olika begreppen faktiskt innebär. Att en funktion är inverterbar innebär att det går att finna en invers till funktionen, d.v.s. om går det att finna en invers funktion som går tillbaka, d.v.s. . När kan man då finna en invers? Det hänger på två saker:
- Injektivitet. Det får inte finnas två -värden som funktionen ger samma -värde för. Om det skulle finnas olika -värden för ett -värde är det omöjligt att veta vilket av -värdena den inversa funktionen skall ge när man stoppar in -värdet. Det blir därför omöjligt att konstruera en invers om funktionen inte är injektiv.
- Surjektivitet. Det får inte finnas -värden som funktionen inte ger för något -värde. Om det fanns -värden utan motsvarande -värden blir det ju omöjligt för en invers att länka alla -värden med ett -värde. Detta är något som vi dock inte behöver oroa oss för när vi själva får konstruera funktionen. Då får vi nämligen välja målmängd, d.v.s. välja vilka -värdena är. Då kan vi bara välja målmängden så att funktionen blir surjektiv.
När vi skall konstruera en inverterbar funktion behöver vi främst bry oss om att vår funktion är injektiv. Det kan hjälpa oss att tänka grafiskt. Grafiskt innebär injektivitet att om vi drar en vågrät linje var som helst i koordinatsystemet får den endast nudda grafen en gång. Till exempel är följande funktion inte injektiv eftersom vi kan dra en vågrät linje som skär tre punkter på grafen:
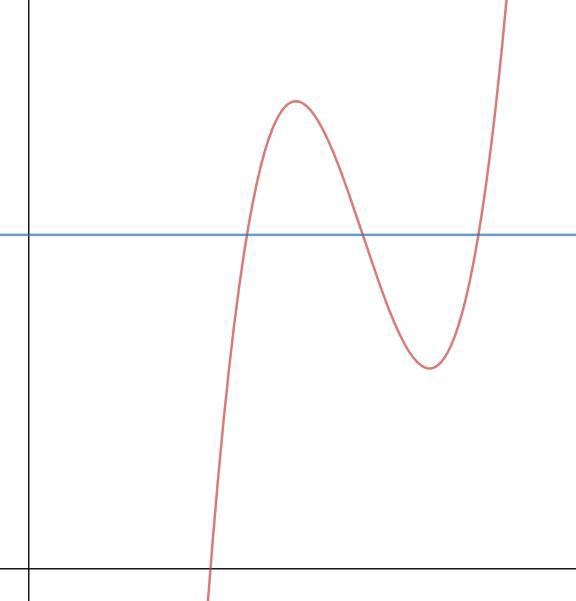
Men följande funktion är injektiv eftersom det inte går att rita en vågrät linje som nuddar grafen mer än en gång:

Vad innebär det då att en funktion är strängt monoton? Jo, formellt sett innebär det att om vi väljer två -värden och sådana att måste det antingen gälla att (funktionen är strängt växande) eller (funktionen är strängt växande) för alla och man väljer.
I praktiken innebär detta att funktionens värden antingen blir större och större ju större blir eller mindre och mindre ju större blir. Man får alltså inte ha en funktion som först växer på något intervall och sedan minskar på något annat intervall. Då är funktionen inte strängt monoton.
Hur ser detta ut grafiskt? Jo, en monoton funktion måste "peka uppåt" eller "peka nedåt" i hela dess graf. Det får inte gå att på ett ställe rita en tangentlinje med positiv lutning och på ett annat ställe rita en tangentlinje med negativ lutning. Vi kan faktiskt ta samma exempel som förut. Följande funktion är inte monoton eftersom det går att finna tangentlinjer med negativ lutning och tangentlinjer med positiv lutning:
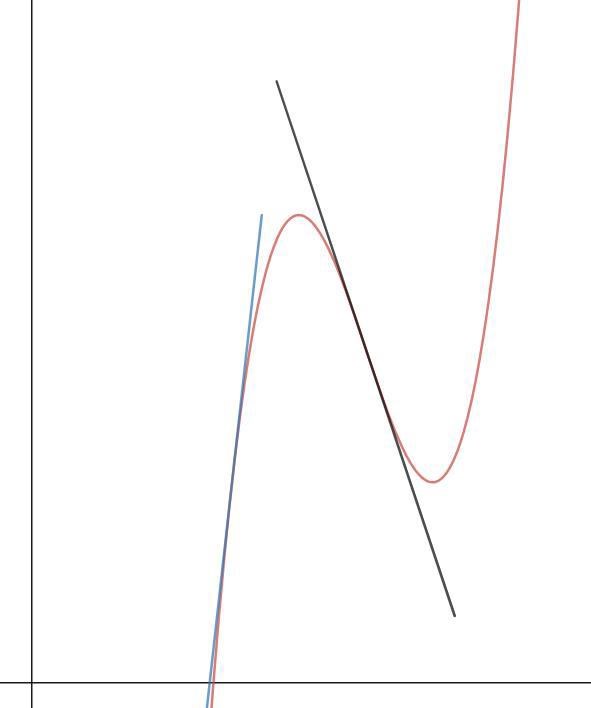
Följande funktion är monoton eftersom den "lutar uppåt" överallt:

För våra exempel gällde det alltså att den inverterbara funktionen var strängt monoton och den icke inverterbara funktionen inte var strängt monoton. Och detta är något som gäller för alla kontinuerliga funktioner (funktioner med sammanhängande grafer som går att rita utan att lyfta pennan). Är en kontinuerlig funktion inverterbar är den också strängt monoton.
Varför gäller då detta? Jo, om en kontinuerlig funktion skall vända nedåt utan att vi får några hopp i grafen måste det ju bildas en slags "bergstopp" () i grafen, och genom den "bergstoppen" kan vi dra en vågrät linje som skär två punkter. Därför kan en kontinuerlig funktion inte vara inverterbar utan att också vara strängt monoton.
Men om vi stryker det där med att funktionen skall vara kontinuerlig behöver vi inte nödvändigtvis få en bergstopp när vi vänder nedåt. Kika exempelvis på följande funktion:
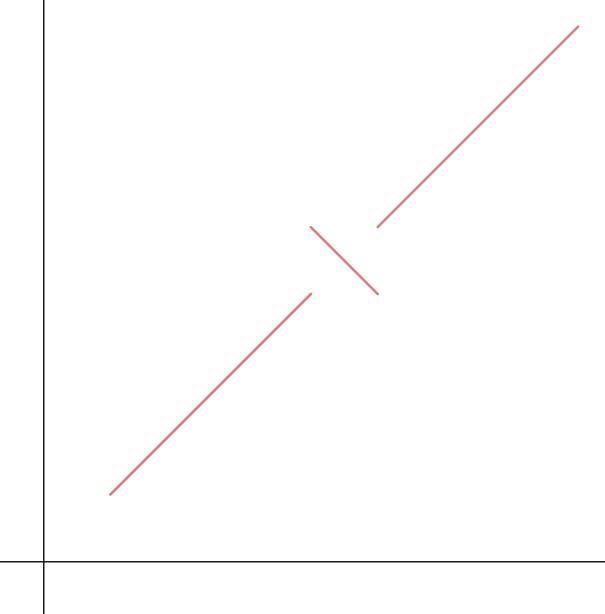
Här kan vi få grafen att tillfälligt peka nedåt utan att bilda en "bergstopp" just för att vi kan göra ett hopp i grafen. Denna funktion är alltså inte kontinuerlig.
Hjälper detta för att ta fram ett motexempel?
AlvinB skrev:Vi kanske skall tydliggöra vad de olika begreppen faktiskt innebär. Att en funktion är inverterbar innebär att det går att finna en invers till funktionen, d.v.s. om går det att finna en invers funktion som går tillbaka, d.v.s. . När kan man då finna en invers? Det hänger på två saker:
- Injektivitet. Det får inte finnas två -värden som funktionen ger samma -värde för. Om det skulle finnas olika -värden för ett -värde är det omöjligt att veta vilket av -värdena den inversa funktionen skall ge när man stoppar in -värdet. Det blir därför omöjligt att konstruera en invers om funktionen inte är injektiv.
- Surjektivitet. Det får inte finnas -värden som funktionen inte ger för något -värde. Om det fanns -värden utan motsvarande -värden blir det ju omöjligt för en invers att länka alla -värden med ett -värde. Detta är något som vi dock inte behöver oroa oss för när vi själva får konstruera funktionen. Då får vi nämligen välja målmängd, d.v.s. välja vilka -värdena är. Då kan vi bara välja målmängden så att funktionen blir surjektiv.
När vi skall konstruera en inverterbar funktion behöver vi främst bry oss om att vår funktion är injektiv. Det kan hjälpa oss att tänka grafiskt. Grafiskt innebär injektivitet att om vi drar en vågrät linje var som helst i koordinatsystemet får den endast nudda grafen en gång. Till exempel är följande funktion inte injektiv eftersom vi kan dra en vågrät linje som skär tre punkter på grafen:
Men följande funktion är injektiv eftersom det inte går att rita en vågrät linje som nuddar grafen mer än en gång:
Vad innebär det då att en funktion är strängt monoton? Jo, formellt sett innebär det att om vi väljer två -värden och sådana att måste det antingen gälla att (funktionen är strängt växande) eller (funktionen är strängt växande) för alla och man väljer.
I praktiken innebär detta att funktionens värden antingen blir större och större ju större blir eller mindre och mindre ju större blir. Man får alltså inte ha en funktion som först växer på något intervall och sedan minskar på något annat intervall. Då är funktionen inte strängt monoton.
Hur ser detta ut grafiskt? Jo, en monoton funktion måste "peka uppåt" eller "peka nedåt" i hela dess graf. Det får inte gå att på ett ställe rita en tangentlinje med positiv lutning och på ett annat ställe rita en tangentlinje med negativ lutning. Vi kan faktiskt ta samma exempel som förut. Följande funktion är inte monoton eftersom det går att finna tangentlinjer med negativ lutning och tangentlinjer med positiv lutning:
Följande funktion är monoton eftersom den "lutar uppåt" överallt:
För våra exempel gällde det alltså att den inverterbara funktionen var strängt monoton och den icke inverterbara funktionen inte var strängt monoton. Och detta är något som gäller för alla kontinuerliga funktioner (funktioner med sammanhängande grafer som går att rita utan att lyfta pennan). Är en kontinuerlig funktion inverterbar är den också strängt monoton.
Varför gäller då detta? Jo, om en kontinuerlig funktion skall vända nedåt utan att vi får några hopp i grafen måste det ju bildas en slags "bergstopp" () i grafen, och genom den "bergstoppen" kan vi dra en vågrät linje som skär två punkter. Därför kan en kontinuerlig funktion inte vara inverterbar utan att också vara strängt monoton.
Men om vi stryker det där med att funktionen skall vara kontinuerlig behöver vi inte nödvändigtvis få en bergstopp när vi vänder nedåt. Kika exempelvis på följande funktion:
Här kan vi få grafen att tillfälligt peka nedåt utan att bilda en "bergstopp" just för att vi kan göra ett hopp i grafen. Denna funktion är alltså inte kontinuerlig.
Hjälper detta för att ta fram ett motexempel?
Tack så mycket, blev mycket enklare att förstå!
Sinuskurvan borde ju då vara ett motbevis, och då är väl x^2 det med, eftersom de båda är diskontinuerliga funktioner?
Nej, varken eller är diskontinuerliga. De har ju inga "hopp" i sina grafer, eller hur?
De är inte heller motexempel eftersom de inte är inverterbara i något intervall där de är icke-monotona.
AlvinB skrev:Nej, varken eller är diskontinuerliga. De har ju inga "hopp" i sina grafer, eller hur?
De är inte heller motexempel eftersom de inte är inverterbara i något intervall där de är icke-monotona.
Tack för hjälpen, nu har jag förstått. Fick läsa på om diskontinuerliga funktioner :)



