Jag får fel svar trots korrekt metod? Kaströrelse
Uppgift c ger nödvändig information men min fråga handlar om d
Min beräkning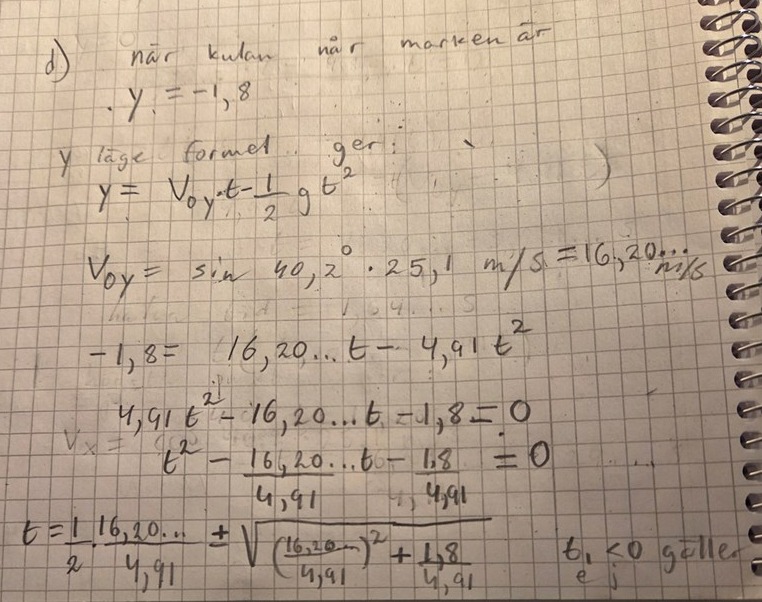
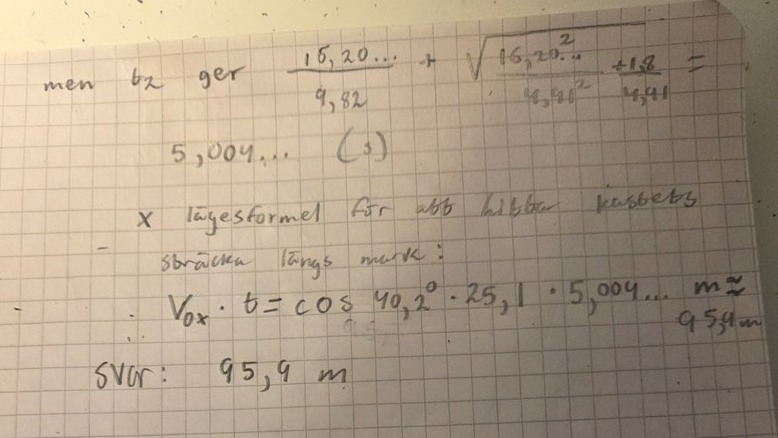
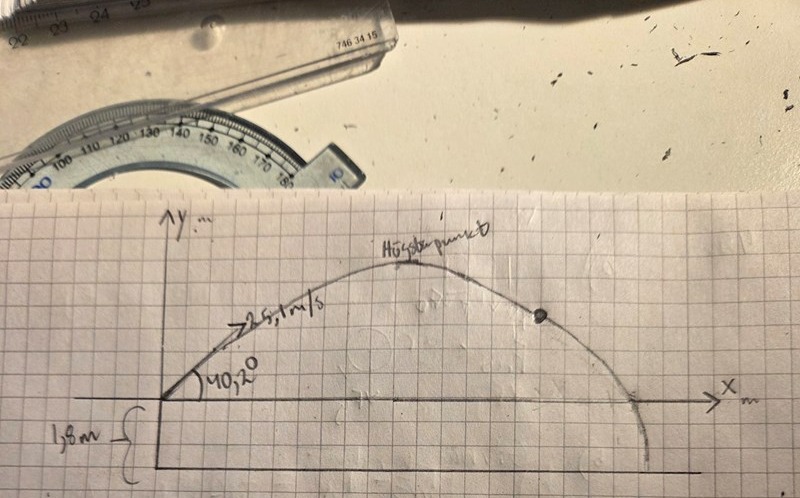
Min fråga och olikheten med facit
Facit säger att svaret ska vara 65,3 meter. Som ni ser får jag 95,9 meter som svar. Så vad är felet i min uträkning? Ska inte y vara -1,8 meter i uträkningen? Jag tror att jag använt den metoden tidigare och det har funkat väl.
Youtube lösning

Jag ser att en youtube video visar denna lösning. Men det är jätte konstigt eftersom y är ju inte 0, den är ju negativ när den når marken?
Liknande uppgift i boken med lösning
Bokens exempel uppgift liknar ju min uppgift och där säger de ju att man ska sätta y till negativ?
Studenten06 skrev:[...]
Min fråga och olikheten med facit
Facit säger att svaret ska vara 65,3 meter. Som ni ser får jag 95,9 meter som svar. Så vad är felet i min uträkning? Ska inte y vara -1,8 meter i uträkningen? Jag tror att jag använt den metoden tidigare och det har funkat väl.
Titta noga på den här delen, här finns ett fel.

Det som är klurigt här är att man måste bestämma själv hur man ser på y-axeln. Här finns inget "ska", utan man väljer själv. Om man bara kopierar boken utan att ha 100% koll så kan det lätt bli fel. Det val man gör påverkar hur man ställer upp ekvationen.
I båda fallen kommer kulan att landa och stanna på en lägre y-nivå än den började. Den släpps i huvudhöjd och landar på marken en bit bort.
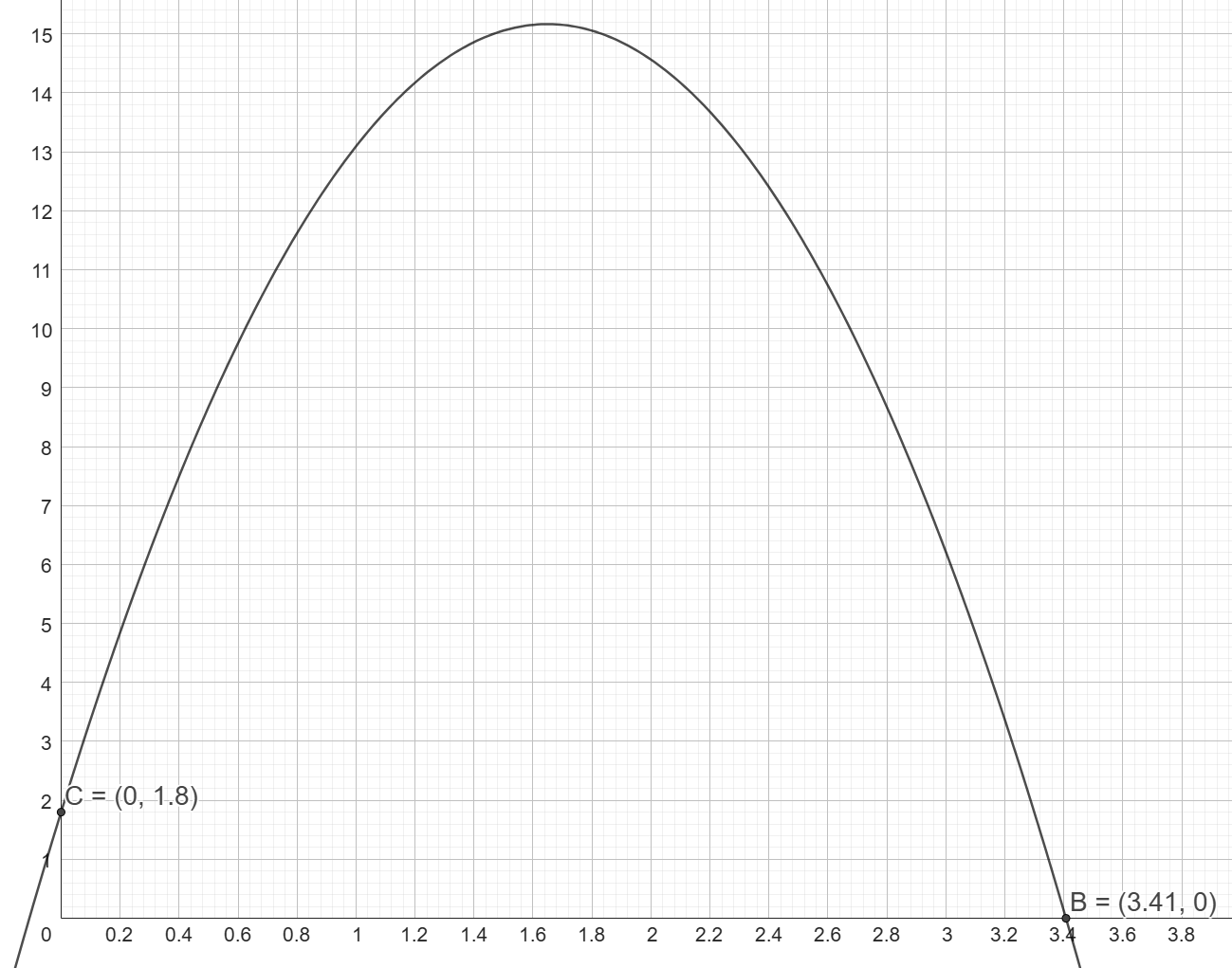
Variant 1 - marknivå är y=0:
Om marknivån är då kulan träffar x-axeln, alltså då y=0, så kommer kulan att börja sin bana ovanför x-axeln. När släggkastaren släpper släggan så är redan y=1,8. Sedan far den i en båge genom luften och landar/stannar då y=0.
Det tar 3,41 sekunder; sträckan blir 65,3 meter. Ungefär.
https://www.geogebra.org/classic/dmybswgr
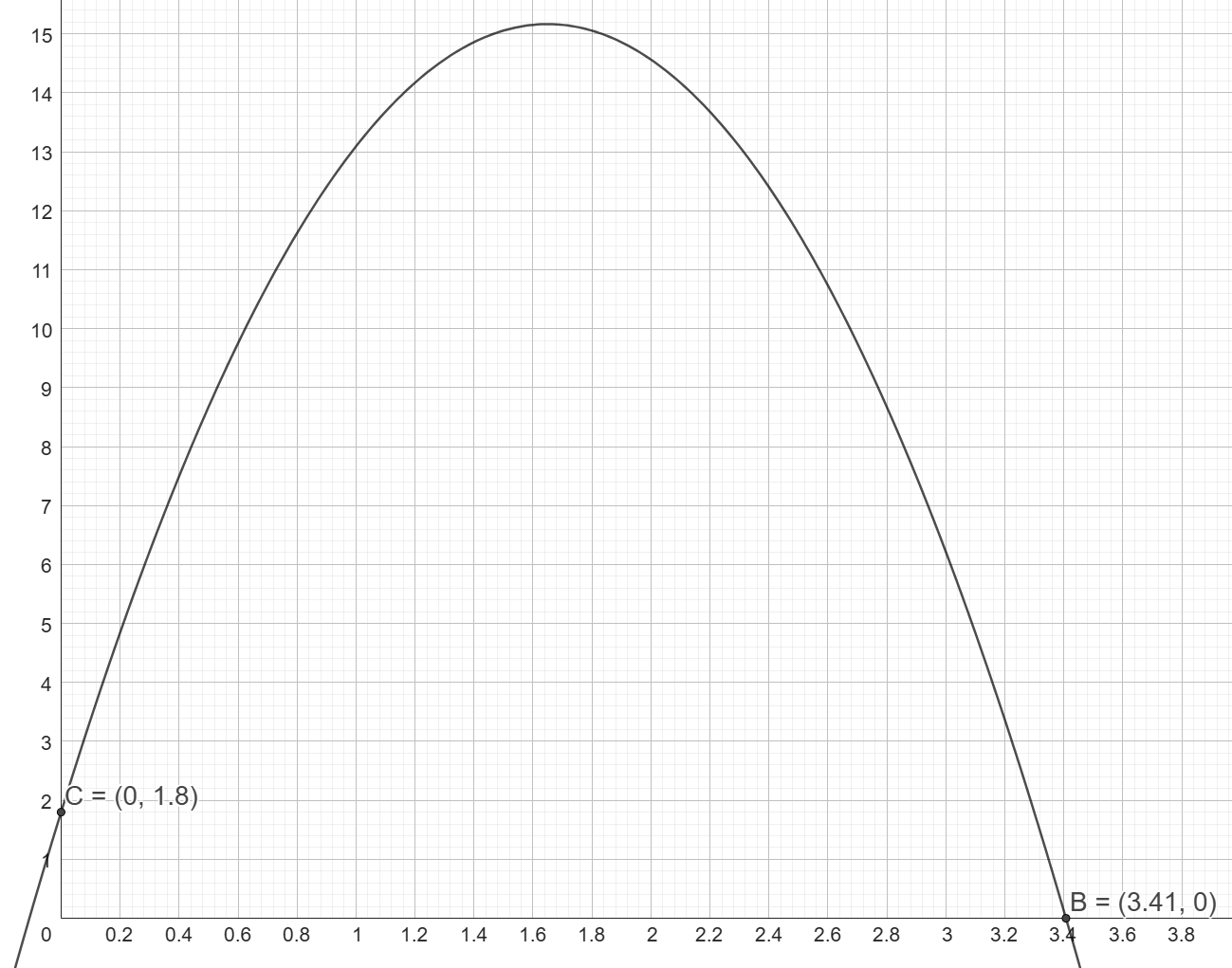
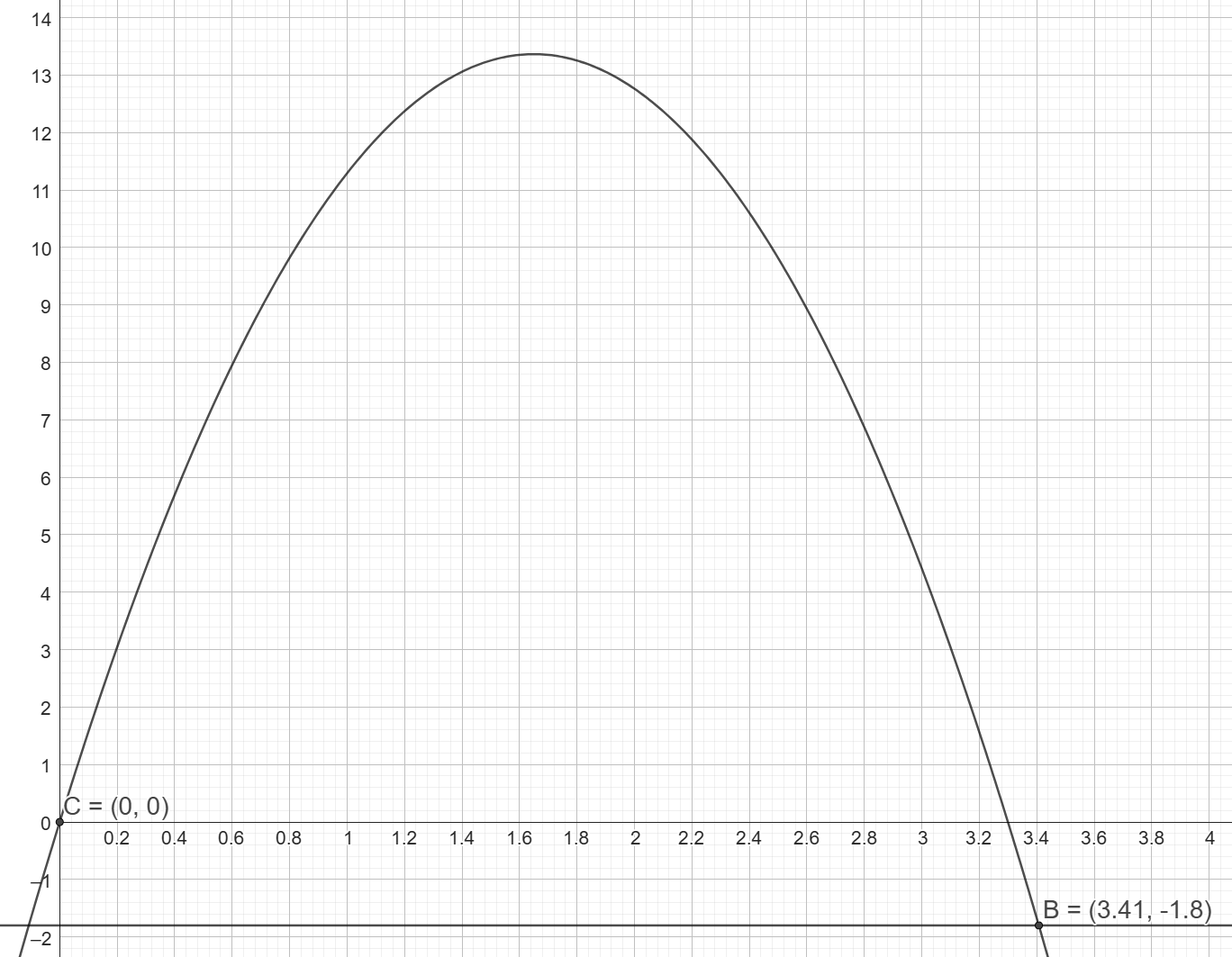
Variant 2 - kulan börjar vid y=0:
Om vi istället sätter att kulan börjar sin färd vid y=0, alltså att det är huvudhöjd, så kommer marknivån att ha ett negativt y-värde.
När släggkastaren släpper släggan så är y=0. Sedan far den i en båge genom luften. När y återigen blir noll så har kulan inte landat på marken. Då är den åter i höjd med huvudet. Sedan minskar y ytterligare och kulan landar på marken då y=-1,8.
Det tar 3,41 sekunder; sträckan blir 65,3 meter. Ungefär.
https://www.geogebra.org/classic/kfw2zncr
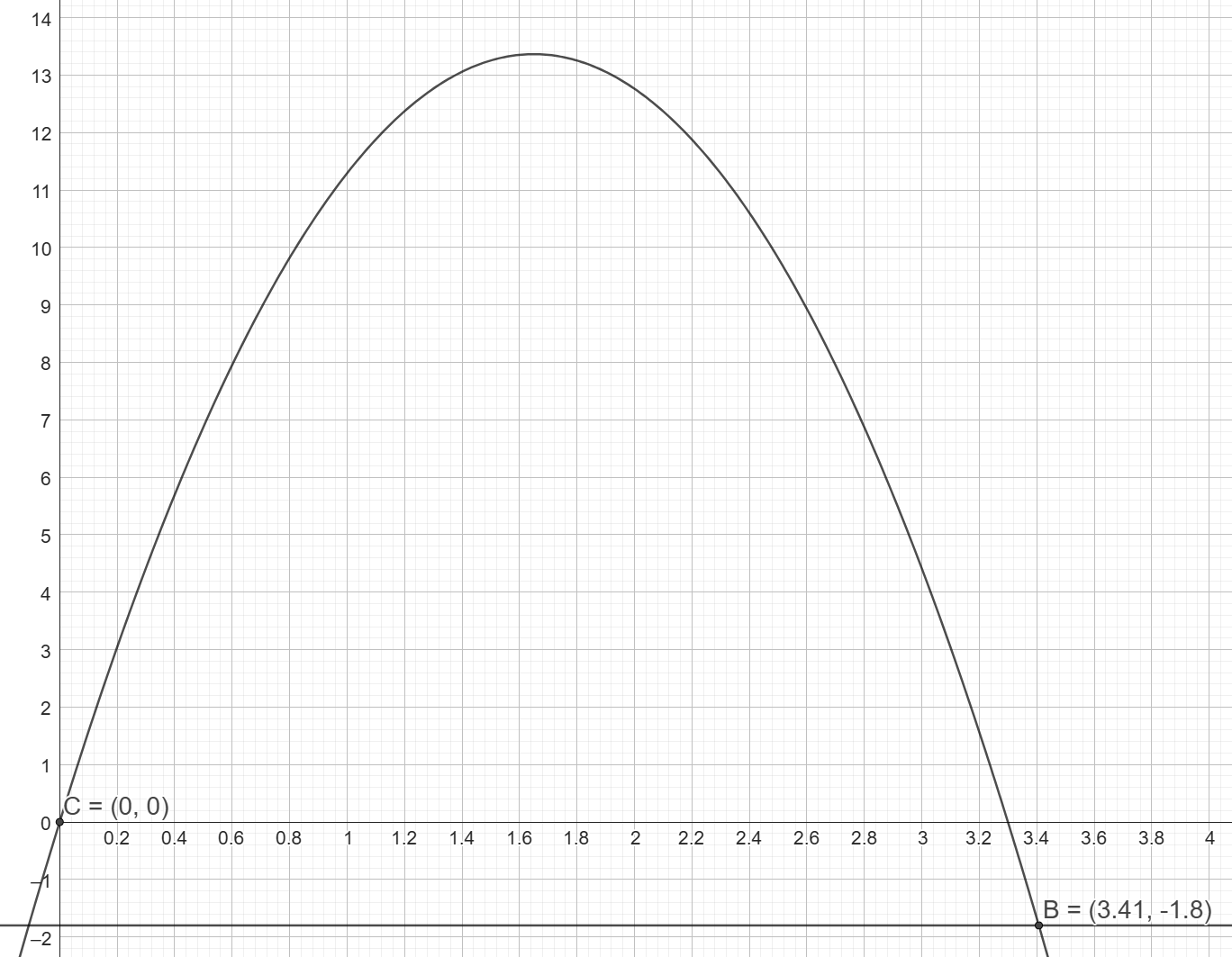
Vad man väljer är upp till en själv. Spontant tycker jag själv det är enklare att tänka att y=0 är marknivå.
sictransit skrev:Det som är klurigt här är att man måste bestämma själv hur man ser på y-axeln. Här finns inget "ska", utan man väljer själv. Om man bara kopierar boken utan att ha 100% koll så kan det lätt bli fel. Det val man gör påverkar hur man ställer upp ekvationen.
I båda fallen kommer kulan att landa och stanna på en lägre y-nivå än den började. Den släpps i huvudhöjd och landar på marken en bit bort.
Variant 1 - marknivå är y=0:
Om marknivån är då kulan träffar x-axeln, alltså då y=0, så kommer kulan att börja sin bana ovanför x-axeln. När släggkastaren släpper släggan så är redan y=1,8. Sedan far den i en båge genom luften och landar/stannar då y=0.
Det tar 3,41 sekunder; sträckan blir 65,3 meter. Ungefär.
https://www.geogebra.org/classic/dmybswgr
Variant 2 - kulan börjar vid y=0:
Om vi istället sätter att kulan börjar sin färd vid y=0, alltså att det är huvudhöjd, så kommer marknivån att ha ett negativt y-värde.
När släggkastaren släpper släggan så är y=0. Sedan far den i en båge genom luften. När y återigen blir noll så har kulan inte landat på marken. Då är den åter i höjd med huvudet. Sedan minskar y ytterligare och kulan landar på marken då y=-1,8.
Det tar 3,41 sekunder; sträckan blir 65,3 meter. Ungefär.
https://www.geogebra.org/classic/kfw2zncr
Vad man väljer är upp till en själv. Spontant tycker jag själv det är enklare att tänka att y=0 är marknivå.
Egentligen tycker jag att origo borde utgå från vart den kastas och det känns mest logiskt. Jag ville inte bara kopiera bokens lösning utan jag tyckte om deras metod. Min uträkning hade ett slarvfel. I alla fall tack så mycket både du och Yngve för ert svar.
Studenten06 skrev:Egentligen tycker jag att origo borde utgå från vart den kastas och det känns mest logiskt. Jag ville inte bara kopiera bokens lösning utan jag tyckte om deras metod. Min uträkning hade ett slarvfel. I alla fall tack så mycket både du och Yngve för ert svar.
Precis! Man väljer det man lättast visualiserar.
Ibland kan problemets formulering göra att det ena är bättre än det andra. Ett problem där något faller till marken kanske gör sig bättre om lägesenergin är positiv först och slutar på noll, istället för noll initialt och sedan negativt.
Ett tredje sätt är att köra med v - t diagram, som ofta ger kortare beräkningar.