Jämvikt

Har du ritat en bild med alla krafter samt komposantuppdelat F_T1 och F_T2? För a) kan du beräkna momentjämvikt runt vänstra änden. I b) kan du se att de horisontella krafterna i repen är lika. 

Så? 

Nej, det där stämmer inte.

Vilket moment är det du tänker på i den rödmarkerade rutan?

Du behöver en kraftekvation också, och ta med kraften från den hängande vikten.

Kämpade liten.  Men tänkte runt sum of torque and force! Hur ser ut?

Jag är inte med på vad dina ekvationer betyder. Kan du förklara i ord?

Jag gissar att du har fel hävarmar någonstans också, men är inte säker.

Jag ser inte att du har delat upp krafterna i repen i vågräta och lodräta komposanter.

free body diagram principen,annars vet jag inte hur? tack

Cristina skrev:

free body diagram principen,annars vet jag inte hur? tack

Om du skulle få ett sådant svar här, tror du att du skulle fatta det?

Som Bubo säger, det krävs text. Också enligt kursplanen: "välutvecklade resonemang".

Jag fattar till exempel inte alls hur du får $F_{\rm S} = 1,\!65 \ {\rm N}$. Värdet verkar vara väldigt litet när det är givet att endast stångens tyngd är redan 120 newton.

Som MrPotatohead skrev: börja med moment kring den vänstra änden. Som om stången var ledad där. Bestäm med vilken kraft den högre linan behöver dra stångens andra ände vertikalt uppåt. Gör en tydlig ritning med skalenliga pilar för krafterna.

Ja, linan drar uppåt med 160 newton.

Hur stor är då spänningen i linan? 

sin (30)* 160= 80 

När du inte svarar på mina frågor kan jag inte hjälpa dig. 

Bubo skrev:

När du inte svarar på mina frågor kan jag inte hjälpa dig. 

Jag gjorde beräkningar med ord! Det är i kronologin! Eller syns inte? Hur behöver jag göra? Tack

Ja, nu ser jag att du har skrivit bättre i inlägg 9. Fel av mig.  Tack.

Men jag har ändå lite svårt att följa ditt resonemang. Det känns kortfattat och ekvationer&figurer hamnar bredvid varandra i stället för att hamna i en logisk följd. Det tar helt enkelt längre tid för mig att läsa. 

Cristina skrev:

sin (30)* 160= 80 

Nej.

Om man inte ser det inför sitt inre öga är det en bra idé att göra en ritning:

nu kommer jag att förstå! tack

Bubo skrev:

Ja, nu ser jag att du har skrivit bättre i inlägg 9. Fel av mig.  Tack.

Men jag har ändå lite svårt att följa ditt resonemang. Det känns kortfattat och ekvationer&figurer hamnar bredvid varandra i stället för att hamna i en logisk följd. Det tar helt enkelt längre tid för mig att läsa. 

precis postat en annat version! mamma mia jag kämpar! tack för stöd

Ja, bra! Nu är det mycket lättare att se hur du tänker.

Momentjämvikt runt den vänstra punkten kommer att ge oss vertikala kraften i den högra punkten, alltså kraften F_T1 gånger cos(30deg). Det är den som blir 160N.

Du har räknat rätt med siffrorna, men så har du skrivit att 160N är kraften F_T2 gånger sin(theta).

Det är ju fel kraft (och därmed fel vinkel) och sinus i stället för cosinus. Kraft som angriper i en punkt kan inte ge moment runt den punkten.

Två misstag, som är lätta att hitta därför att du skrev tydligare. Rätta dem, så får du säkert rätt svar.

Så här blir 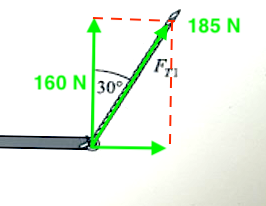$F_{\rm T1}= \dfrac{160 \ {\rm N}}{\cos 30^\circ}$:
Sidorna i en sådan rätvinklig triangel förhåller sig som $1:2:\sqrt{3}$ där tvåan är hypotenusan. Igen: om man inte ser det inför sitt inre öga är det alltid bra att göra en noggrann ritning.

Ja,  rätt. Bra.

Du tog moment om högre änden. Jag tror det kan lite enklare, att bestämma den vertikala komposanten i F_T2 från kraftsumman i vertikal led: 400 + 120 - 160 = 360 newton. Och horisontell komposant är $360 \tan 30^\circ= 92,\!3 \ {\rm N}$.

Så den sökta vinkeln blir $\theta = \arctan \dfrac{92,\!3}{360} = 14,\!4^\circ$.