Jämviktsproblem med hängande balk

Hej! Jag sitter fast på denna uppgift. Rätt svar är enligt facit alternativet $-mgL\cos \beta + 2SL(\cos\alpha \cos \beta + sin \alpha sin \beta)$ . Jag hade glömt bort den trigonometriska identiteten $cos(\alpha - \beta) = \cos\alpha \cos \beta + sin \alpha sin \beta$ , men den biten lossnade till sist. Däremot känner jag mig fortfarande lite osäker på hur jag ska gå till väga för att komma till det svaret. (Det här är nog egentligen en ren matefråga om trigonometriska identiteter, förutsatt att jag ställt upp ekvationen rätt)

Jag ställde upp momentekvationen enligt

$\circlearrowleft: -mgL\cos\beta - mgL\sin \beta + 2SL\sin\alpha + 2SL\cos\alpha=0$

Men hur man kommer därifrån till

$-mgL\cos \beta + 2SL(\cos\alpha \cos \beta + sin \alpha sin \beta)$ är min fråga.

Som alltid, otroligt tacksam för all input!

Det gör du inte, för din ekvation ser inte rätt ut. Tex uttrycker de två sista termerna inte ens moment - de har storheten kraft och inte moment.

Tillägg: 25 feb 2024 13:15

Kanske lite hjälp.

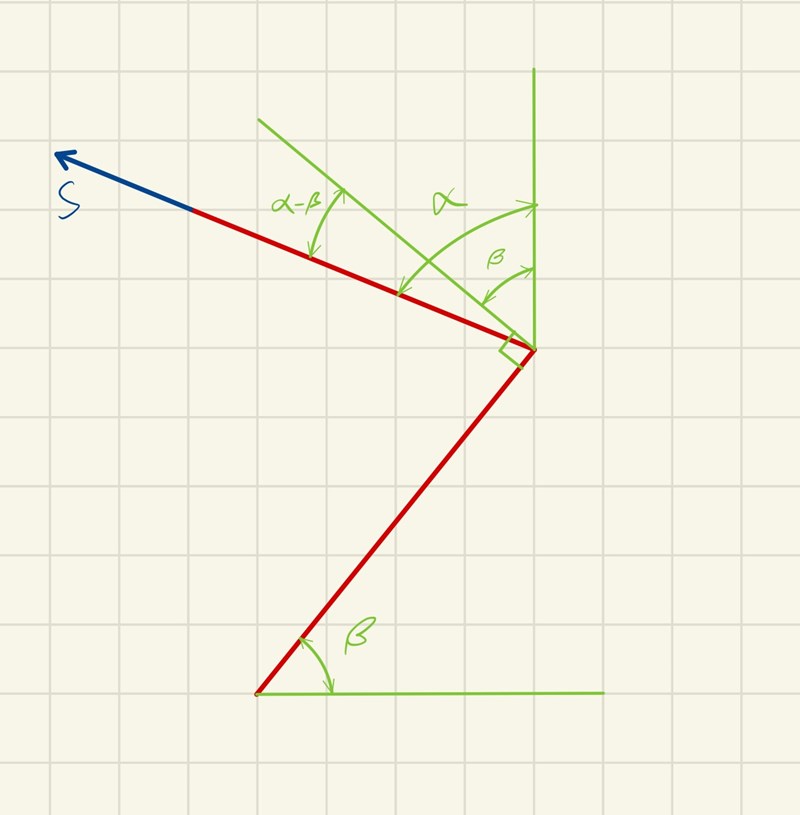
PATENTERAMERA skrev:
Det gör du inte, för din ekvation ser inte rätt ut. Tex uttrycker de två sista termerna inte ens moment - de har storheten kraft och inte moment.

Tillägg: 25 feb 2024 13:15

Kanske lite hjälp.

Sorry! Jag skrev av fel från mina uträkningar på papper. Det ska självklart stå ett $L$ i de sista termerna. Stämmer ekvationen nu?

Men jag antar ändå att man direkt bör göra som du gjort i din figur. Jag missade hur relationen $\alpha-\beta$ såg ut, tack för figuren!

Alright, nu har jag fått fram ur figuren att $S_y = Scos(\alpha -\beta)$ . Jag fick fram från tidigare att den vertikala komposanten av tyngdkraften är $-mgcos(\beta)$ . Sätter man in hävarmarna $2L$ respektive $L$ samt använder att både $S_x$ och horisontella komposanten av tyngdkrafen har sin verkningslinje som går genom $A$ så jag fram rätt uttryck.

Låter det rätt tänkt? (Jag tänker mig att koordinatsystemet är orienterat så att x-axeln är orienterad med samma lutning som balken)

Du menar y-komponenten av tyngdkraften? Annars är den vertikala komponenten av tyngdkraften mg, eftersom tyngdkraften verkar vertikalt, dvs nedåt.

Ja, annars låter det rätt.

PATENTERAMERA skrev:
Du menar y-komponenten av tyngdkraften? Annars är den vertikala komponenten av tyngdkraften mg, eftersom tyngdkraften verkar vertikalt, dvs nedåt.

Ja, annars låter det rätt.

Jag menar y-komponenten, sorry:)

Bra, då hänger jag med. Tusen tack för din hjälp!

Svara

Visa senaste svar