Järnrör

A och B verkar riktiga, men jag förstår inte vad det är du har gjort på C. Du verkar ha räknat ut hur mycket tomrummet inuti röret skulle ha vägt, om det hade varit gjort av järn. Det är inte det man frågar efter.

Standardfråga 1a: Har du ritat?

Ska jag beräkna mantelytans vikt? 

Dvs 7,9*1413

Renny19900 skrev:

Ska jag beräkna mantelytans vikt? 

Dvs 7,9*1413

Nej mantelytan är ingen volym, så den har ingen vikt.

Du ska först räkna ut hur mycket järn (dvs hur många cm^3 järn) röret består av.

Enklast är nog då att du tänker dig att du klipper upp röret på längden och viker ut det till en rektangel (egentligen ett rätblock eftersom vi ska räkna med tjockleken).

Hur stor volym upptar detta rätblock av järn?

När du vet volymen så kan du beräkna vikten med hjälp av densiteten (massa = volym*densitet).

Yngve skrev:

Renny19900 skrev:

Ska jag beräkna mantelytans vikt? 

Dvs 7,9*1413

Nej mantelytan är ingen volym, så den har ingen vikt.

Du ska först räkna ut hur mycket järn (dvs hur många cm^3 järn) röret består av.

Enklast är nog då att du tänker dig att du klipper upp röret på längden och viker ut det till en rektangel (egentligen ett rätblock eftersom vi ska räkna med tjockleken).

Hur stor volym upptar detta rätblock av järn?

När du vet volymen så kan du beräkna vikten med hjälp av densiteten (massa = volym*densitet).

Man kan vika ut röret till en rektangel, men när det är så pass tjockt så blir det ett lite annat svar än om man tar totalytan minus innerytan (den tomma delen). Det kan vara intressant att göra båda.

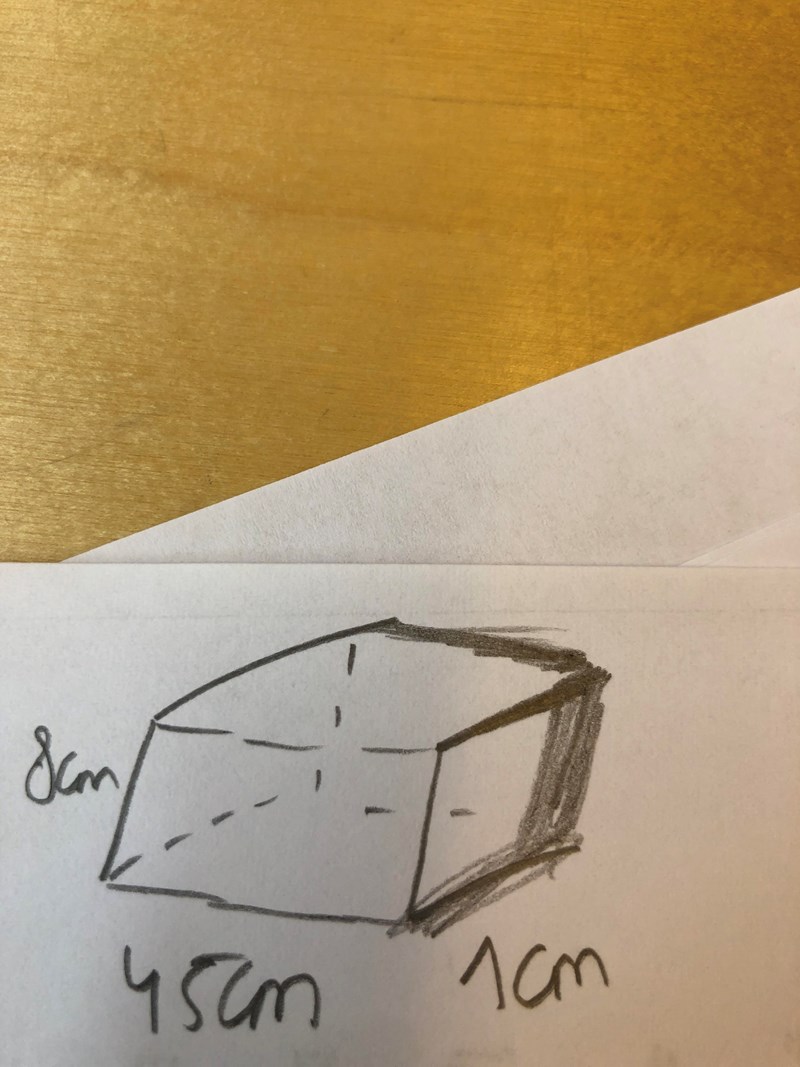Jag fattar inte hur jag ska rita den. Järnröret är en cylinder. Om jag beräknar mantelarean*höjden -> begränsingsarean av cylinder -> som då blir en rektangeln 

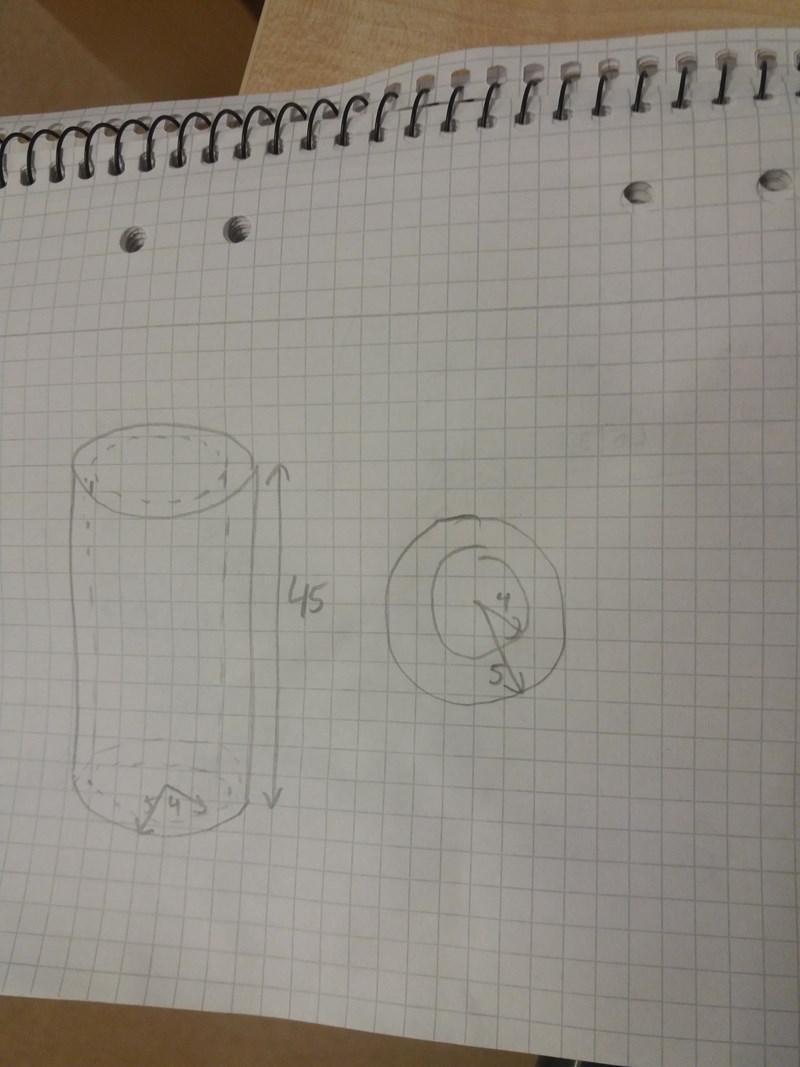
För att beräkna järnrörets volym beräknar man arean av cirkelringen och multiplicerar den med rörets längd. För att få fram rörets massa multiplicerar man rörets volym med densiteten.

Ta en toarulle, klipp upp den längs med. Det du får då är en rektangel. Tjockleken på pappen i rullen motsvarar tjockleken av ditt rör. Rita det genom att rita ett rätblock som du gjort. En sida är tjockleken (1 cm) en sida är längden (45 cm) och den sista sidan är omkretsen (2*pi*r).
Med denna metod är det viktigt vilken diameter du väljer. Innerdiametern ger inte samma svar som ytterdiametern. Rätt svar fås genom att välja genomsnittsdiametern.

#####################

Alternativ lösning:
Räkna först ut volymen på ett cylinder med diametern 8+1+1=10 cm och längden l=45 cm

$V_y=\mathrm{\pi }·(r_y{)}^2·l$ 

Ta sedan bort 'hålet' som är en cylinder med diametern 8cm och längden 45cm

$V_i=\mathrm{\pi }·({\mathrm{r}}_{\mathrm{i}}{)}^2·\mathrm{l}$

rörets volym blir då $V_y-V_i$

Testa att räkna med bokstäver så långt du kan och förenkla ditt uttryck.

Smaragdalena skrev:

För att beräkna järnrörets volym beräknar man arean av cirkelringen och multiplicerar den med rörets längd. För att få fram rörets massa multiplicerar man rörets volym med densiteten.

Cirkel area = r^2*pi 

i detta fall måste vi ta Storacirklens area - lilla cirkelns area * höjden (45cm). 

Det blir  (5^2*pi-4^2*pi)*45=1272cm^3

1272*7,9= 10 049 g (avrundar)

joculator skrev:

Ta en toarulle, klipp upp den längs med. Det du får då är en rektangel. Tjockleken på pappen i rullen motsvarar tjockleken av ditt rör. Rita det genom att rita ett rätblock som du gjort. En sida är tjockleken (1 cm) en sida är längden (45 cm) och den sista sidan är omkretsen (2*pi*r).
Med denna metod är det viktigt vilken diameter du väljer. Innerdiametern ger inte samma svar som ytterdiametern. Rätt svar fås genom att välja genomsnittsdiametern.

#####################

Alternativ lösning:
Räkna först ut volymen på ett cylinder med diametern 8+1=9 cm och längden l=45 cm (min fetning)

$V_y=\mathrm{\pi }·(r_y{)}^2·l$ 

Ta sedan bort 'hålet' som är en cylinder med diametern 8cm och längden 45cm

$V_i=\mathrm{\pi }·({\mathrm{r}}_{\mathrm{i}}{)}^2·\mathrm{l}$

rörets volym blir då $V_y-V_i$

Testa att räkna med bokstäver så långt du kan och förenkla ditt uttryck.

Då får du fel svar. Godstjockleken skall vara 1 cm, och då blir ytterdiametern 10 cm, inte 9 cm.

Tack!
Renny19900 såg det själv   :-)

Är min uträkning isåfall rätt? (5^2*pi-4^2*pi)*45=1272cm^3 

1272*7,9= 10 049 g

Ja.

$(5^2-4^2)·\mathrm{\pi }·45=9·\mathrm{\pi }·45\approx 1272$

Edit:  Men du skall inte avrunda på vägen. Du har ju inte kommit hela vägen. Räkna med exakta siffror hela vägen.
Rätt vore att räkna:

405*pi*7,9=10051,52  och sedan avrunda till 10052

Ok. Tack för hjälpen :-)

Det var ju en mycket bättre metod än den jag först föreslog (att klippa upp järnröret på längden), efrersom mitt förslag endast skulle ge ett närmevärde till järnvolymen.

Som Laguna skrev så kan det vara intressant att se hur stor skillnad det blir med de olika uträkningarna.

Om vi klipper upp järnröret och viker ut det så blir det nästan ett rätblock.

Kroppen har längd $45$ cm, tjocklek $1$ cm och bredd $8\pi$ eller $10\pi$ cm, beroende på om vi använder inre eller yttre omkrets som bredd.

Om vi använder $8\pi$ cm som bredd får vi volymen $45\cdot 1\cdot 8\pi\approx 1131$ $cm^3$

Om vi använder $10\pi$ cm som bredd får vi volymen $45\cdot 1\cdot 10\pi\approx 1414$ $cm^3$

Medelvärdet av bredden, dvs $9\pi$ cm, ger precis som joculator skrev rätt värde på volymen, nämligen $45\cdot 1\cdot 9\pi\approx 1272$ $cm^3$