Jordbävning.

Det du vill göra är att helt sonika välja ut två magnituder på skalan, säg "M1" där M=1, och "M2" där M=2, och sedan jämföra dem med varandra för att se hur stor skillnaden i energinivåer är.

M1 = (2/3) * ( lg(E1) - U)

M2 = (2/3) * ( lg(E2) - U)

Nu vill du räkna ut M2 - M1 (M2-M1 = ... - ...), och sedan få en E2/E1-term på ena sida för att därmed kunna visa hur många gånger större E2 är än E1. Du borde få ett svar som är 31.6227...

Kom ihåg att M2-M1 = 1, eftersom det bara är ett steg på skalan.

Jag förstår inte. 

Du vill jämföra den energi $E_1$ som frigörs vid en jordbävning där magnituden är M+1, med den energi $E_2$ som frigörs vid en jordbävning där magnituden är M. Du vill alltså ta reda på vilket värde kvoten $\frac{E_1}{E_2}$ har.

Du har korrekt kommit fram till att $lg(E)=\frac{3M}{2}+K$

Detta innebär att $E=10^{\frac{3M}{2}+K}=10^{\frac{3M}{2}}\cdot 10^K$

Det gäller alltså att

$E_1=10^{\frac{3(M+1)}{2}}\cdot 10^K$

$E_2=10^{\frac{3M}{2}}\cdot 10^K$

Ställ nu upp ett uttryck för $\frac{E_1}{E_2}$ och beräkna dess värde.

Varifrån har du fått andra uttrycket, där du har plus1, Yngve? 

Hur kan räkna det här nu? Kan jag förkorta bort något av det här

Päivi skrev :

Varifrån har du fått andra uttrycket, där du har plus1, Yngve? 

I uppgiften står det:

Om en jordbävning har magnituden M (dvs M på Richterskalan) så har en jordbävning med ett stegs ökning på Richterskalan magnituden M+1.

Päivi skrev :

Hur kan räkna det här nu? Kan jag förkorta bort något av det här

Du bytte nu uttryck mellan $E_1$ och $E_2$ jämfört med vad jag skrev.

Jag byter tillbaka:

Om $E_1={10}^{\frac{3(M+1)}{2}}·{10}^K$ och $E_2={10}^{\frac{3M}{2}}·{10}^K$ så är $\frac{E_1}{E_2}=\frac{{10}^{\frac{3(M+1)}{2}}·{10}^K}{{10}^{\frac{3M}{2}}·{10}^K}$

Detta uttryck går att förenkla rejält. Ta ett steg i taget.

Det ska jag göra. 

Snyggt, där har du det. Jag var lat i min lösning där jag helt enkelt stoppade in två värden på M:en, men det du gjort där enligt Yngves tips blir snyggare måste jag säga :)

Bra Päivi.

Jag skulle helst se att du som ett mellansteg först faktoriserade $10^{\frac{3(M+1)}{2}}$ till $10^{\frac{3M}{2}}\cdot 10^{\frac{3}{2}}$ innan du förkortade med nämnaren.

Bättre. Nu är jag nästan nöjd. Nu saknar jag bara att du byter ut det felaktiga plustecknet (rödmarkerat) mot ett multiplikationstecken i höjd med täljarens faktorer.

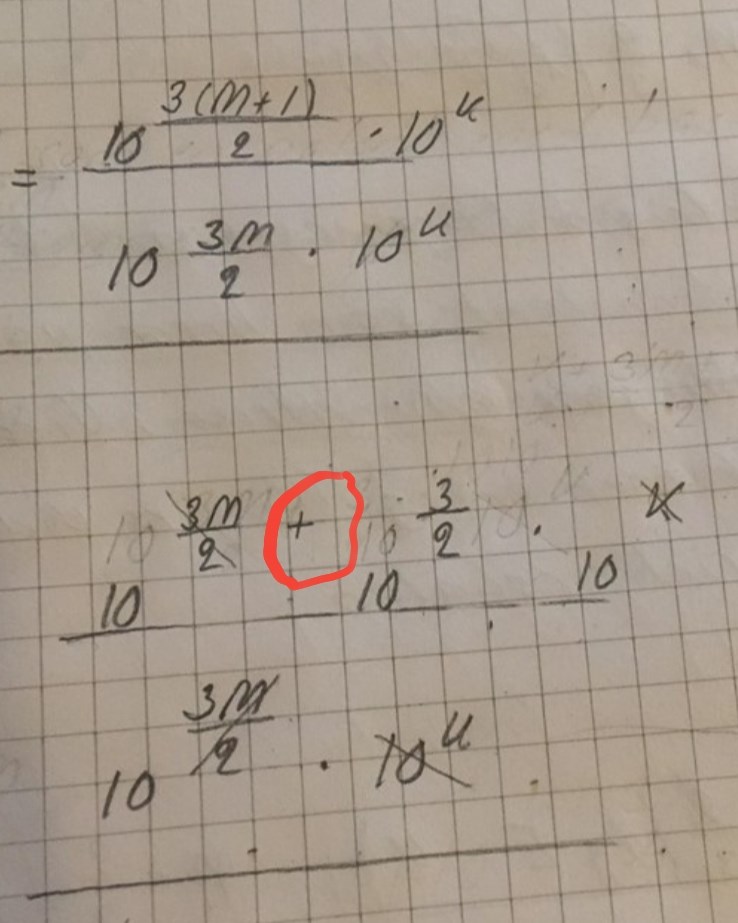
Det ska jag göra, Yngve!

Tusen tack Yngve för det här!!!