K^2*(C(n,k))
Hejsan!
Jag vill skriva om detta uttryck k^2*(C(n,k)) så att faktorn k försvinner och ersätts med n istället. På samma sätt som k*(C(n,k))=n*(C(n-1,k-1))
När jag gör samma sak med k^2*(C(n,k)) lyckas jag bara skriva om det till följande uttryck
k^2*(C(n,k))=kn*(C(n-1,k-1))
Hur går jag till vägar?
Menar du att det alltid går? Det är inte säkert att k alltid förekommer som faktor två gånger.
Är inte helt säker. Grejen är att jag ska beräkna en summa där k=0 går från noll n. I denna summa förekommer uttrycket k^2*(C(n,k)). Summa-uttrycket vill jag göra om till en binomialsats, men då måste k bort eftersom det inte är en konstant.
Kan du visa hela summauttrycket?
Det kan jag göra, ber om ursäkt om det ser rörigt ut, skriver från mobilen. Så vet inte hur man skriver summatecknet
(Summa där k=0 går till n)k^2*(C(n,k))*t^k*(1-t)^(n-k)
Är uttrycket ? Vad är ?
Det stämmer jättebra. Oj förlåt, glömde nämna det.
0<t<1
Kan du skriva av ursprungsuppgiften ord för ord eller lägga in en bild av den? Det är lättare att hjälpa till då.
Beräkna följande summa där n är ett positivt heltal och 0<t<1
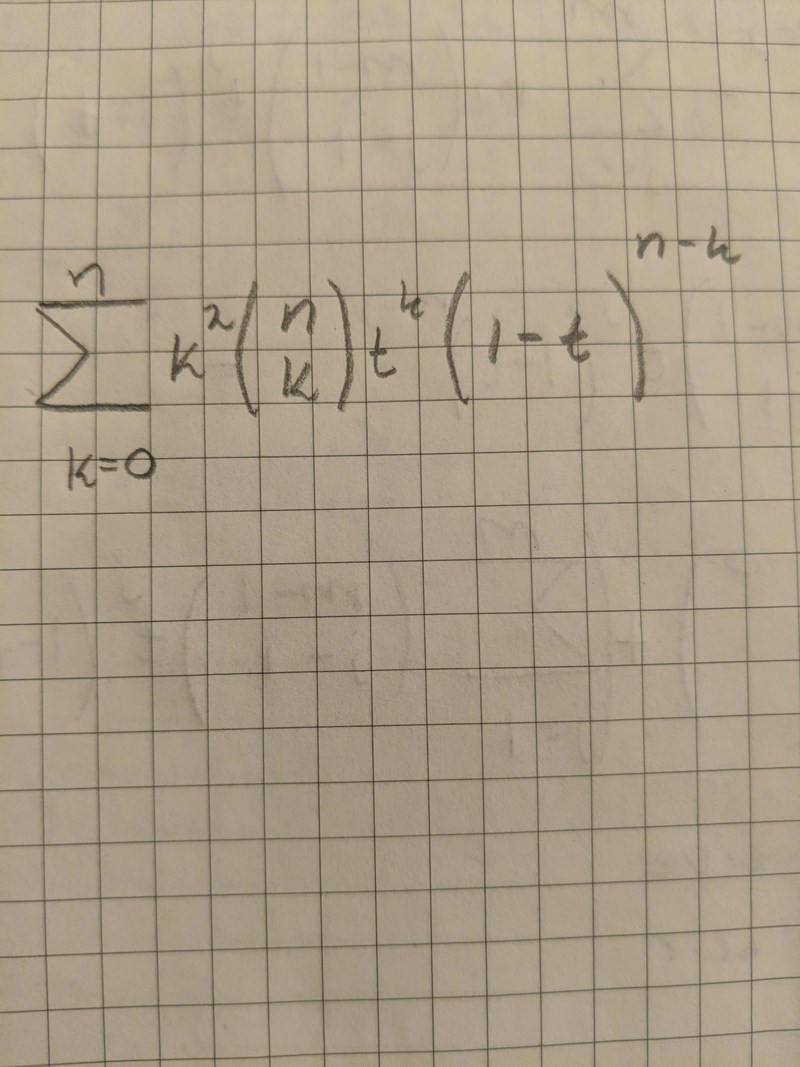
Finns det något sätt man byta ut k:et, eller måste jag hitta en annan väg att gå?
Jag skulle börja med att beräkna uttryckets värde för n = 1, 2, 3, 4, kanske 5 och se om jag hittar något mönster.
Okej då tänkte jag såhär.
Vi måste göra om den nedre gränsen, om k=0 blir hela uttrycket 0. Därför använder jag gränsen k=1 till n och räknar att k alltid är lika med 1 när vi ökar n:s värde
Om n= 1,2,3,4,5 kommer summan bli som följande :
t
2t-(2t^2)
3t-(6t^2)+(3t^3)
4t-(12t^2)+(12t^3)-(4t^4)
5t-(20t^2)+(30t^3)-(20t^4)+(5t^5)
Sambandet jag ser mellan dessa summor kan beskrivas med följande formel
nt(1-t)^(n-k)
Vad gör jag med denna vetskap?
Vad gör jag med denna vetskap?
En gränsvärdesberäkning. Vad blir det, när n går mot oändligheten?
Gränsvärdesberäkningar har jag tyvärr inte övat på sedan matte 3, så den delen sitter tyvärr inte så bra. Men det ser inte ut som att ekvationen har ett tydligt gränsvärde?
Tar tillbaka det jag sa, det verkar som att när n går mot oändligheten så blir talet 0?
Vad gör jag med detta?
Är det något jag missar?
henkzzzzzz, det står i Pluggakutens regler att du måste vänta åtminstone 24 timmar innan du bumpar din tråd. 2 timmar är inte tillräckligt. /moderator



