Kalkylark

Säg att du sätter in $x$ kr per år. Om du vill ha 8000 kr på kontot efter första insättningen så måste självfallet $x=8000$. Om du vill ha 8000 kr på kontot efter andra insättningen, så kommer du ha $1,04x$ från den första insättningen och $x$ från den andra, vilket betyder att

$8000 = 1,04x + x$.

Om du vill ha 8000 kr efter tre insättningar, så kommer du efter andra insättningen ha

$1,04x + x$, och

$1,04(1,04x + x) + x = 1,04^2 x + 1,04x + x$

efter tredje insättningen. Det som står i parentesen ovan är beloppet på kontot efter andra insättningen, som alltså växer med ytterligare 4%. Sedan lägger vi till ett till $x$ för vår tredje insättning. Vi får ekvationen $8000 = 1,04^2 x + 1,04x+x$.

Fortsätter vi på liknande vis inser vi snart att vi har med en geometrisk serie att göra. Vi kan då använda formeln för summan av de första $n$ termerna i en geometrisk serie för att ställa upp en ekvation.

Men detta går väl ändå inte att applicera i ett kalkylark? Tanken är att jag ska försöka lösa uppgiften med hjälp av kalkylark.

Man kan låta kalkylarket göra upprepade beräkningar.

Behållningen_ett_år = Behållningen_förra_året * 1.04 + Insättning

Testa för lite olika värden på Insättning.

Lite som när man gör det som vanligt, att man har en viss summa och låter den växa till i detta fallet 8000 kr och ser hur lång tid det tar. Fast att man istället gör det åt andra hållet? att det minskar från 8000 kr? Kan man göra på det viset? Skulle räntesatsen fortfarande vara samma då?

Så här kan det se ut med ett kalkylark:

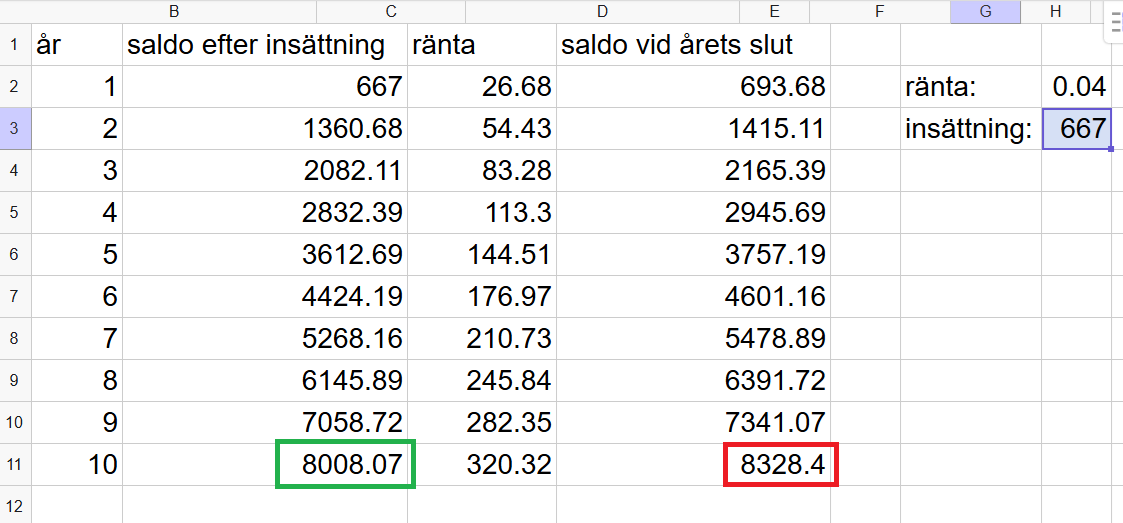
Uppgiften är dock lite lurig. De frågar efter hur mycket han skall spara per år för att saldot på kontot skall vara 8000 kr efter tionde insättningen. Eftersom de talar om årsränta räknar jag med att han sätter in pengar 1 januari och räntan beräknas (och sätts in på kontot) 31 december.

Det betyder att saldot skall vara 8000 kr efter tionde insättningen, men inte efter tionde ränteutbetalningen.

Se min gröna respektive röda ruta. Om man räknar med 8000 kr vid årets slut efter tionde insättningen kan han spara lite mindre per år.

Arket finns här om du vill labba lite själv: https://www.geogebra.org/classic/gmud6daf 

Jag tror jag förstår nu. Jag var nära på att fråga hur du kom fram till att insättningen skulle vara 667 per år men sedan slog det mig att man kan skapa en helt vanlig kalkyl, som om man redan visste vad insättningen var. Om man tex skulle säga att insättningen var 600 kr så hade man kunnat skapa hela denna kalkyl utifrån det, och sedan ändra värdet på insättningen tills värdet på det tionde året uppnådde 8000.

KlmJan skrev:

Jag tror jag förstår nu. Jag var nära på att fråga hur du kom fram till att insättningen skulle vara 667 per år men sedan slog det mig att man kan skapa en helt vanlig kalkyl, som om man redan visste vad insättningen var. Om man tex skulle säga att insättningen var 600 kr så hade man kunnat skapa hela denna kalkyl utifrån det, och sedan ändra värdet på insättningen tills värdet på det tionde året uppnådde 8000.

Det var så jag gjorde. Jag började med 500 spänn om året. Såg att det blev för lite pengar. Därefter ökade jag ...

tack så mycket för hjälpen