3
svar
181
visningar
Rasmusk är nöjd med hjälpen
Kan man bestämma A och B så att funktionen f(x) blir kontinuerlig?
Tjena! Behöver hjälp att förstå hur man ska lägga upp räkningen här. Var börjar jag? Var fortsätter jag? Är helt lost. Läraren är dålig på att förklara.
Vet att men sen tar det stopp.
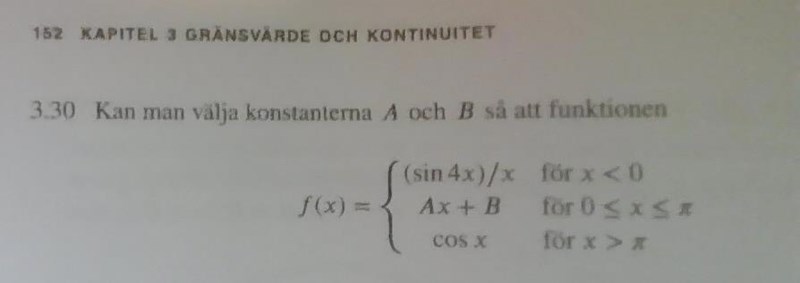
Bestäm och så att:
samt
tomast80 skrev:Bestäm och så att:
samt
För både (sin4x)/x och Cos x då eller?
Du har 2 ställen där funktionen byter mellan uttryck. För att få den kontinuerlig behöver du se till att den gamla och nya formeln ger samma värde i de 2 punkterna, att de möts på mitten.
Räkna ut gränsvärdet för första och andra funktionen i 0 och skriv att de ska vara lika, och likadant för andra och tredje funktionen i pi. Sen har du två ekvationer som du kan lösa ut dina okända tal ifrån.



