Kaströrelse uppgift 119
Är ekvationssystem som gäller? Eller ska man likställa dessa? Jag vill eliminera tiden och beräkna vinkeln.


När du har samma rubrik som din andra tråd är det lätt att tro att det är en dubbelpost
Smaragdalena skrev:När du har samma rubrik som din andra tråd är det lätt att tro att det är en dubbelpost
Ursäkta, ändrat nu.
Det ser ut os om du inte har räknat med att bollen slås iväg från en punkt 0,5 m ovanför marken.
Smaragdalena skrev:Det ser ut os om du inte har räknat med att bollen slås iväg från en punkt 0,5 m ovanför marken.
Just ja, jag lägger in ett koordinatsystem vid marken. Då adderar jag 0,50m i första ekvationen, hur gör man sen?
Om tennisnätet ligger på symmetrilinjen så vet du även att y(20) = 0,5.
Alternativt kan du använda dig av att y'(10) = 0.
Smaragdalena skrev:Om tennisnätet ligger på symmetrilinjen så vet du även att y(20) = 0,5.
Alternativt kan du använda dig av att y'(10) = 0.
Gäller detta fråga b? Hänger inte med
Nej, det är fråga a. Om maximipunkten är precis ovanför nätet, så...
Smaragdalena skrev:Nej, det är fråga a. Om maximipunkten är precis ovanför nätet, så...
Ja där är V=0, men jag har fortfarande 2 okända. Tänkte du så när du skrev y’(10)?
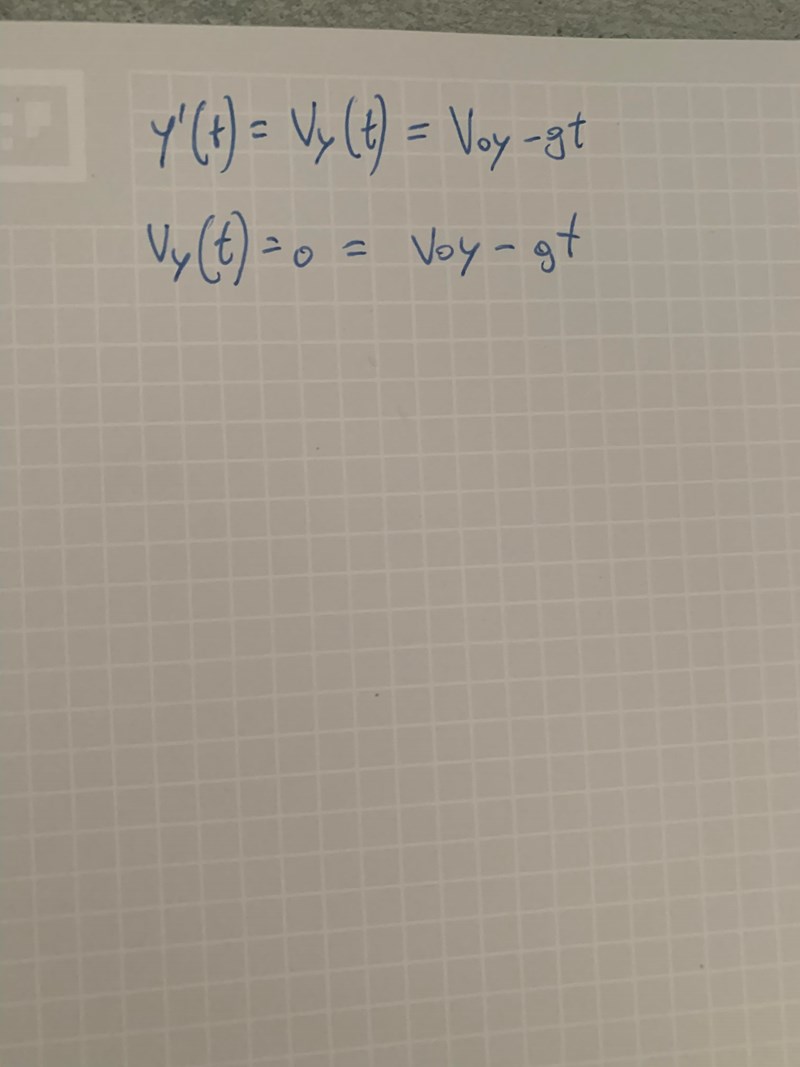
Nej, hastigheten V är inte 0 i maxpunkten, däremot är hastigheten i y-led 0 där.
Kan du hitta ett uttryck som ger hur lång tid det tar för bollen att hinna fram till nätet som en funktion av vinkeln?
Smaragdalena skrev:Nej, hastigheten V är inte 0 i maxpunkten, däremot är hastigheten i y-led 0 där.
Kan du hitta ett uttryck som ger hur lång tid det tar för bollen att hinna fram till nätet som en funktion av vinkeln?
Nej jag vet inte hur det uttrycket skulle se ut... men jag har en fundering, kan man inte använda energiprincipen för att för att ta fram höjden? Men hur som helst, jag hade kommit så långt (se bild)

Multiplicera med cos(a) på båda sidor, använd formeln för dubbla vinkeln, räkna ut vinkeln.
Smaragdalena skrev:Multiplicera med cos(a) på båda sidor, använd formeln för dubbla vinkeln, räkna ut vinkeln.
Precis! Men jag vet inte vad jag ska med 0,50 till.
Hur får du fram 0,5?
Smaragdalena skrev:Hur får du fram 0,5?
0,5 är avståndet där bollen befinner sig när t=0
Det värdet påverkar inte stor vinkeln blir. Det värdet behövs för b-uppgiften.
Smaragdalena skrev:Det värdet påverkar inte stor vinkeln blir. Det värdet behövs för b-uppgiften.
Okej, men dåså, då löser jag a),Ska fortsätta imorgon.
kan du visa hur du menade ”
Om tennisnätet ligger på symmetrilinjen så vet du även att y(20) = 0,5.
Alternativt kan du använda dig av att y'(10) = 0.”
OCH
”Kan du hitta ett uttryck som ger hur lång tid det tar för bollen att hinna fram till nätet som en funktion av vinkeln?”
kan du visa hur du menade ”
Om tennisnätet ligger på symmetrilinjen så vet du även att y(20) = 0,5.
Alternativt kan du använda dig av att y'(10) = 0.”
OCH
”Kan du hitta ett uttryck som ger hur lång tid det tar för bollen att hinna fram till nätet som en funktion av vinkeln?”
När jag räknade lite till visade det sig att man klarade sig utan båda dessa tankesätt. Vill du veta ändå?
Smaragdalena skrev:kan du visa hur du menade ”
Om tennisnätet ligger på symmetrilinjen så vet du även att y(20) = 0,5.
Alternativt kan du använda dig av att y'(10) = 0.”
OCH
”Kan du hitta ett uttryck som ger hur lång tid det tar för bollen att hinna fram till nätet som en funktion av vinkeln?”
När jag räknade lite till visade det sig att man klarade sig utan båda dessa tankesätt. Vill du veta ändå?
Ja gärna, och även om hur man kunde ställa upp ett uttryck om hur lång tid det tog som en funktion av vinkel
Du har ju nästan kommit fram till ett uttryck för tiden det tar att komma fram till nätet som en funktion av vinkeln:
10 = 25 cos(a) . t, lös bara ut t.
Sedan har du ju även kommit fram till ett användbart uttryck längst ner på pappret (idag 13:52). Läste du tipse om hur du skall gå vidare, som jag skrev strax under?
Smaragdalena skrev:Du har ju nästan kommit fram till ett uttryck för tiden det tar att komma fram till nätet som en funktion av vinkeln:
10 = 25 cos(a) . t, lös bara ut t.
Sedan har du ju även kommit fram till ett användbart uttryck längst ner på pappret (idag 13:52). Läste du tipse om hur du skall gå vidare, som jag skrev strax under?
Okej tack, ja, ska skriva 2sin(a)cos(a) som sin2(a)
men kan inte ett alternativ vara att använda sig energiprincipen för att få fram y på något sätt och sedan gå vidare därifrån? Så som jag föreslog vidare.
Jag kan inte komma på hur man skulle kunna använda energiprincipen i den hr uppgiften (vilket naturligtvis inte behöver betyda att det är omöjligt).
Smaragdalena skrev:Jag kan inte komma på hur man skulle kunna använda energiprincipen i den hr uppgiften (vilket naturligtvis inte behöver betyda att det är omöjligt).
Okej tusen tack!!


