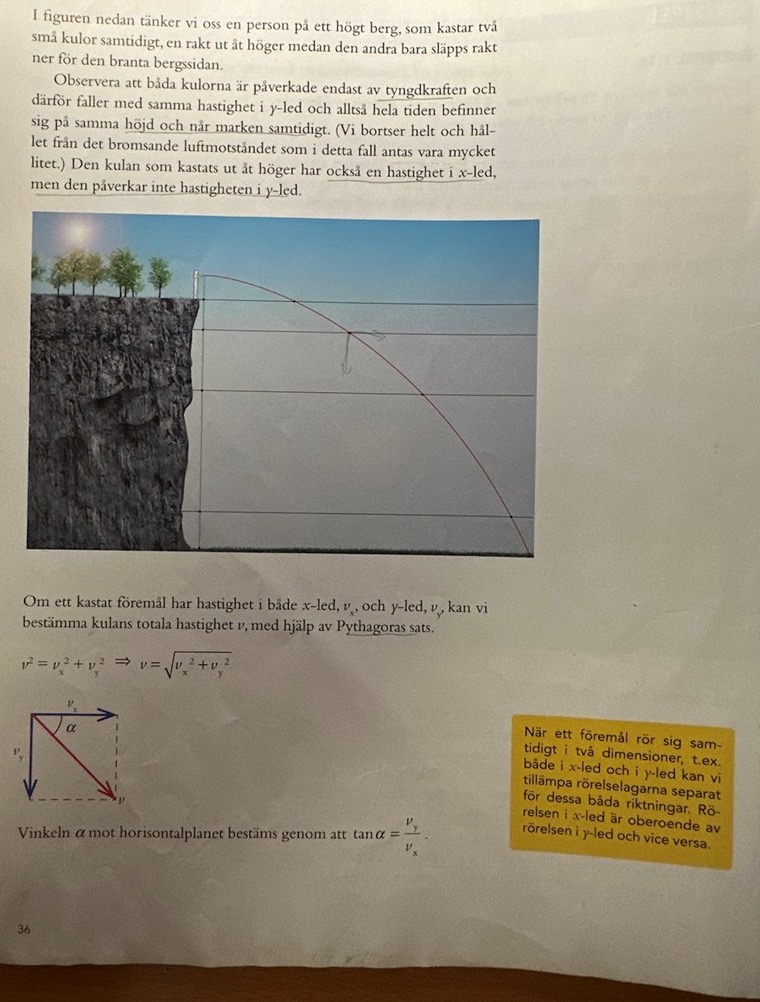
Kaströrelse

För att förenkla problemet begreppsmässigt så skulle jag börja med att införa ett xy-koordinatsystem där origo placeras vid bilens "uthoppspunkt".

Sedan skulle jag beskriva bilens fortsatta färd genom luften med hjälp av en funktion y = f(x) och sluttningen med hjälp av en annan funktion y = g(x).

Sedan skulle jag lösa ekvationen f(x) = g(x) för att få reda på landningspunktens x-koordinat.

Bilen kör rakt fram när den kommer till början av backe. Kaste sker därför i vinkeln 0 grader mot x axeln.

Därför gäller under luftfärden

Vx = 15 => x = 15t

Vy = 0 -gt  => y = -gt*t/2

 backens ekvation ges av

y=-x
 kan du få fram någon lösning med hjälp av det?

Jag förstår Vy = 0 -gt  =>

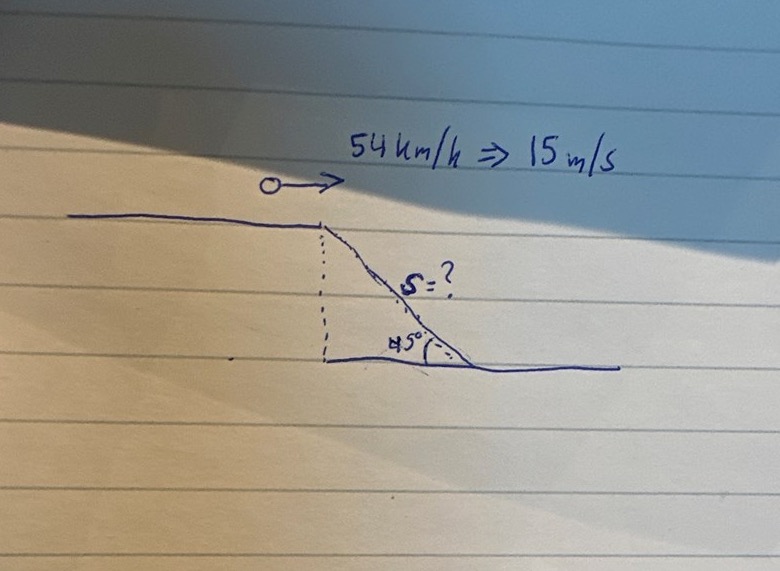
stämmer min figur?

men inte riktigt följande:

y = -gt*t/2

Och backens ekvation ges av

y=-x

Biorr skrev:

Jag förstår Vy = 0 -gt  =>

stämmer min figur?

men inte riktigt följande:

y = -gt*t/2

Och backens ekvation ges av

y=-x

Ja, din figur stämmer, men det är inte tydligt hur du har lagt in koordinatsystemet.

Jag föreslår att du gör så här:

======

För bilen gäller följande:

Eftersom detta är en kaströrelse, dvs "fritt fall"/konstant acceleration så ges bilens x- och y-position generellt av formlerna

• $x(t)=x_0+v_{0x}t+\frac{a_xt^2}{2}$
• $y(t)=y_0+v_{0y}t+\frac{a_yt^2}{2}$

Om du lägger origo vid uthoppspositionen med x-axeln åt höger och y-axeln uppåt som jag föreslog ovan så gäller det att

• Startpositionen i x-led är $x_0=0$ m
• Startpositionen i y-led är $y_0=0$ m
• Starthastigheten i x-led är $v_{0x}=15$ m/s
• Starthastigheten i y-led är $v_{0y}=0$ m/s
• Accelerationen i x-led är $a_x=0$ m/s²
• Accelerationen i y-led är $a_y=-g$

Det ger dig de förenklade positionsformlerna

• $x(t)=15t$
• $y(t)=-\frac{gt^2}{2}$

Säg till om du vill att vi förklarar detta närmare.

=========

För backen gäller att den kan ses som en rät linje (egentligen en stråle) med lutning -45° (dvs riktningskoefficient -1) och som breder ut sig åt höger från origo.

Det betyder att ekvationen för denna räta linje är y = -x.

Säg till om du vill att vi förklarar detta närmare.

========

Om du är med på ovanstående så har du ekvationssystemet 

• $x(t)=15t$
• $y(t)=-\frac{gt^2}{2}$
• $y=-x$

Kommer du vidare då?

Hur gick det med denna, kom du vidare?

Det jag inte förstår är hur dina formler går ihop med de som visas i min lärobok.

Biorr skrev:

Det jag inte förstår är hur dina formler går ihop med de som visas i min lärobok.

I svar #6 visade jag de generella formlerna för läge i x- och y-led vid konstant acceleration.

De formler som står i din bok är förenklade sådana, som förutsätter följande:

• Att startpunkten ligger i origo.
• Att x-axeln är riktad horisontellt i rörelsens riktning.
• Att y-axeln är riktad vertikalt uppåt.
• Att den enda kraft som påverkar föremålet är gravitationen.

Om dessa förutsättningar är uppfyllda så säger formlerna exakt samma sak.

Är det just detta du vill att vi förklarar närmare eller är det något annat, typ varför $v_{0x}=v_0\cdot\cos(\alpha)$?

håller på att repetera fysik 2 uppgifter och detta gjorde mig förvirrad igen.

hur får jag tiden t för hela fallsträckan?

det i parentes var fel

Biorr skrev:

håller på att repetera fysik 2 uppgifter och detta gjorde mig förvirrad igen.

hur får jag tiden t för hela fallsträckan?

[...]

Hängde du med på det jag skrev i #6?

I så fall så hoppas jag att du är med på att bilen landar då $y=-x$.

Detta ger dig ekvationen $-\frac{gt^2}{2}=-15t$, med de två lösningarna $t_1=0$ och $t_2=\frac{30}{g}\approx3,05$ sekunder.

$t_1$ är då bilen far över kanten och  $t_2$ är då den landar.

Att den landar efter cirka 3 sekunder verkar rimligt.

Biorr skrev:

Det är bara den här biten jag inte förstår  :

”

För backen gäller att den kan ses som en rät linje (egentligen en stråle) med lutning -45° (dvs riktningskoefficient -1) och som breder ut sig åt höger från origo.

Det betyder att ekvationen för denna räta linje är y = -x.

Säg till om du vill att vi förklarar detta närmare.”

Hur kan det bli detta ”y = -x.” Är pga koordinaterna (x,y)? 

Biorr skrev:

Det är bara den här biten jag inte förstår  :

”

För backen gäller att den kan ses som en rät linje (egentligen en stråle) med lutning -45° (dvs riktningskoefficient -1) och som breder ut sig åt höger från origo.

Det betyder att ekvationen för denna räta linje är y = -x.

Säg till om du vill att vi förklarar detta närmare.”

 

Hur kan det bli detta ”y = -x.” Är pga koordinaterna (x,y)? 

 

Observera att jag har lagt in koordinatsystemet så att x pekar åt höger och y pekar uppåt. Dvs så som man 'brukar" göra.

Om man i ett sådant koordinatsystem ritar en rät linje y = kx+m, där k = -1 och m = 0 så får man den räta linjen y = -x, dvs den röda grafen:

Denna linje har lutningen -1 , dvs -45°.

Alla punkter (x, y) på denna linje har koordinaterna (x, -x) eftersom y = -x.

Detta gäller även för bilens landningspunkt, dvs då bilen landar så är dess y-koordinat lika med det negativa värdet av dess x-koordinat.

Därav sambandet y_bil = -x_bil då bilen landar.

Svarade det på din fråga?

stämmer mitt resonemang ?

Ja, det stämmer i huvudsak.

Det finns en del saker som inte stämmer och andra saker sm kan förbättras. De påverkar inte slutresultatet, men de kan mycket väl medföra poängavdrag.

Detta text är mer för att göra det lättare för mig att förstå.

Vilka saker stämmer inte och vad kan förbättras?

Saker som inte stämmer:

Här skriver du att s₀ är en sträcka, det borde vara en position.

Sidlängderna i trianglarna stämmer inte. En sidlängd kan aldrig vara negativ. Till höger skriver du att x = -x, vilket inte stämmer.

Även här skriver du att s_X och s_Y avser sträckor, det borde vara positioner.

Saker som kan förbättras:

Här skriver du "vinkeln mellan vinkeln v₀ och x-axeln", men v₀ är inte en vinkel.

Du svarar med 3 värdesiffror, du borde avrunda till 2 värdesiffror och skriva $\approx$ istället för = i svaret.