Kaströrelse - Fel lösning
Hej! Jag var på sista steget i min lösning innan GeoGebra visade en error. Ser däremot inte felet i lösningen. Uppskattar om någon hade kunnat hjälpa mig 🙏🏼 Tusen tack på förhand.
Tror att rätt lösning ska inkludera lösning av t, men förstår inte varför min lösning inte kan vara korrekt.

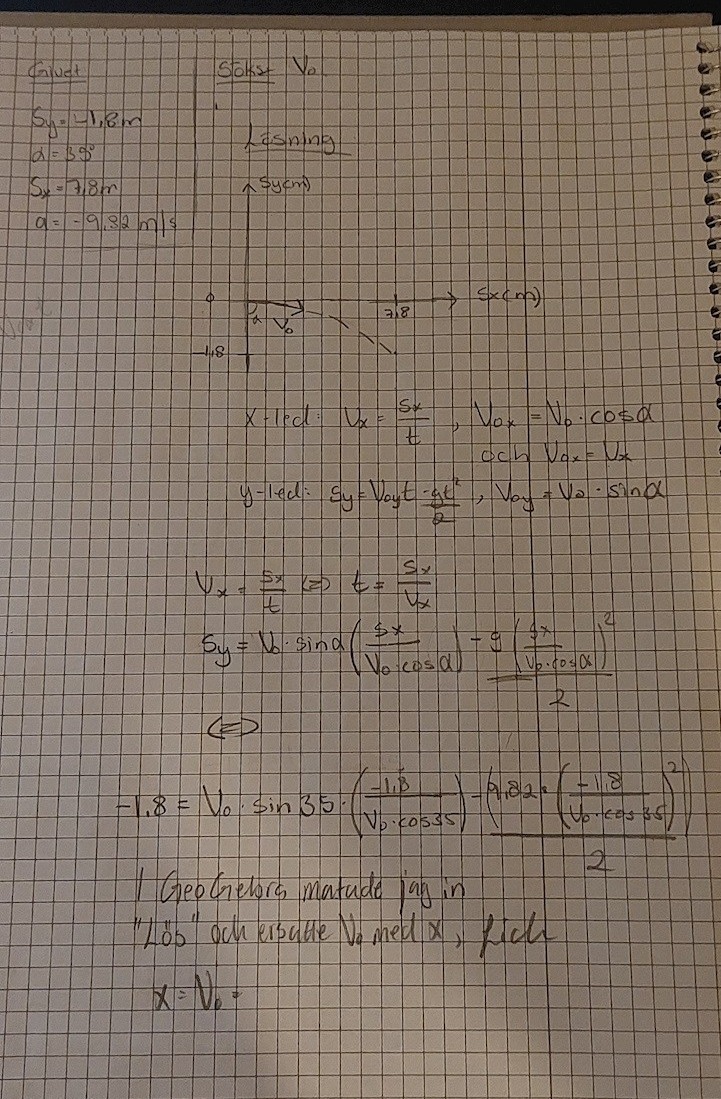
Hej.
Ett fel är att du har ersatt sx med -1,8 meter. Det borde vara 7,8 meter.
Ett annat är att du har ritat bilden lite fel. Kulan stöts snett uppåt med vinkeln mot horisontalplanet, inte mot vertikalpöanet som du har ritat.
Men enligt formeln handlar det om sy eller har jag fel?
Här har du ersatt sx med -1,8:

Är det inte sy som ska stå där? 😅 sy = -1.8 m
Formeln är
Eftersom du väljer att lägga in koordinatsystemet så att origo ligger vid utkastpositionen och att positiv y-riktning är uppåt så får du att och att .
Det ger dig
====
Du vet att hastigheten i x-led är konstant, nämligen
Du vet att kulan landar vid m.
Eftersom så får vi att tidpunkten då kulan landar är
=====
Y-positionen då kulan landar får vi alltså genom
Byt nu ut mot , mot 35°, mot 7,8 och mot -1,8 så får du
Ur detta kan du lösa ut
Dr.scofield skrev:Är det inte sy som ska stå där? 😅 sy = -1.8 m
Korta svaret är nej. Om det står sx så kan du inte bara byta ut det mot sy.
Tack så mycket för hjälpen! Har även ritat om koordinatsystemet, undrar om den nya skissen ser korrekt ut? 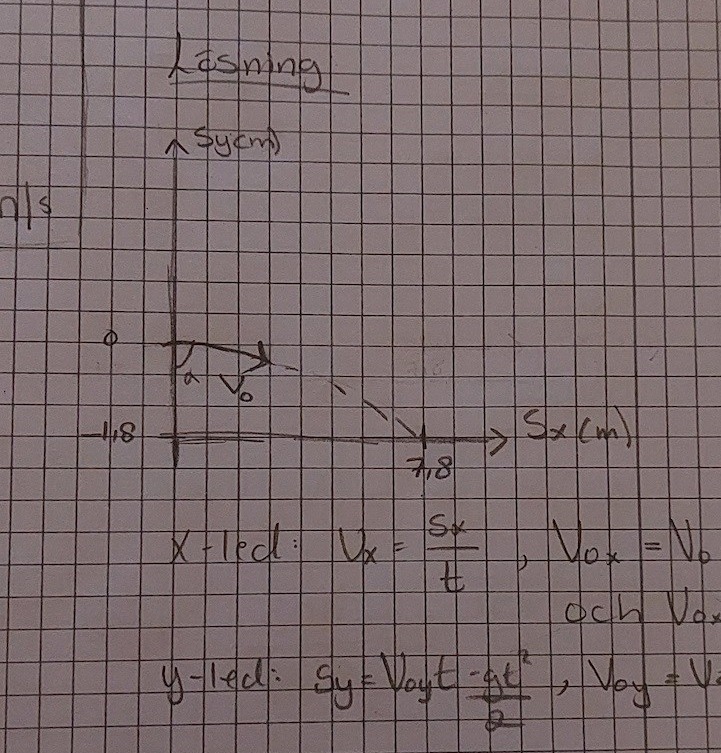
Om du stöter kula, eller kastar en boll för den delen, så är jag säker på att du helt naturligt siktar lite uppåt mot himlen.
Du kastar inte bollen rakt fram dit näsan pekar om du vill komma så långt som möjligt.
Justerade din skiss en aning:
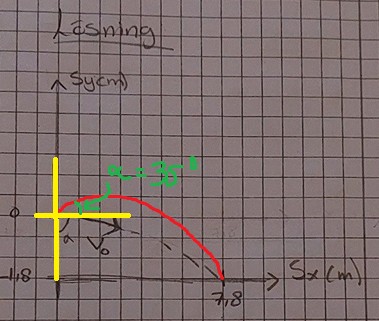
Jaha då förstår jag! Jag fick dessutom fel värde på V0 när jag satte in det i GeoGebra. Min ekvation blev:

Jag ser nu att jag skrivit helt fel på slutet i svar #6.
Den sista termen ska vara
Du har skrivit -1,8 istället för 7,8 i täljaren här:

Tack för all hjälp! :)



